Вивід рівняння регресії: Розглянемо дві випадковості величини X та Y. Нехай для кожного значенню X знайдеться декілька значень величини Y:
x1=2 → y1=6;y2=8;y3=10.
Середнє арифметичне значення величини Y при X=xi називається умовним середнім і позначаться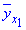 
. В нашому випадку має
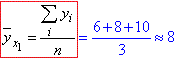
Якщо залежність X від Y є кореляційною залежністю, то умовна середня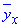 
функціонально залежить від X:
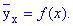(1)
Рівняння (1) називається рівнянням регресії Y по X;
f(x) регресія Y на X, а її графік – лінія регресії Y на X.
Аналогічно визначається кореляційна залежність X від Y:
xy=g(y). (2)
Нехай X та Y – дві випадкові величини, зв'язані кореляційною залежністю. Для знаходження рівняння цієї залежності проводять n незалежних експериментів, в результаті отримують n пар чисел:
(x1;y1),(x2;y2),…,(xn;yn) (3)
Множина пар (3) є вибірковою з генеральної сукупності всіх можливих пар (x;y) значень X та Y.
Розподіл вибірки (3) називається вибірковим розподілом пари випадкових величин X та Y.
Рівняння (1), визначене за даними вибірки (3) називається вибірковим рівнянням регресії Y на X.
Знайдемо вибіркове рівняння регресії (1) по вибірці (3) у вигляді лінійного рівняння.
Будемо вважати, що задані середні значення величини Y для кожного значення X.
Розглянемо лінійну функцію:
y=kx+b. (4)
Рівняння (4) називається прямою лінією регресії Y на X. Кутовий коефіцієнт прямої лінії регресії Y на X називається вибірковим коефіцієнтом регресії Y на X і позначається ρyx. Тоді (4) можна переписати у вигляді.
y'=ρyx•x+b. (5)
Якщо y'i=ρyx•xi+b, а yi- спостережувальне значення Y, яке відповідає xi, то різницю y'i-yi називають відхиленням значень Y. Підберемо параметри ρ=ρyx та b так, щоб сума квадратів відхилень F(ρ,b) яка рівна
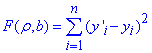
або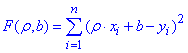 
(6)
була мінімальною.
В цьому і полягає метод найменших квадратів.
Для знаходження мінімуму прирівняємо до нуля відповідні частинні похідні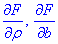 
по ρ та b.
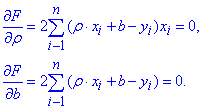
Враховуючи, що ρ та b константи, перепишемо систему рівнянь у вигляді (7)
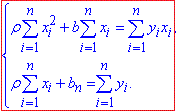
Звідси маємо формули для обчислення коефіцієнтів рівняння прямої регресії
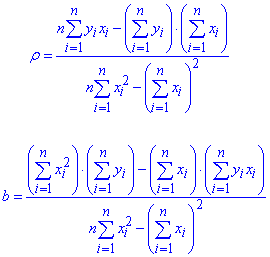
І саме рівняння прямої регресії
y= ρ•x+b (11)
На практиці, як правило, обчислюють складові, що входять в систему лінійних рівнянь 7 (СЛАР).
Далі, розв'язок СЛАР ρ, b підставляють в рівняння регресії.
Приклади на рівняння регресії Y на X
Приклад 1. Знайти вибіркове рівняння прямої лінії регресії Y на X за даними n=5 спостережень:
xi | 1 | 2 | 3 | 4 | 5 |
yi | 3 | 5 | 4 | 6 | 8 |
Розв'язання: Знайдемо спочатку середні значення
∑xi=1+2+3+4+5=15
∑yi=3+5+4+6+8=26
∑xi•yi=1•3+2•5+3•4+4•6+5•8=89
∑xi^2=1^2+2^2+3^2+4^2+5^2=55
Використовуючи систему рівнянь (7) знайдемо ρ та b:
{55 ρ +15b=89; 15ρ +5b=26}
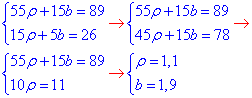
Запишемо вибіркове рівняння прямої лінії регресії Y на X:
y=1,1x+1,9.
Щоб візуалізувати, для чого ми проводимо ці всі розрахунки наведемо рівняння прямої регресії та таблиці значень (X,Y) в математичному пакеті Мейпл
> restart;with(plots):
>q1:=plot([[1,3],[2,5],[3,4],[4,6],[5,8]],x=0..5.5,style=point,symbol=circle,color=blue):
q2:=plot(1.1*x+1.9,x=0..5.5):
display(q1,q2);
В результаті отримаємо
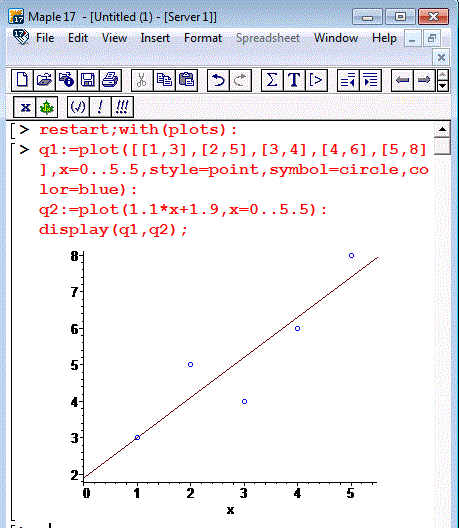
Відповідь: y=1,1x+1,9.
Є завдання коли для одного значення xi маємо кілька значень yi і навпаки, але про них піде мова дальше. Формально задача одна і та ж, побудувати рівняння прямої регресії Y на X. При цьому коефіцієнти прямої слід підбирати так, щоб сума найменших квадратів між прямою і точками була мінімальною.
