Якщо ймовірність p появи події A в окремому випробуванні близька до нуля p<<0,1, то навіть при відносно невеликих n кількостях випробувань значення ймовірністі, обчислюване за локальною теоремою Лапласа виявляється недостатньо точним. В таких випадках використовують формулу виведену Пуассоном.
ТЕОРЕМА ПУАССОНА
Якщо ймовірність p настання події A в кожному випробуванні постійна, але достатньо мала p<<0,1, число незалежних випробувань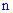 
достатньо велике, при цьомувиконується 
то ймовірність того, що в n випробуваннях подія A наступить рівно k разів приблизно рівна
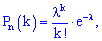- формула Пуассона
де ""лямда" рівна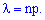 
Для формули Пуассона використовують таблиці табулювань функції Pn(k).
Приклади на формулу Пуассона
Приклад 1. Автобіографія письменника видається тиражем в 1000 екземплярів. Для кожної книжки ймовірність бути неправильно зброшурованою рівна 0,002. Знайти ймовірність того, що тираж міститиме рівно 7 бракованих підручників.
Розв'язання. Перевіримо виконання умов теореми Пуассона. Для вхідних даних
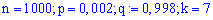
отримаємо,
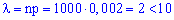
що умови теореми виконуються.
За значеннями функції Пуассона знаходимо ймовірність
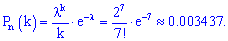
Застосуємо до цієї події локальну теорему Лапласа
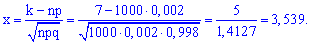
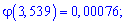
та визначимо ймовірність
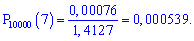
Точне значення імовірності дає формула Бернуллі
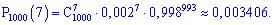
З аналізу трьох методів слідує, що формула Пуассона дає точніше наближення, ніж формула Лапласа. Саме тому її рекомендують застосовувати для відшукання ймовірності в такого сорту задачах.
Приклад 2. Ймовірність виготовлення нестандартної деталі рівна 0,002. Знайти ймовірність того, що серед 1000 деталей виявиться 5 нестандартних.
Розв'язання. Для даних задачі n=1000, p=0,004 виконуються вимоги теореми Пуассона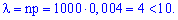 
За таблицею функції Пуассона при k=5 отримаємо:
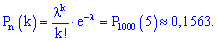
Знайдемо ймовірність тієї ж події за локальною теоремою Лапласа.
Маємо n=1000, p=0,004, k=5.
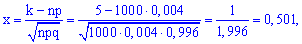
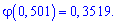
Шукана ймовірність рівна 0,1763
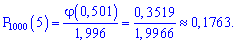
Точне значення надає формула Бернулі:
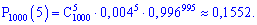
Таким чином, у даному випадку формула Пуассона дає набагато більш точне наближення, ніж формула Лапласа, яка загалом випадає з діапазону.
Приклад 3. Верстат штампує деталі. Ймовірність того, що виготовлена деталь бракована, дорівнює 0,02. Яка ймовірність того, що серед 200 деталей виявиться 5 бракованих?
Розв'язання. Маємо значення n=200, p=0,02, k=5, які задовільняють вимоги теореми
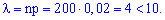
За таблицею функції Пуассона при k=5 одержимо наступне значення ймовірності:
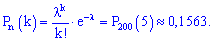
Приклад 4. Фабрика випускає в середньому 0,4% нестандартних виробів.
Яка ймовірність того, що число нестандартних виробів у партії з 1000 штук буде 15?
Обчислення: Переведемо відсотки вибрати нестандартний виріб в ймовірність
p=0,4%/100%=0,004.
Партія n=1000 штук, звідси λ=n•p=1000•0,004=4<10, тому для знаходження ймовірності скористаємося теоремою Пуассона
P1000(15)= λ^15•exp(λ)/15!.
Враховуючи раніше знайдене "ламбда» виконуємо обчислення
P1000(15)= 4^15•2,718^4/15!=0,04483
Відповідь: 0,04483.
На цьому коротка практика завершена.
Використовуйте формулу Пуассона в тих завданнях, де вона більш доречна. Завжди перевіряйте виконання умови теореми Пуассона, при значеннях, які не задовольняють умову n*p<10 формула дає велику похибку при обчисленні ймовірності. Для перевірки результату застосовуйте формулу Бернуллі, вона більш точна і з її результатом знайдену ймовірність за формулою Пуассона краще всього порівнювати. Якщо похибка невелика, тоді Ви все зробили правильно, в іншому випадку доведеться обчислювати знову або знайти слабке місце і виправити помилки.
