Скалярний та векторний добутки. Проекція вектора на вектор

В даній статті будуть дані основні інструкції, щодо векторів. З їх допомого Ви будете знати що з ними можна робити, а що ні. Тож переходимо до вивчення операцій над векторами.
І. Сумою двох -вимірних векторів
і називають -вимірний вектор , координати якого дорівнюють сумі відповідних координат векторів - доданків, тобто

Для прикладу, якщо ,
то
З цього правила випливає, що різницею двох векторів буде вектор, координати якого є різницею відповідних координат векторів.

ІІ. Добутком числа (скаляра) на -вимірний вектор називається -вимірний вектор , координати якого дорівнюють добутку числа на відповідні координати вектора ,тобто

Для прикладу,

Операції додавання векторів та множення числа на вектор ( - деякі числа) володіють властивостями:
1)
2)
3)
4)
5)
6)
7) Для довільного вектора існує протилежний вектор такий, що

ІІІ. Скалярним добутком двох -вимірних векторів і називають число, що дорівнює сумі добутків відповідних координат векторів, тобто

Для прикладу,
якщо , то

Згідно іншого означення, скалярний добуток двох векторів це число, яке рівне добутку довжин векторів (їх модулів) на косинус кута між ними

З наведеного вище означення можна отримати формулу для обчислення кута між векторами

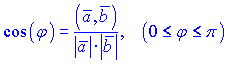
або в координатній формі

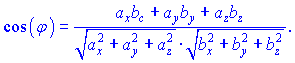
Також є формулювання згідно якого, скалярний добуток двох векторів рівний модулю одного з них помноженому на проекцію другого вектора на напрям першого

З останнього означення випливають формули, для знаходження проекції вектора на вектор

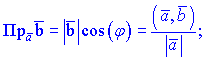
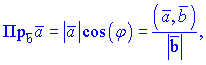
або в координатній формі

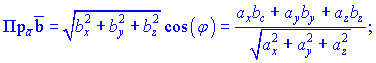
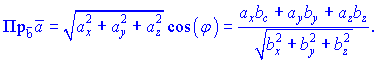
Приклади знаходження скалярного добутку, кута між векторами та проекції одного вектора на інший будуть розглянуті нижче.

Алгебраїчні властивості скалярного добутку векторів:

1)
2)
3)
4)Рівність має місце за умови

Геометричні властивості скалярного добутку

1) вектори перпендикулярні між собою, якщо

2) кут між векторами гострий у випадках, коли

3) кут між векторами тупий у випадках, коли

ІV. Векторним добутком або двох векторів називається вектор , який відповідає наступним умовам:
1) модуль вектора рівний добутку модулів векторів і на синус кута між ними

2) вектор нормальний до площини, побудованої на векторах і ;
3) вектор напрямлений так, що з його кінця найкоротший поворот від вектора до відбувається проти руху годинникової стрілки. Іншими словами, вектори утворюють праву трійку.

Векторний добуток має наступні геометричні властивості:
Його модуль рівний площі паралелограма побудованого на векторах і

Тому площа трикутника, побудованого на векторах і рівна модулю половини векторного добутку цих векторів

Алгебраїчні властивості векторного добутку

1) векторний добуток рівний нулю у випадку колінеарності векторів та коли один з них нульовий;
2) від перестановки векторів векторний добуток змінює знак на протилежний:

3)
4)

На практиці важливо мати під рукою формулу для обчислення векторного добутку в координатній формі, тому запишемо і її

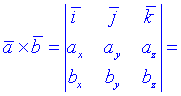
Розглянемо конкретні приклади для засвоєння пройденого матеріалу.

Приклад 1. Задано вектори та
Знайти наступні величини
1) суму векторів
2) скалярний добуток векторів
3) векторний добуток площу трикутника побудованого на векторах
4) кут між векторами
5) проекцію кожного з векторів на інший

Розв'язок. 1) Проведемо обчислення

2) Скалярний добуток буде рівний

3) Векторний добуток обчислюємо згідно формули

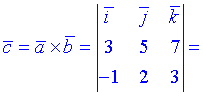
Площа трикутника буде рівна

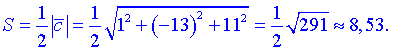
4) Знайдемо кут між векторами за

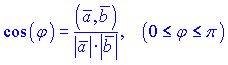
У ній скалярний добуток вже знайдений, тож знаходимо довжини векторів

Підставляємо потрібні значення у формулу

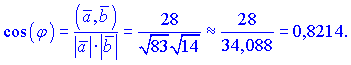
Знаходимо значення кута

5) Знайдемо проекції векторів

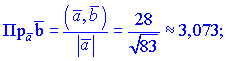
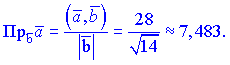
Проекції векторів можна шукати через косинус кута між векторами, результат від цього не зміниться

На цьому урок закінчено. Вивчайте правила та властивості операцій над векторами, вони стануть Вам у нагоді при навчанні.