Властивості sin(x), cos(x),tg(x), ctg(x)

Наведені та структуровані основні характеристики тригонометричних функцій sin(x), cos(x), tg(x), ctg(x), які є вкрай необхідними при дослідженні графіків та поведінки цих функцій, спрощенні тригонометричних виразів, обчисленні рівнянь та нерівностей.
Основну частину присутніх тут формул Ви повинні вміти легко застосовувати на практичних, а для цього частину матеріалу потрібно завчити та знати.
Це не стосується всіх формул, але частину основних тригонометричних тотожностей, а також формули синуса чи косинуса подвійного кута слід запам'ятати. 

Cинус y=sin(x)  

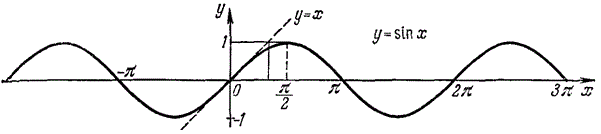
Область визначення:    D(y): x∈R
Область допустимих значень:    E(y):y∈[-1;1], тобто  -1≤sin(x)≤1.
Функція непарна:         sin(-a)=sin(a).
Функція періодична з найменшим додатним періодом 2Pi: sin(a+2Pi)=sin(a).
Точки перетину з осями координат: (0,0) на осі Oy; (Pi·k;0), k∈Z на осі Ox.
Проміжки знакопостійності:
y>0, якщо x∈(2Pi·k;Pi+2Pi·k), k∈Z;  
y<0, якщо x∈(Pi+2Pi·k;2Pi+2Pi·k),  k∈Z.
Проміжки зростання: [-Pi/2+2Pi·k; Pi/2+2Pi·k], k∈Z, звідси y_max=1 у точках  x_max=Pi/2+2Pi·k.
Проміжки спадання:  [Pi/2+2Pi·k; 3Pi/2+2Pi·k], k∈Z, звідси y_min=-1 у точках  x_min=-Pi/2+2Pi·k.                   

Косинус y=cos(x)

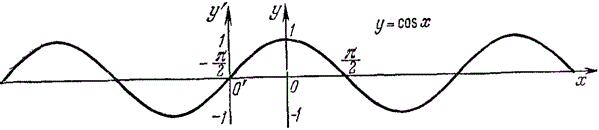
Область визначення: D(y): x∈R
Область значень:       E(y):y∈[-1;1], тобто  -1≤cos(x)≤1.
Функція парна:          cos(-a)=cos(a).
Функція періодична з найменшим додатним періодом 2Pi: cos(a+2Pi)=cos(a).
Точки перетину з осями координат: (0;1) на осі Oy, (Pi/2+Pi·k;0), k∈Z на осі Ox;
Проміжки знакопостійності:
y>0, якщо x∈(-Pi/2+2Pi·k;Pi/2+2Pi·k), k∈Z;
y<0, якщо x∈(Pi/2+2Pi·k;3Pi/2+2Pi·k), k∈Z.
Проміжки зростання: [Pi+2Pi·k; 2Pi·k], k∈Z, звідси  y_max=1  у точках  x_max= 2Pi·k.
Проміжки спадання:  [2Pi·k; Pi+2Pi·k], k∈Z,   звідси  y_min=-1 у точках   x_min= Pi+2Pi·k.             

Тангенс y=tg(x)

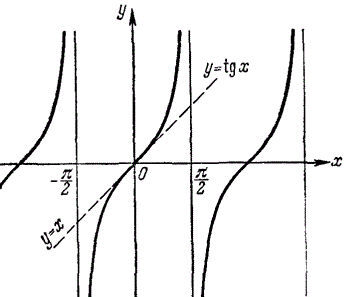
Область визначення: D(y):x≠Pi/2+Pi·k, k∈Z;
Область значень:      E(y): y∈R, тобто  -∞≤tg(x)≤+∞.
Функція непарна       tg(-a)=-tg(a).
Функція періодична з найменшим додатним періодом Pi:  tg(a+Pi)=tg(a).
Точки перетину з осями координат: (0;0) на осі Oy;  (Pi·k;0), k∈Z  на осі Ox.
Проміжки знакопостійності:
y>0, якщо x∈(Pi·k;Pi/2+Pi·k), k∈Z;
y<0, якщо x∈(-Pi/2+Pi·k; Pi·k), k∈Z .
Проміжки зростання: (-Pi/2+Pi·k; Pi/2+Pi·k), k∈Z.
Найменших і найбільших значень функція не має .  

Котангенс y=ctg(x)

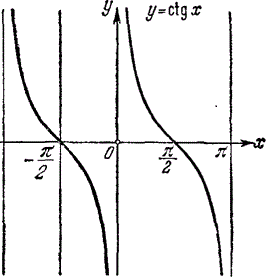
Область визначення: D(y):x≠ Pi·k, k∈Z;
Область значень:      E(y): y∈R, тобто  -∞≤ctg(x)≤+∞.
Функція непарна       ctg(-a)=-ctg(a).
Функція періодична з найменшим додатним періодом Pi: ctg(a+Pi)=ctg(a).
Точки перетину з осями координат:
не перетинає вісь Oy;
(Pi/2+Pi·k;0), k∈Z на осі Ox
Проміжки знакопостійності:
y>0, якщо x∈(Pi·k;Pi/2+Pi·k), k∈Z;
y<0, якщо x∈(Pi/2+Pi·k;Pi+Pi·k), k∈Z.
Проміжки спадання: (Pi·k;Pi+Pi·k), k∈Z.
Найменших і найбільших значень функція не має.  

Значення тригонометричних функцій для деяких кутів:

Формули зведення:

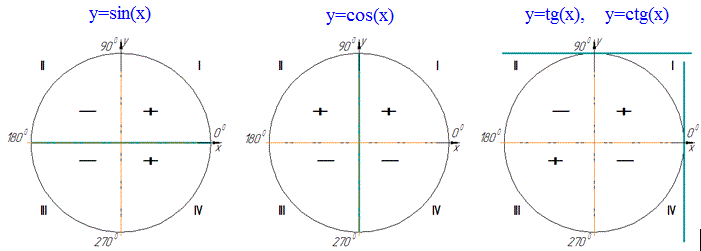
Знаки тригонометричних функцій:

Зв'язок між тригонометричними функціями одного аргументу:

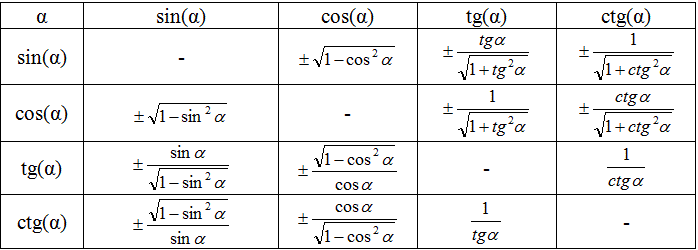
 У наведених формулах перед знаком радикала слід взяти знак «плюс» або «мінус»
залежно від того, в якій чверті лежить кут α саме так, щоб знак тригонометричної
функції, який стоїть у лівій частині збігався зі знаком величини, що стоїть у правій
частині рівності.   

Основні тригонометричні тотожності

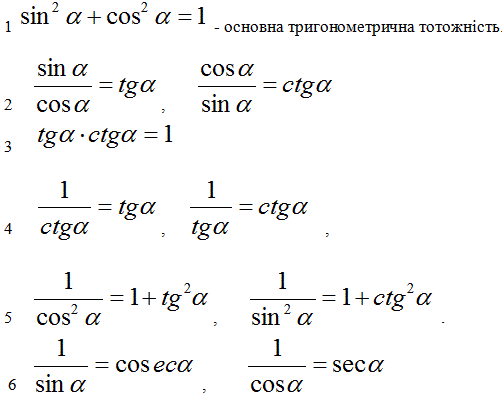
Універсальна тригонометрична підстановка

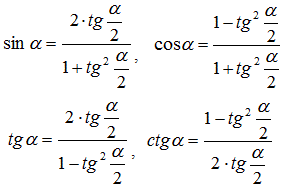
Тригонометричні функції суми і різниці аргументів

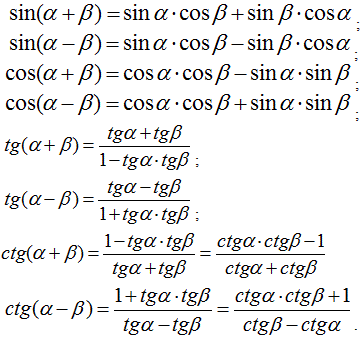
Тригонометричні функції подвійного, потрійного і половинного
       аргументів

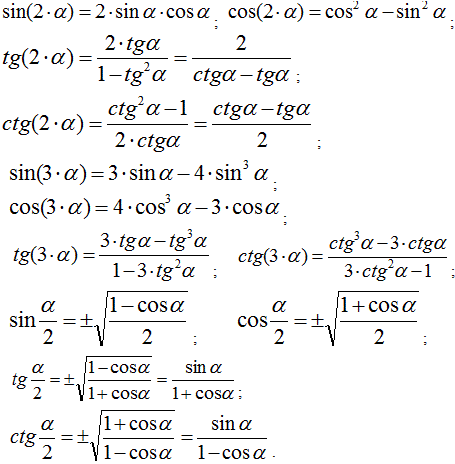
Перетворення суми тригонометричних функцій у добуток

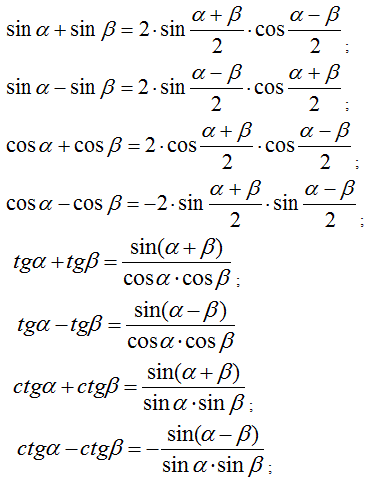
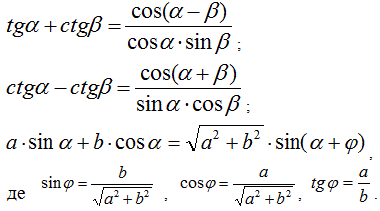
Перетворення добутку тригонометричних функцій у суму

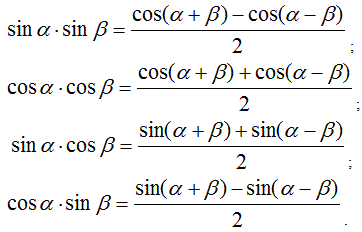
Далі будуть наведені відповіді до поширених на практиці прикладів з тригонометрії на знаходження значень тригонометричних виразів, розв'язування рівнянь та нерівностей на яких буде показано всю силу наведених вище формул.