Складні тригонометричні рівняння

Переходимо до пояснення розв'язків складних тригонометричних рівнянь. Тут маємо приклади де аргумент в тригонометричній функції знаходиться під коренем або в квадраті, також рівняння де аргумент або сама функція містяться під модулем. Кожен з прикладів вимагає іншого підходу при зведенні рівнянь до найпростішого типу. Водночас на подібних прикладах Ви швидко навчитеся розписувати складні завдання та знатимете яку зі схем застосовувати.
При підготовці до зовнішнього незалежного оцінювання наведені далі приклади часто мало кому вдалося вирішити правильно, тож для абітурієнтів наведені відповіді також стануть в нагоді при вступі до ВУЗ-ів.
Для перевірки правильності обчислень можете скористатися графічним методом та програмами, описаними на попередніх уроках.

Приклад 18.13 Розв'язати рівняння cos²(x)+5cos(x)-6=0.

Розв'язання: З вигляду тригонометричного рівняння робимо висновок, що через заміну змінних його слід звести до квадратного рівняння.
Зробимо заміну cos(x)=t, причому змінна має відповідати області визначення косинуса -1≤t≤1.
В такий спосіб прийдемо до квадратного рівняння t²+5t-6=0.
За теоремою Вієта знаходимо: t1=1 і t2=-6<-1 (не задовольняє умові).
Отже, отримали cos(x)=1, звідси корінь рівний

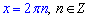
Відповідь: Д.

Приклад 18.14 Розв'язати рівняння sin(x)+cos(x)=-√2.

Розв'язання: Подамо вираз sin(x)+cos(x) у вигляді добутку:

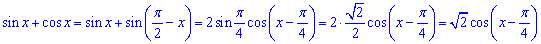
Отже, отримали рівняння

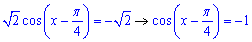
звідси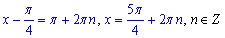
Але якщо 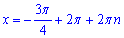, то отримаємо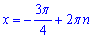
(Оскільки ).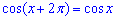
Відповідь: В.

Приклад 18.15 Розв'язати рівняння sin(x²)=0.

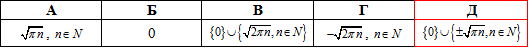
Розв'язання: Аргумент під синусом міститься в другому степені, тому з правої частини потрібно буде знаходити корінь квадратний.
Запишемо розв'язок рівняння

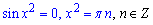
звідси 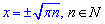, а також 0, оскільки раніше номер пробігав множину цілих чисел (тепер натуральних).
Остаточно отримаємо множину коренів

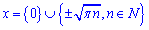
Відповідь: Д.

Приклад 18.16 Розв'язати рівняння tg(√x)=-1.

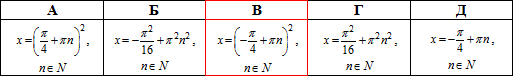
Розв'язання: Тангенс розкриваємо за допомогою оберненої тригонометричної функції – арктангенса

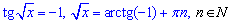
Тут навмисне відкинули від'ємні номери серед цілих, оскільки корінь від'ємним бути не може.
Далі переходимо до кутів

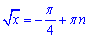
та підносимо до квадрата обидві частини

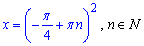
Відповідь: В.

Приклад 18.17 У якому вигляді можна подати розв'язок рівняння cos(Pi•x)=x2-4x+5?

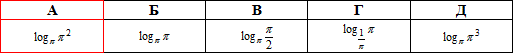
Розв'язання: Почнемо з аналізу ОДЗ:

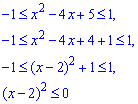
Звідси слідує, що рівняння має корені, якщо x=2.
Серед тестових відповідей такого значення немає, тому штучно вводимо логарифм за основою Пі від Пі, щоб привести 2 до однієї з відповідей
Відповідь: А.

Приклад 18.18 Розв'язати рівняння cos(cos(x))=1.

Маємо косинус від косинуса в лівій частині та одиницю в правій.
Розкриваємо зовнішній косинус

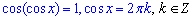
Далі виписуємо обмеження на ОДЗ внутрішнього косинуса

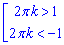
при 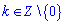(без нуля).
Потрібних номерів k щоб виконувались нерівності немає, тому розглянемо єдиний випадок:
k=0, тоді cos(x)=0, звідси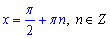
Відповідь: Б.

Приклад 18.19 Розв'язати рівняння sin(x)+sin(|x|)=0.

Розв'язання: Маємо тригонометричне рівняння з синусами, один з аргументів в якому взятий по модулю.
Для обчислень замінюємо наведене р-ня системою рівнянь для різних значень аргументу

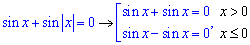
Далі рівняння розв'язуємо:

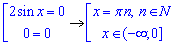
Сукупність розв'язків заданого рівняння має вигляд:

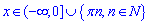
Відповідь: Г.

Приклад 18.20 Розв'язати рівняння |cos(x)|=cos(x)+2sin(x).

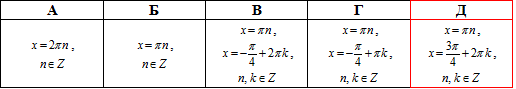
Розв'язання: Маємо тригонометричне рівняння з модулем косинуса, яке за методикою замінюємо еквівалентною системою тригонометричних рівнянь вже без модулів, але з певними обмеженнями на підмодульну функцію.
В даному випадку матимемо 2 рівняння для від'ємних та додатних (з нулем) значень косинуса.

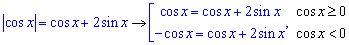
Після спрощення система набуде вигляду

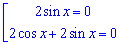
Друге рівняння перетворюємо з врахуванням періодичності косинуса та формули зведення для суми синусів

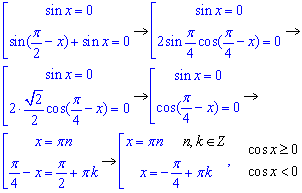
Враховуючи умови розкриття модуля, отримаємо такі корені

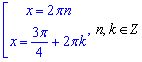
Відповідь: Д.

Приклад 18.35 Розв'язати рівняння sin(Pi•sin(x))=-1.
У відповідь записати кількість коренів на проміжку [0;Pi].
Розв'язання: Маємо складне тригонометричне рівняння з двома вкладеними синусами:
sin(Pi•sin(x))=-1, звідси Pi•sin(x)=-Pi/2+2Pi•n, n∈ Z.
Спрощуємо на Пі
sin(x) )=-1/2+2•n, n∈ Z.
З ОДЗ записуємо умову -1≤ -1/2+2n≤1, з якої отримаємо -1/2≤ 2n≤3/2, або -1/4≤ n≤3/4.
Оскільки n∈ Z (ціле число), то єдиний номер, який задовольняє нерівності n=0.
При ньому останнє рівняння набуде вигляду:
sin(x)=-1/2, звідси

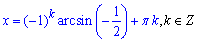
Після підстановки арксинуса

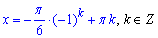
записуємо
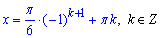- загальний розв'язок заданого рівняння.
Випишемо (і порахуємо їх) усі корені, що належать проміжку [0,Pi]:
при k=-2: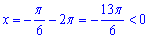
при k=-1: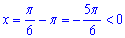
при k=0: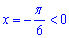
при k=1: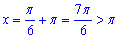
при k=2: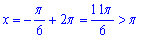
при k≤0 отримаємо x<0;
при k>0 отримаємо x>Pi.
Як бачимо усі корені заданого рівняння знаходять поза межами інтервалу, тому маємо 0 коренів, що належать [0;Pi].
Відповідь: 0.

З цієї статті Ви, мабуть побачили, що не такі вже й складні наведені приклади. Також багатьом з Вас перегляд відповідей допоможе правильно оформляти та аргументувати пояснення при перетворенні та розв'язанні рівнянь.
Тригонометричні рівняння з параметром почнемо аналізувати в наступній статті.