Метод Крамера та Гауса одні з найпоширеніших при обчисленні систем рівнянь третього порядку.
Далі будуть наведені відповіді до поширених прикладів, та окремо розібрані випадки коли СЛАР не мають розв'язків або мають їх безліч.
Приклад 1 Розв'язати систему лінійних алгебраїчних рівнянь
8x1+6x2+5x3=21;
3x1+3x2+2x3=10;
4x1+2x2+3x3=8.
двома способами
- за правилом Крамера
- за методом Гауса
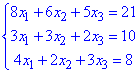
Розв'язання: 1) Розв'яжемо систему рівнянь за правилом Крамера.
Знайдемо визначник головної матриці
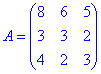
та допоміжні визначники – утворюються заміною відповідних стовпців матриці стовпцем вільних членів.
Визначники розкладаємо через алгебраїчні доповнення до елементів 1 стовпця матриці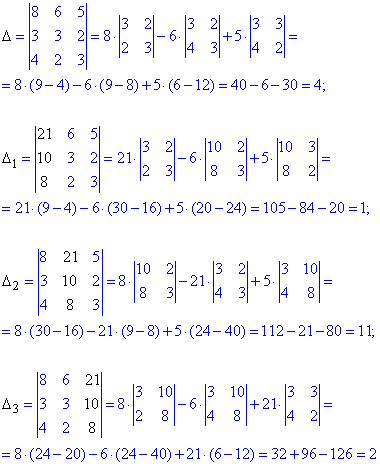
Такий спосіб допомагає швидше знайти ділянку, де допущена помилка при обчисленні детермінанту. В правилі трикутників набагато важче знайти місце, де помилково взято протилежний знак чи підставлено неправильне число. Тому і Вам раджу для матриць 3х3 і вищих порядків шукати визначники через розклади
За формулами Крамера знайдемо розв'язки системи рівнянь: Отож, маємо
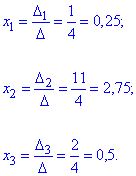
Виконаємо перевірку математичним калькулятором YukhymCalc. Визначники в формулах Крамера знаходимо за правилом трикутників
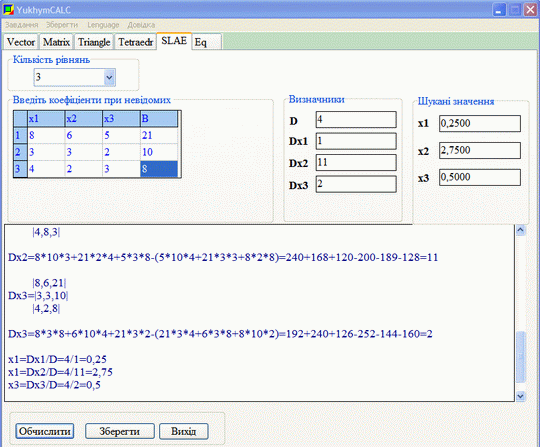
Значення, що знайшли x1=0,25; x2=2,75; x3=0,5 співпадають із тими, що визначені калькулятором, отже помилки при обчисленні визначників відсутні. Завантажуйте та користуйтеся програмою для самоперевірки.
2) Розв'яжемо систему лінійних алгебраїчних рівнянь методом Гауса. За допомогою елементарних перетворень зведемо розширену матрицю
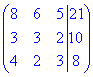
до трикутного (східчастого) виду :
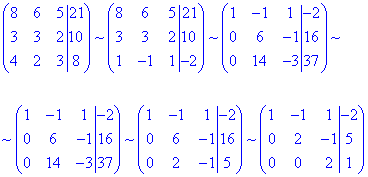
Тут детально не розписували як міняли рядки місцями та шо на шо множили.
У Вас будуть свої завдання, а елементарні перетворення детально розписані в окремій статті.
Звідси отримаємо еквівалентну систему рівнянь:
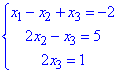
з якої знаходимо розв'язки
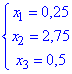
Як можна переконатися розв'язки обох методів співпали, що свідчить про правильність розв'язання системи лінійних алгебраїчних рівнянь.
Приклад 2 Розв'язати двома способами – 1) за правилом Крамера та 2) за методом Гауса – систему лінійних алгебраїчних рівнянь:
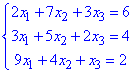
Розв'язання: 1) Спершу виконуємо обчислення за правилом Крамера. Знайдемо визначник головної матриці:
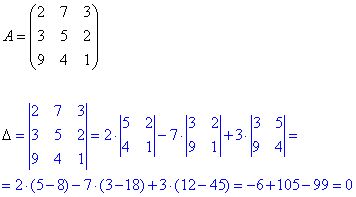
Він рівний нулю, отже (за теоремою Крамера) система лінійних алгебраїчних рівняння має безліч розв'язків (або не має їх взагалі).
2) Розв'яжемо систему рівнянь методом Гауса. Зведемо розширену матрицю
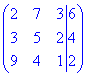
до трикутного (східчастого) виду
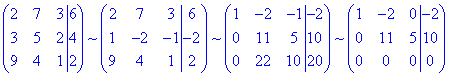
Оскільки в розширеній матриці за допомогою еквівалентних перетворень отримали нульовий рядок, то система лінійних алгебраїчних рівнянь має безліч розв'язків.
Приклад 3 Знайти розв'язок систему лінійних алгебраїчних рівнянь
2x1-3x2+5x3=1;
4x1-6x2+2x3=2;
2x1-3x2-11x3=1.
двома способами – 1) за правилом Крамера та 2) за методом Гауса :
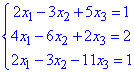
Розв'язання: 1) Розв'яжемо систему рівнянь за правилом Крамера.
Знайдемо визначник матриці:
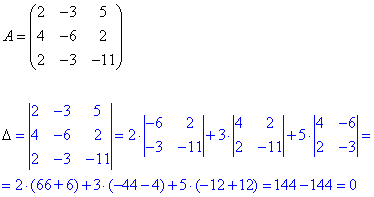
Оскільки визначник рівний нулю (detA=0), то (за теоремою Крамера) система лінійних алгебраїчних рівняння має безліч розв'язків (або не має їх взагалі). 2) Розв'яжемо систему рівнянь методом Гауса. Зведемо розширену матрицю
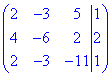
до трикутного (східчастого) виду (за допомогою елементарних перетворень матриці):
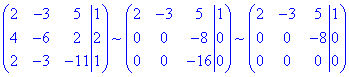
Оскільки в розширеній матриці за допомогою еквівалентних перетворень отримали нульовий рядок, то система лінійних алгебраїчних рівнянь має безліч розв'язків.
Приклад 4 Розв'язати систему лінійних алгебраїчних рівнянь методом Крамера
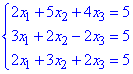
Розв'язання: Розв'яжемо систему рівнянь за правилом Крамера – знайдемо визначник головної матриці та допоміжних.
Для спрощення розрахунків виконаємо розклад через елементарні перетворення до елементів першого стовпця
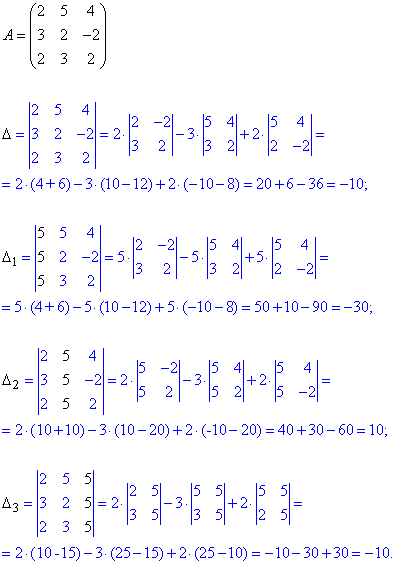
Далі застосовуємо формули Крамера
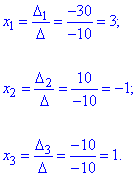
Отже значення x1=3, x2=-1, x3=1 є розв'язками заданої СЛАР.
Виконаємо перевірко калькулятором YukhymCalc
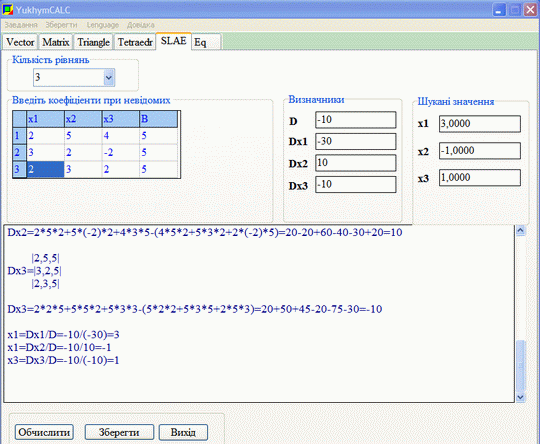
Відповіді x1=3, x2=-1, x3=1 ідентичні, отже попередні обчислення виконані коректно.
Приклад 5 Розв'язати двома способами – 1) за правилом Крамера та 2) за методом Гауса – систему лінійних алгебраїчних рівнянь:
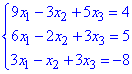
Розв'язання: 1) Розв'яжемо систему рівнянь за правилом Крамера. Знайдемо визначник матриці:
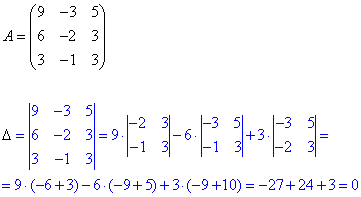
Оскільки визначник рівний нулю, то (за теоремою Крамера) система лінійних алгебраїчних рівняння має безліч розв'язків (або не має їх взагалі).
2) Розв'яжемо систему рівнянь методом Гауса. Зведемо розширену матрицю
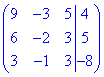
до трикутного (східчастого) виду (за допомогою елементарних перетворень матриці):
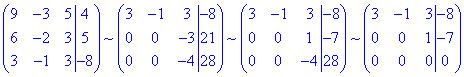
Оскільки в розширеній матриці за допомогою еквівалентних перетворень отримали нульовий рядок, то система лінійних алгебраїчних рівнянь має безліч розв'язків.
Перевірка калькулятором показує, що головний та допоміжні визначники в методі Крамера рівні нулю
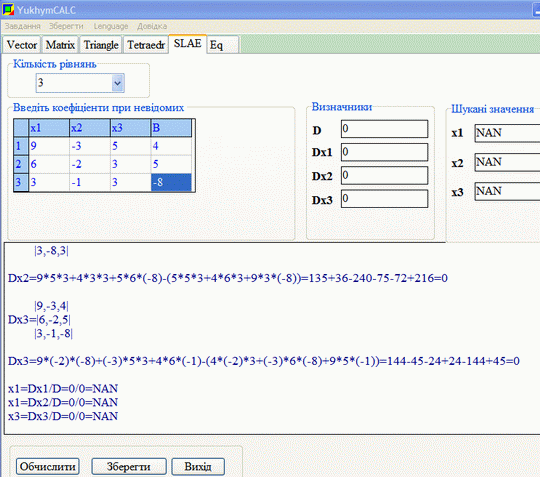
Проте коренів програма не дає, оскільки маємо ділення на нуль.
Ось так просто можна знайти корені системи рівнянь третього порядку двома поширеними методами.
Як знайти розв'язки СЛАР матричним метод та Жордана-Гауса детально розписано в наступних уроках.


