Нехай маємо систему N лінійних алгебраїчних рівнянь (СЛАР) з N невідомими x1, x2,..., xN.,коефіцієнтами при яких є елементи матриці A(aij), а вільними членами є числа b1, b2,..., bN.
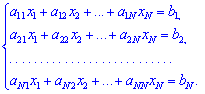
Позначимо через X – матрицю-стовпець невідомих, через B– матрицю-стовпець вільних членів. Тоді попередню систему рівнянь можна записати у вигляді матричного рівняння:
A*X=B
Якщо квадратна матриця A має відмінний від нуля визначник
Враховуючи, що добуток оберненої матриці на саму матрицю дає одиничну
X=A-1*B
Знаходження матричного розв'язку називається матричним способом розв'язування системи лінійних алгебраїчних рівнянь (СЛАР).
Приклад 1. Розв'язати систему лінійних рівнянь матричним методом.
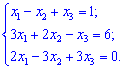
Розв'язок. Маємо систему з трьох рівнянь. Позначимо матрицю і вектори літерами
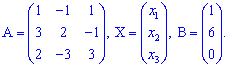
Матричний розв'язок системи алгебраїчних рівнянь шукаємо за формулою X=A-1*B. Для знаходження оберненої матриці A-1 обчислимо визначник
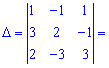
![]()
Оскільки він відмінний від нуля ![]() , то задана система рівнянь сумісна і має єдиний розв'язок.
, то задана система рівнянь сумісна і має єдиний розв'язок.
Знайдемо транспоновану матрицю A
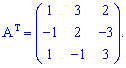
Обчислимо алгебраїчні доповнення до елементів заданої матриці:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Обернену матрицю отримаємо за формулою
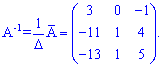
Знайдемо розв'язок СЛАР
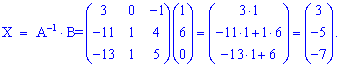
Розв'язок системи рівнянь x1=3; x2=-5; x3=-7.
Розрахунки для системи із трьох рівнянь достатньо прості і зводяться на практиці до обчислень оберненої матриці, що теж не складно. У випадку системи чотирьох рівнянь обчислень буде куда більше і для визначення оберненої матриці доведеться шукати 16 визначників матриць розміром 3x3. Для системи рівнянь 5 порядку при визначенні оберненої матриці необхідно знаходити 25 визначників 4 порядку, або методом розкладу куда більше визначників 3 порядку. Перемножити обернену матрицю на праву частину рівняння після всіх операцій досить просто, і з цим справляються усі. Труднощі лише у обчисленні обернених матриць!
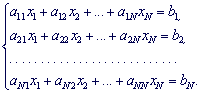
Перший індекс i біля коефіцієнтів aij вказує, в якому рівнянні знаходиться коефіцієнт, а другий j при якому із невідомих він знаходиться.
Якщо визначник матриці A не дорівнює нулю
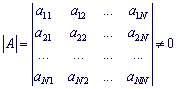
то система лінійних алгебраїчних рівнянь має єдиний розв'язок.
Розв'язком системи лінійних алгебраїчних рівнянь називається така впорядкована сукупність N чисел
Якщо праві частини всіх рівнянь системи дорівнюють нулю, то систему рівнянь називають однорідною. У випадку коли деякі з них відмінні від нуля – неоднорідною
Якщо система лінійних алгебраїчних рівнянь має хоч один розв'язок, то вона називається сумісною, в іншому випадку – несумісною.
Якщо розв'язок системи єдиний, то система лінійних рівнянь називається визначеною. У випадку, коли розв'язок сумісної системи не єдиний, систему рівнянь називають невизначеною.
Дві системи лінійних рівнянь називаються еквівалентними (або рівносильними), якщо всі розв'язки однієї системи є розв'язками другої, і навпаки. Еквівалентні (або рівносильні ) системи отримуємо з допомогою еквівалентних перетворень.
Еквівалентні перетворення СЛАР
1) переставлення місцями рівнянь;
2) множення (або ділення) рівнянь на відмінне від нуля число;
3) додавання до деякого рівняння іншого рівняння, помноженого на довільне, відмінне від нуля число.
Розв'язок СЛАР можна знайти різними способами. Розглянемо найпопулярніші методи.
МЕТОД КРАМЕРА
ТЕОРЕМА КРАМЕРА. Якщо визначник ![]() системи N лінійних алгебраїчних рівнянь з N невідомими відмінний від нуля
системи N лінійних алгебраїчних рівнянь з N невідомими відмінний від нуля ![]() , то ця система має єдиний розв'язок, який знаходиться за формулами Крамера:
, то ця система має єдиний розв'язок, який знаходиться за формулами Крамера:
![]()
![]() - визначники, утворений із
- визначники, утворений із ![]() заміною j-го стовпця, стовпцем із вільних членів.
заміною j-го стовпця, стовпцем із вільних членів.
Якщо ![]() , а хоча б один з
, а хоча б один з ![]() відмінний від нуля, то СЛАР розв'язків немає. Якщо ж
відмінний від нуля, то СЛАР розв'язків немає. Якщо ж ![]() , то СЛАР має безліч розв'язків. Розглянемо приклади з застосуванням методу Крамера.
, то СЛАР має безліч розв'язків. Розглянемо приклади з застосуванням методу Крамера.
Приклад 1. Дано систему трьох лінійних алгебраїчних рівнянь з трьома невідомими. Розв'язати систему за формулами Крамера.
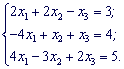
Розв'язок. Знайдемо визначник матриці коефіцієнтів при невідомих.
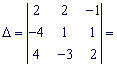
![]()
Так як ![]() , то задана система рівнянь сумісна і має єдиний розв'язок. Обчислимо визначники:
, то задана система рівнянь сумісна і має єдиний розв'язок. Обчислимо визначники:
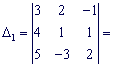
![]()
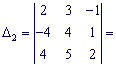
![]()
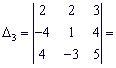
![]()
За формулами Крамера знаходимо розв'язок системи рівнянь
![]()
Отже x1=1; x2=3; x3=5 єдиний розв'язок системи.
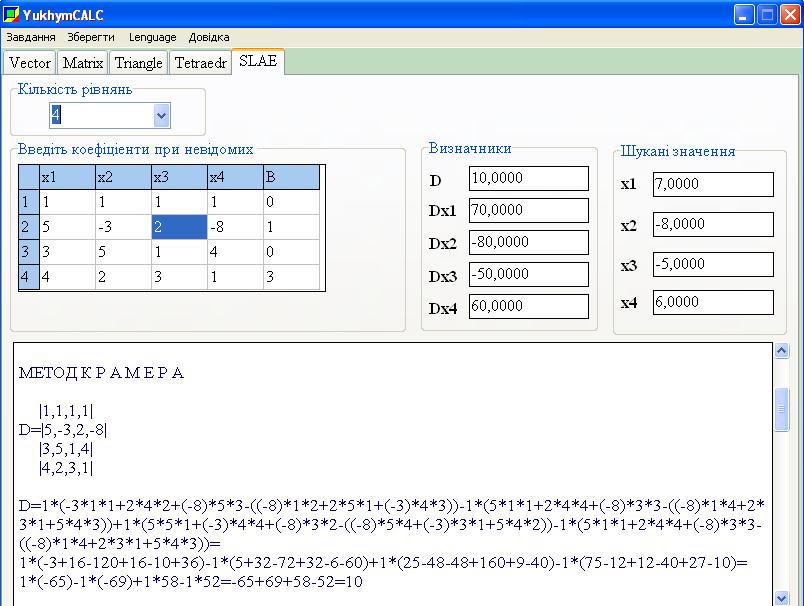
Приклад 2. Дано систему чотирьох лінійних алгебраїчних рівнянь. Розв'язати систему за формулами Крамера
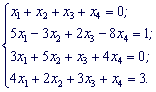
Розв'язок. Знайдемо визначник головної матриці системи. Для цього розкладемо його за першим рядком.
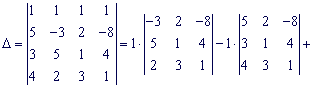
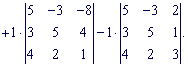
Знайдемо визначники третього порядку
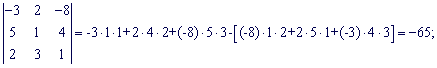
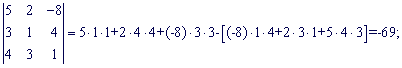
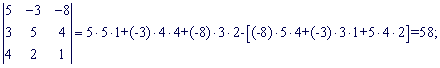
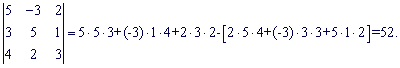
Підставимо знайдені значення у головний визначник
![]()
Визначник матриці не рівний нулеві ![]() , отже система рівнянь сумісна і має єдиний розв'язок. Шукаємо визначники за формулами Крамера
, отже система рівнянь сумісна і має єдиний розв'язок. Шукаємо визначники за формулами Крамера
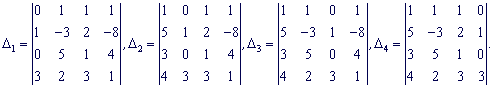
Розкладемо кожен з визначників через стовпець віьних членів, в ньому найбіьше нулів (2).
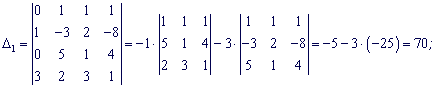
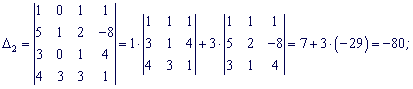
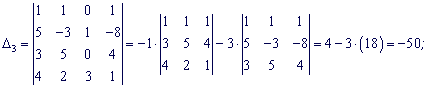
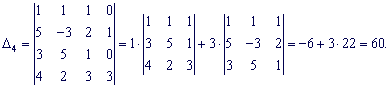
За формулами Крамера обчисюємо корені
![]()
Розв'язок системи x1=7; x2=-8; x3=-5; x4=6.
Даний приклад можна розв'язати програмою YukhymCalc . Фрагмент програми та результати обчислень системи рівнянь наведені нижче.
В результаті розв'язування системи лінійних рівнянь 4 поряду у тестовий файл Ви можете записати наступну відповідь.
МЕТОД КРАМЕРА
|1,1,1,1|
D=|5,-3,2,-8|
|3,5,1,4|
|4,2,3,1|
D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10
|0,1,1,1|
Dx1=|1,-3,2,-8|
|0,5,1,4|
|3,2,3,1|
Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70
|1,0,1,1|
Dx2=|5,1,2,-8|
|3,0,1,4|
|4,3,3,1|
Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80
|1,1,0,1|
Dx3=|5,-3,1,-8|
|3,5,0,4|
|4,2,3,1|
Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50
|1,1,1,0|
Dx4=|5,-3,2,1|
|3,5,1,0|
|4,2,3,3|
Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60
x1=Dx1/D=70,0000/10,0000=7,0000
x2=Dx2/D=-80,0000/10,0000=-8,0000
x3=Dx3/D=-50,0000/10,0000=-5,0000
x4=Dx4/D=60,0000/10,0000=6,0000
Думаю, що Ви захочете мати такого помічника в себе на коп'ютері. Окрім наведених обчислень калькулятор має багато корисних функцій для роботи з матрицями, але це вже не відноситься до системи рівнянь.
]]>
до трикутного (східчастого) вигляду
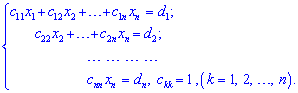
Припустимо, що в системі коефіцієнт при першому елементі відмінний від нуля
За допомогою першого рівняння виключимо x1 із решти рівнянь.
Для цього ділять перший рядок на a11, позначимо це
Далі від другого рядка віднімаємо перший рядок, помножений на a21; від третього перший рядок, помножений на a31; і так далі до останнього рядка.
Дістанемо таблицю коефіцієнтів:

Для невідомих x2, .., xn маємо систему n-1 рівнянь. Виконуючи, як і раніше, виключимо x2 з усіх рівнянь, починаючи з третього. Для цього спочатку поділимо другий рядок на ![]() .
.
Якщо коефіцієнт ![]() , то переставимо рівняння так, щоб виконувалася умова
, то переставимо рівняння так, щоб виконувалася умова ![]() . Позначивши
. Позначивши
![]() ,
,
від третього рядка віднімемо другий рядок, помножений на ![]() ;
;
від четвертого рядка віднімемо другий рядок, помножений на ![]() і т.д.
і т.д.
Дістанемо таблицю коефіцієнтів:

Продовжуючи процес виключення невідомих отримаємо

таблицю коефіцієнтів при невідомих, яка має вигяд верхньої трикутної матриці. Всі елементи на головній діагоналі рівні одиниці ![]() . Запишемо відповідну систему рівнянь:
. Запишемо відповідну систему рівнянь:
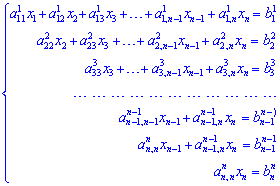
Перехід від першої системи рівнянь до останньої називається прямим ходом методу Гауса. Обернений хід методу Гауса починається з останньої системи рівнянь. Її розв'язують з кінця до початку. З останнього рівняння знаходять xn. Підставивши це значення в передостаннє – знаходять xn-1 і т.д. З першого рівняння знаходять x1.
Якщо система рівнянь з N невідомими має єдиний розв'язок, то ця система завжди може бути перетворена до трикутного вигляду. Для студентів не завжди вимагають, щоб діагональні елементи були рівні одиниці. Достатньо просто звести систему лінійних рівнянь до верхньої трикутної.
Приклад 1. Дано систему трьох лінійних алгебраїчних рівнянь з трьома невідомими. Розв'язати систему методом Гаусса.
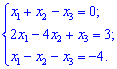
Розв'язок. Виключимо невідому x1 з другого і третього рівняння. Для цього від них віднімемо перше помножене на 2; 1:
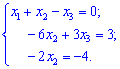
Бачимо, що наше рівняння в такому вигляді можна розв'язувати оберненим ходом методу Гауса. Для цього з останнього рівняння виразимо x2
![]()
Підставимо отримане значення в попереднє рівняння і знайдемо x3
![]()
З першого рівняння знаходимо x1
![]()
Розв'язок даної системи рівний x1 =3; x2=2; x3=5.
У випадках систем великих розмірів, а також для зручності, часто на практиці використовують іншу схему розв'язування. Замість перетворень над системою виконують відповідні перетворення над матрицею, складеною з коефіцієнтів при невідомих і стовпця з вільних членів, який для зручності виокремлюють вертикальною лінією. Таку матрицю ![]() називають розширеною матрицею системи.
називають розширеною матрицею системи.
Приклад 2. Розв'язати систему чотирьох лінійних алгебраїчних рівнянь методом Гаусса.
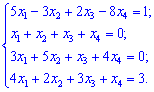
Розв'язок. Випишемо розширену матрицю для даної системи
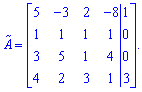
Зведемо її до трикутного вигляду з допомогою елементарних перетворень.
1. Поміняємо місцями перший і другий рядки.
2. Додамо до елементів другого, третього і четвертого рядків елементи першого рядка, помножені відповідно на -5; -3; -4.
3. Поміняємо місцями другий і третій рядки. Додамо до елементів третього і четвертого рядків елементи другого рядка, помножені відповідно на 4;1.
4. Від четвертого рівняння помноженого на 11 віднімаємо третє рівняння помножене на -3.
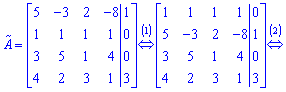
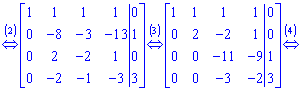
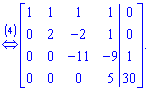
Такій розширеній матриці відповідає наступна система рівнянь
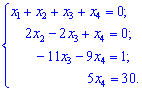
З четвертого рівняння знаходимо 4 невідому ![]() і підставляємо в третє рівняння
і підставляємо в третє рівняння
![]()
Знайдені значення підставляємо в друге рівняння
![]()
З першого рівняння знаходимо першу невідому
![]()
Системо повністю розв'язана і x1 =7; x2=-8; x3=-5; x4=-6 – її розв'язок.
Користуйтеся схемою Гауса де це вимагає умова завдання і використовуйте приведені схеми розрахунків.
Для початку виберемо завдання із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Розв'язати систему лінійних алгебраїчних рівнянь.
1) (1. 153) 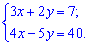
Розв'язок. У випадку двох рівнянь розв'язок можна отримати простішим способом. Виразимо з другого рівняння x
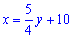
та підставимо у перше
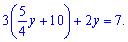
Розкривши дужки, згрупуємо подібні доданки
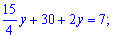
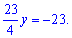
Звідси отримаємо розв'язок y=-4.
Змінну x знайдемо підстановкою y у будь-яке із рівнянь
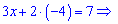
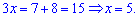
Таким чином розв'язком системи двох рівнянь будуть значення x=3; y=-4.
Оскільки мета статті навчити студентів розв'язувати методом Крамера, то розв'яжемо даний приклад і ним.
Для цього випишемо систему лінійних рівнянь у вигляді
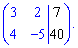
Знайдемо детермінант основної частини
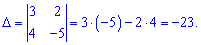
Для обчислення допоміжних визначників ставимо стовпець вільних членів на місце першого рядка для 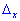 та на місце другого для
та на місце другого для 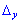 . В результаті отримаємо
. В результаті отримаємо
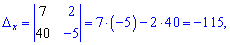
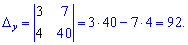
Підставимо знайдені значення в формули Крамера
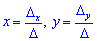
та знайдемо невідомі
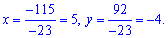
З розглянутого прикладу видно, що обчислення при двох рівняннях з двома невідомими досить прості.
Далі будуть наведені обчислення для систем іх трьох рівнянь.
2) (1. 165)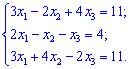
Розв'язок. Запишемо систему трьох рівнянь у зручному для розв'язування вигляді
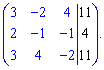
Знайдемо детермінант системи за правилом трикутників
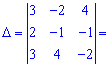
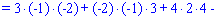
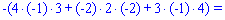
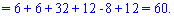
Для знаходження додаткових визначників підставляємо стовпець вільних членів на місце першого, другого та третього стовпців. В результаті прийдемо до детермінантів
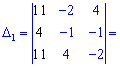
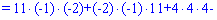
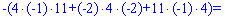
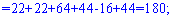
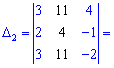
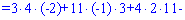
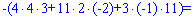
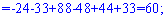
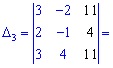
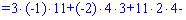
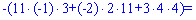
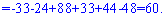
Обчислюємо невідомі за формулами Крамера
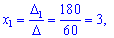
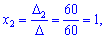
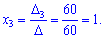
Для даної системи рівнянь знаходження розв'язку теж не надто складно, хоча в порівнянні з системою двох рівнянь обчислень помітно прибавилося.
3) (1. 174) 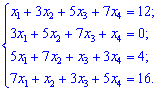
Розв'язок. Перетворимо систему рівнянь четвертого порядку до вигляду

Знаходимо головний визначник системи. При обчисленні детермінантів четвертого порядку їх вартує розкладати за рядками чи стовпцями в яких найбільше нулів. Оскільки, в даному випадку нулів головний визначник немає, то розкладемо його за першим рядком
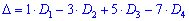
та знайдемо відповідні детермінати третього порядку
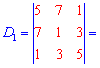
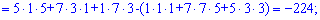
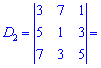
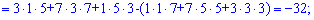
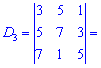
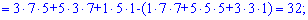
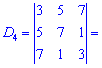
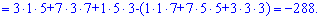
Підставимо знайдені значення у визначник
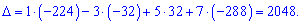
За такою ж схемою обчислюємо допоміжні визначники, нагадаю лише, що вони утворюються заміною стовпця у головному визначнику на стовпець вільних членів (позначений чорним кольором). Я не проводитиму детальних розписувань всіх розрахунів, проте Ви можете перевірити, що детермінанти приймуть значення
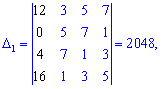
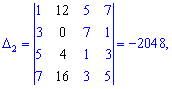
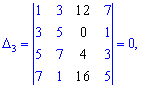
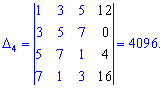
Підставивши в формули Крамера, після обчислень отримаємо x1=1; x2=-1; x3=0; x4=2
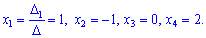
На цьому завдання розв'язано. Системи чотирьох лінійних рівнянь найбільш трудомісткі в обчисленнях, для визначення їх розв'язку потрібно обчислювати 5*4=20 визначників третього порядку, в той час як системи трьох рівнянь лише 4. Будьте уважні при обчисленнях, адже найменша помилка може мати наслідком неправильний результат.
Нульовий розв'язок
x1=0;x2=0; ...xn=0
завжди задовольняє однорідну систему рівнянь. Ненульовий розв'язок (якщо він існує) знаходять методом Гауса. Якщо кількість рівнянь і невідомих однакові m=n і головний визначник рівний нулеві
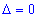 то однорідна система має безліч розв'язків. Кількість залежних розв'язків рівна рангу системи лінійних рівнянь r(A), решта приймають будь-які значення.
то однорідна система має безліч розв'язків. Кількість залежних розв'язків рівна рангу системи лінійних рівнянь r(A), решта приймають будь-які значення.Найчастіше на практичних заняттях зустрічаються системи двох однорідних рівнянь з трьома невідомими та трьох з трьома.
Нехай маємо перший випадок
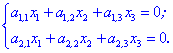
Якщо мінори другого порядку ненульові, то розв'язок можна знайти за формулами
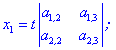
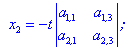
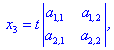
де t
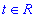 - будь-яке дійсне число.У випадку однорідної системи трьох рівнянь наступного вигляду
- будь-яке дійсне число.У випадку однорідної системи трьох рівнянь наступного вигляду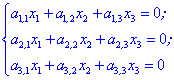
можливі три варіанти:
І. Детермінант рівний нулю 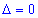 , тоді система має безліч розв'язків.
, тоді система має безліч розв'язків.
ІІ. Коли хоча б один з детермінантів другого порядку відмінний від нуля:
Якщо перший з них відмінний від нуля
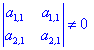
то розв'язки знаходимо за формулами наведеними для двох рівнянь.
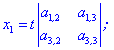
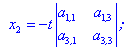
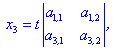
Якщо маємо два ненульові визначнии
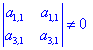
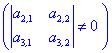
то за формулами
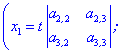
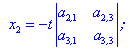
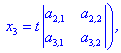
де 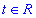 - дійсне число.
- дійсне число.
ІІІ. Якщо і мінори другого порядку рівні нулю, то система зводиться до одного рівняння з трьома невідомими. Надаючи двом невідомим довільних значень знаходять третє.
Розв'яжемо приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика" для закріплення матеріалу на практиці.
Приклад 1. Розв'язати систему рівнянь.
(1. 205) 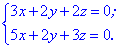
Розв'язок: Маємо однорідну систему з двох рівнянь та трьох невідомих.
Знайдемо визначник другого порядку перших двох стовпців матриці
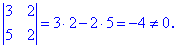
Оскільки він відмінний від нуля то розв'язок знаходимо за правилами
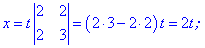
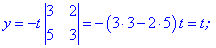
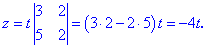
Таким способом отримали наступний результат
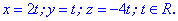
Для двох рівнянь достатньо зрозумілі і прості розрахунки.
Приклад 2. Розв'язати систему рівнянь.
(1.208) 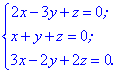
Розв'язок: Дана однорідна система має три рівняння і три невідомі. Спершу обчислимо визначник матриці за правилом трикутників
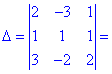
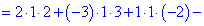
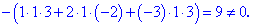
Він приймає ненульове значення. Це дозвояє знайти корені системи рівнянь за форулами
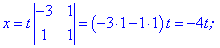
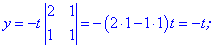
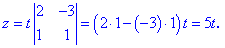
Отримали розв'язок, який заежить від параметра
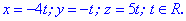
Приклад 3.Знайти розв'язки системи рівнянь.
(1. 213) 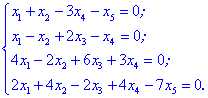
Розв'язок:Маємо однорідну систем з 4 рівнянь з 5 невідомими. Перепишемо рівняння системи так, щоб невідомі знаходилися одні під одними
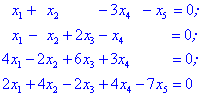
та спростимо систему методом Гауса.
Для цього перетворимо в нуль всі коефіцієнти при x1 після першого рядка
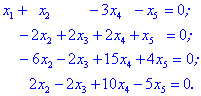
Виключаємо з нижніх рівнянь x2
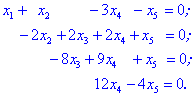
Отримали східчасту систему, яку розв'язуємо з кінця
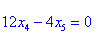
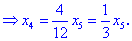
Знайдені корені підставляємо в третє рівняння
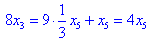
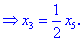
З другого рівняння знаходимо x2
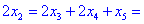
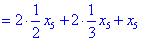
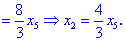
Всі знайдені значення підставляємо в перше рівняння
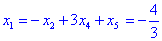
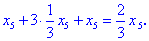
Кінцевий розв'язок однорідної системи матиме вигляд
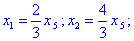
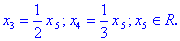
Це рівносильно запису, що x5=t , а всі попередні виражаються через останній, тобто через параметр.
При розв'язуванні однорідних систем лінійних рівнянь вищих порядків метод Гауса є незамінним. При системах другого, третього порядку розв'язати можна швидше за наведеними на початку статті формулами, в порівнянні з методом Гауса. Спробуйте розв'язати подібні приклади самостійно та виберіть для себе зручнішу методику.
Далі будуть наведені відповіді до поширених прикладів, та окремо розібрані випадки коли СЛАР не мають розв'язків або мають їх безліч.
Приклад 1 Розв'язати систему лінійних алгебраїчних рівнянь
8x1+6x2+5x3=21;
3x1+3x2+2x3=10;
4x1+2x2+3x3=8.
двома способами
- за правилом Крамера
- за методом Гауса
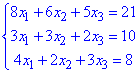
Розв'язання: 1) Розв'яжемо систему рівнянь за правилом Крамера.
Знайдемо визначник головної матриці
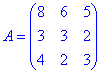
та допоміжні визначники – утворюються заміною відповідних стовпців матриці стовпцем вільних членів.
Визначники розкладаємо через алгебраїчні доповнення до елементів 1 стовпця матриці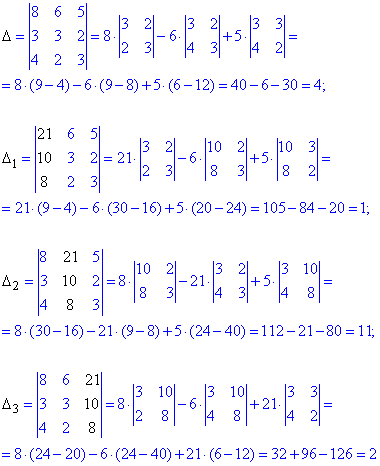
Такий спосіб допомагає швидше знайти ділянку, де допущена помилка при обчисленні детермінанту. В правилі трикутників набагато важче знайти місце, де помилково взято протилежний знак чи підставлено неправильне число. Тому і Вам раджу для матриць 3х3 і вищих порядків шукати визначники через розклади
За формулами Крамера знайдемо розв'язки системи рівнянь: Отож, маємо
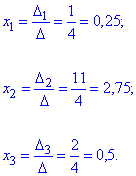
Виконаємо перевірку математичним калькулятором YukhymCalc. Визначники в формулах Крамера знаходимо за правилом трикутників
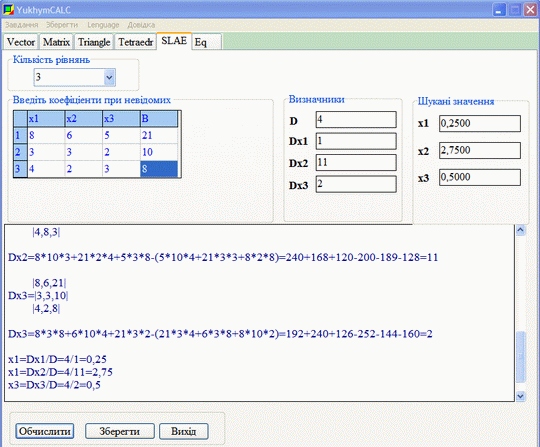
Значення, що знайшли x1=0,25; x2=2,75; x3=0,5 співпадають із тими, що визначені калькулятором, отже помилки при обчисленні визначників відсутні. Завантажуйте та користуйтеся програмою для самоперевірки.
2) Розв'яжемо систему лінійних алгебраїчних рівнянь методом Гауса. За допомогою елементарних перетворень зведемо розширену матрицю
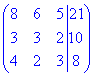
до трикутного (східчастого) виду :
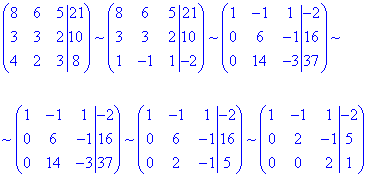
Тут детально не розписували як міняли рядки місцями та шо на шо множили.
У Вас будуть свої завдання, а елементарні перетворення детально розписані в окремій статті.
Звідси отримаємо еквівалентну систему рівнянь:
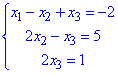
з якої знаходимо розв'язки
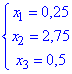
Як можна переконатися розв'язки обох методів співпали, що свідчить про правильність розв'язання системи лінійних алгебраїчних рівнянь.
Приклад 2 Розв'язати двома способами – 1) за правилом Крамера та 2) за методом Гауса – систему лінійних алгебраїчних рівнянь:
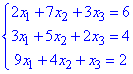
Розв'язання: 1) Спершу виконуємо обчислення за правилом Крамера. Знайдемо визначник головної матриці:
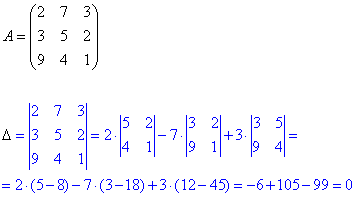
Він рівний нулю, отже (за теоремою Крамера) система лінійних алгебраїчних рівняння має безліч розв'язків (або не має їх взагалі).
2) Розв'яжемо систему рівнянь методом Гауса. Зведемо розширену матрицю
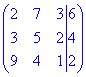
до трикутного (східчастого) виду
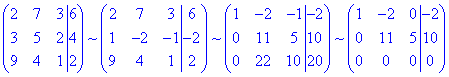
Оскільки в розширеній матриці за допомогою еквівалентних перетворень отримали нульовий рядок, то система лінійних алгебраїчних рівнянь має безліч розв'язків.
Приклад 3 Знайти розв'язок систему лінійних алгебраїчних рівнянь
2x1-3x2+5x3=1;
4x1-6x2+2x3=2;
2x1-3x2-11x3=1.
двома способами – 1) за правилом Крамера та 2) за методом Гауса :
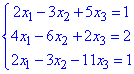
Розв'язання: 1) Розв'яжемо систему рівнянь за правилом Крамера.
Знайдемо визначник матриці:
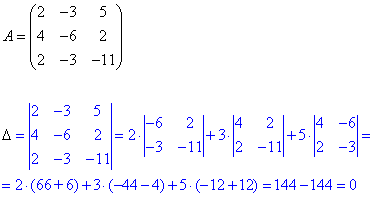
Оскільки визначник рівний нулю (detA=0), то (за теоремою Крамера) система лінійних алгебраїчних рівняння має безліч розв'язків (або не має їх взагалі). 2) Розв'яжемо систему рівнянь методом Гауса. Зведемо розширену матрицю
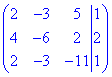
до трикутного (східчастого) виду (за допомогою елементарних перетворень матриці):
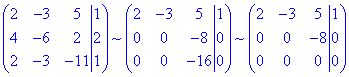
Оскільки в розширеній матриці за допомогою еквівалентних перетворень отримали нульовий рядок, то система лінійних алгебраїчних рівнянь має безліч розв'язків.
Приклад 4 Розв'язати систему лінійних алгебраїчних рівнянь методом Крамера
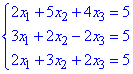
Розв'язання: Розв'яжемо систему рівнянь за правилом Крамера – знайдемо визначник головної матриці та допоміжних.
Для спрощення розрахунків виконаємо розклад через елементарні перетворення до елементів першого стовпця
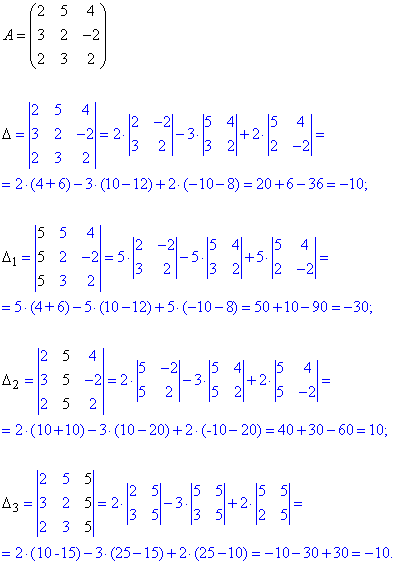
Далі застосовуємо формули Крамера
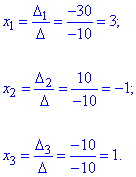
Отже значення x1=3, x2=-1, x3=1 є розв'язками заданої СЛАР.
Виконаємо перевірко калькулятором YukhymCalc
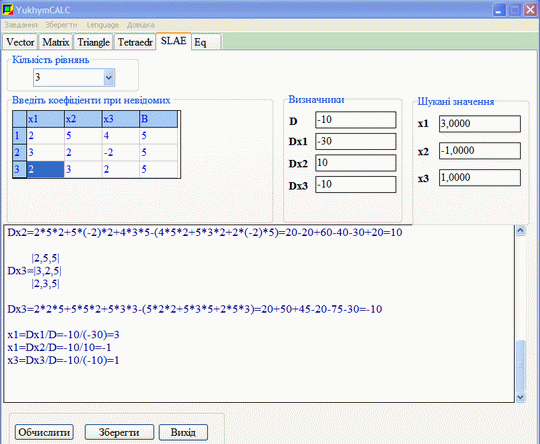
Відповіді x1=3, x2=-1, x3=1 ідентичні, отже попередні обчислення виконані коректно.
Приклад 5 Розв'язати двома способами – 1) за правилом Крамера та 2) за методом Гауса – систему лінійних алгебраїчних рівнянь:
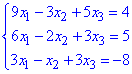
Розв'язання: 1) Розв'яжемо систему рівнянь за правилом Крамера. Знайдемо визначник матриці:
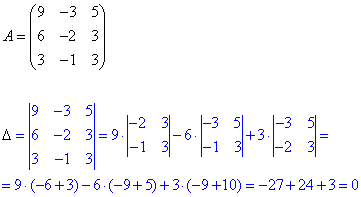
Оскільки визначник рівний нулю, то (за теоремою Крамера) система лінійних алгебраїчних рівняння має безліч розв'язків (або не має їх взагалі).
2) Розв'яжемо систему рівнянь методом Гауса. Зведемо розширену матрицю
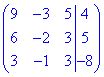
до трикутного (східчастого) виду (за допомогою елементарних перетворень матриці):
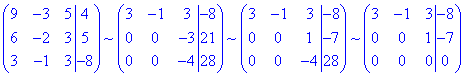
Оскільки в розширеній матриці за допомогою еквівалентних перетворень отримали нульовий рядок, то система лінійних алгебраїчних рівнянь має безліч розв'язків.
Перевірка калькулятором показує, що головний та допоміжні визначники в методі Крамера рівні нулю
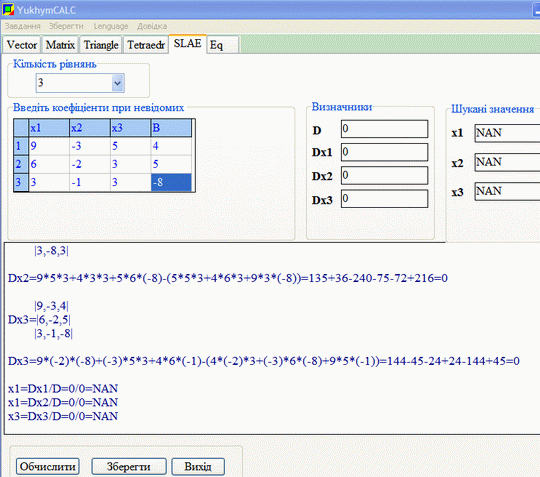
Проте коренів програма не дає, оскільки маємо ділення на нуль.
Ось так просто можна знайти корені системи рівнянь третього порядку двома поширеними методами.
Як знайти розв'язки СЛАР матричним метод та Жордана-Гауса детально розписано в наступних уроках.
Розглянемо приклади розв'язування систем лінійних рівнянь , взявши за довідник збірник задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Розв'язати систему лінійних алгебраїчних рівнянь.
(1. 189) 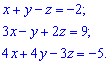
Розв'язок. Перетворимо вихідну систему до східчастого вигляду. Для цього від другого рівняння віднімемо перше. Помножена на 3, а від четвертого віднімемо перше, помножене на 4
. 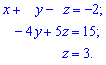
В результаті з третього рівнняня маємо z=3. Отримане значення підставляємо в попереднє рівняння для знаходження y
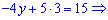 >
>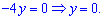
Отримані значення y,z підставляємо в перше рівняння
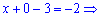
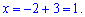
Розв'язком системи трьох лінійних рівнянь будуть наступні значення змінних
x=1; y=0; z=3.
Приклад 2. Знайти розв'язки системи лінійних рівнянь третього порядку.
(4. 195) 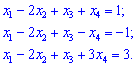
Розв'язок.Задано систему трьох рівнянь з чотирма невідомими. В таких випадках одна змінна може бути вільна, а решта будуть виражатися через неї. Зведемо систему до східчастого вигляду. Для цього від другого і третього рівняння віднімемо перше
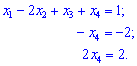
З останніх двох рівнянь отримуємо ідентичні розв'язки x4=1.
Після підстановки в перше рівняння отримаємо
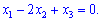
Дане рівняння зв'язує три змінних. Таким чином будь-яка зі змінних може бути виражена через дві інших
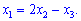
Отже отримаємо наступний розв'язок
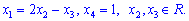
Один з коренів приймає довільне значення, інші виражаюьться через нього.
Приклад 3. Обчисити корені системи лінійних рівнянь 5 порядку.
(4. 198) 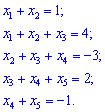
Розв'язок. Ррозріджену систему лінійних рівнянь п'ятого порядку з п'ятьма невідомими зводимо до східчастого вигляду. Від другого рівняння віднімаємо перше і записуємо у зручному для аналізу вигляді (змінні під змінними)
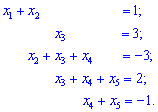
З другого рівняння знаходимо, що x3=3.
Підставляємо значення у всі нижчі рівнняння та переносимо за знак рівності. Також поміняємо друге з третім рівняння місцями
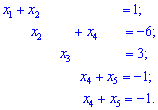
Четверте та п'яте рівняння еквівалентні. Виразимо одну зі змінних через іншу
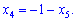
Отримане значення підставимо в друге рівняння і знайдемо x2
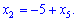
З першого рівняння визначаємо x1
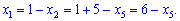
Розв'язок системи рівнянь наступний
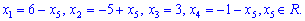
При обчисленнях систем лінійних алгебраїчних рівнянь методом Гауса потрібно звеcти систему лінійних рівннянь до східчастого вигляду. Для цього зручно записувати змінні під змінними, як в останньому прикладі, це пришвидшить розв'язування. Решта все залежить від матриці, яку потрібно розв'язати і Ваших вмінь.
A*X=B
де A - матриця, складена з коефіцієнтів при невідомих; X - стовпець невідомих; B - стовпець вільних членів. Тоді, якщо для матриці A існує обернена матриця A-1 (
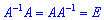 ), то система лінійних рівнянь має єдиний розв'язок і він знаходиться за формулою
), то система лінійних рівнянь має єдиний розв'язок і він знаходиться за формулоюX=A-1*B.
Оскільки перемножити матрицю на вектор стовпець не складає особливих труднощів, то найбільша проблема при обчисленнях – знайти обернену матрицю.
В знаходженні розв'язку за наведеною формулою і полягає суть матричного методу.
Розглянемо декілька прикладів із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Розв'язати систему лінійних алгебраїчних рівнянь.
1) (1. 183) 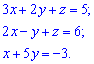
Розв'язок.Запишемо системо трьох лінійних рівнянь у матричній формі
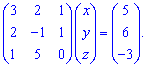
Знайдемо обернену матрицю. Нагадаємо, що її обчислюють за формулою
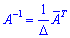
де 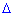 - визначник матриці A , а
- визначник матриці A , а 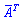 - транспонована матриця алгебраїчних доповнень елементів Aij визначника матриці.
- транспонована матриця алгебраїчних доповнень елементів Aij визначника матриці.
Обчислимо визначник головної матриці
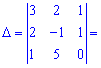
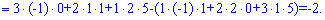
Матрицю алгебраїчних доповнень складається з елементів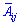 , які обчислюються через мінори за правилом
, які обчислюються через мінори за правилом
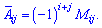
Мінори Mij - це визначники на порядок менші від визначника 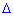 , які утворюються викреслюванням в ньому i -го рядка і j - го стовпця. На перший погляд звучить надто запутано, але при обчисленнях все стане зрозуміло і просто.
, які утворюються викреслюванням в ньому i -го рядка і j - го стовпця. На перший погляд звучить надто запутано, але при обчисленнях все стане зрозуміло і просто.
Знайдемо алгебраїчні доповнення до визначника
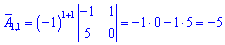
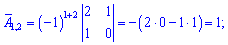
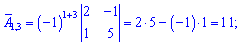
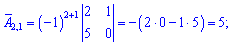
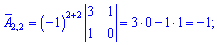
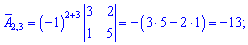
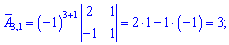
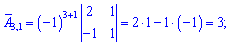
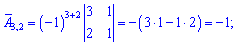
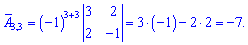
Запишемо знайдену матрицю алгебраїчних доповнень
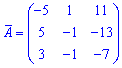
та протранспонуємо її
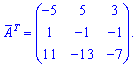
Знаходимо обернену матрицю
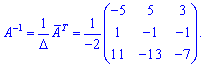
З допомогою оберненої матриці знаходимо розв'язок системи лінійних рівнянь
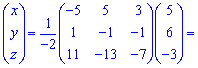
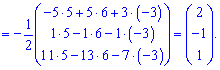
В результаті отримали x1=2;x2=-1; x3=1.
Приклад 2.Знайти розв'язо системи лінійних алгебраїчних рівнянь.
(4. 182) 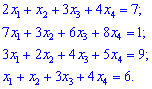
Розв'язок. Cистему лінійних рівнянь четвертого порядку перепишемо в матричній формі
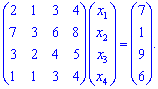
Оскільки всі коефіцієнти ненульві то обчислювати її буде важко. Виконаємо над системою лінійних рівнянь елементарні перетворення, щоб занулити деякі з коефіцієнтів.
Від другого рядка віднімемо перший і останній рядки
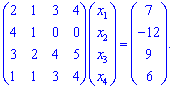
Від третього рядка віднімемо суму першого та четвертого початкової системи
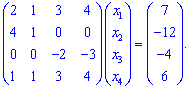
Від четвертого рядка віднімемо перший
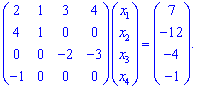
З останнього рядка вже можемо сказати, що перший корінь x1=1 , але будемо дотримуватись правил, щоб навчитися розв'язувати великі системи рівнянь.
Оскільки матриця стала розрідженою, то обчислення визначника та матриці алгебраїчних доповнень спростяться. Знайдемо визначник матриці, розклавши його за четвертим рядком
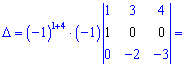
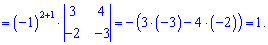
Знайдемо матрицю аглгебраїчних доповнень, розкладаючи шукані детермінанти за рядками і стовпцями, які містять найбільше нулів. Для самоперевірки випишу Вам обчислення тільки першого рядка. Решта спробуйте обчислити самостійно
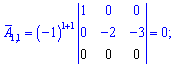
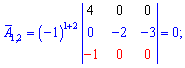
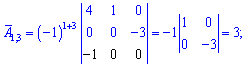
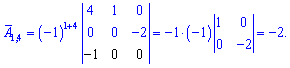
Після знаходження всіх значень отримаємо наступну матрицю доповнень
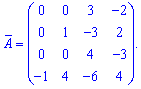
Оскільки визначник рівний одиниці, то обернена матриця з транспонованою матрицею доповнень співпадають
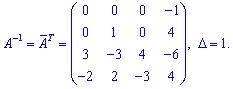
Підставимо у матричний запис та знайдемо розв'язок
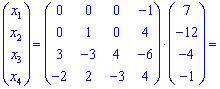
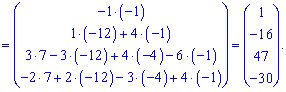
Відповіддю будуть значення x1=1;x2=-16; x3=47; x4=30.
При обчисленнях систем лінійних алгебраїчних рівнянь третього, четвертого порядку матричним методом доводиться знаходити велику кількість алгебраїчних доповнень, які собою являють визначники другого та третього порядку відповідно. Саме помилки при їх обчисленні найчастіше стають причиною невірного розв'язку. Для уникнення таких ситуацій потрібно добре знати правила знаходження визначників другого, третього порядку, а також правила чергування знаків при мінорах.
Вивчайте їх і отримуйте лише вірні розв'язки. Як бонус - можете завантажити калькулятор систем лінійних рівнянь YukhymCalc.