Діаметральна площина поверхні другого порядку

Відрізок, який сполучає дві довільні точки поверхні другого порядку (ПДП), називається хордою цієї поверхні. Множина середин хорд ПДП паралельних до неасимптотичного напряму 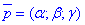 утворює площину, яку називають діаметральною площиною поверхні другого порядку. Таким чином діаметральна площина, це площина що спряжена з напрямом 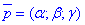, а її рівняння наступне:

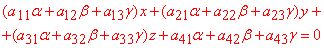
Теорема: Всі діаметральні площини проходять через центр поверхні 2 порядку!

Хто навчається в Львівському національному університеті імені Івана Франка, той може знайти готові відповіді до практикуму з аналітичної геометрії.
Наступні приклади задавали на кафедрі геометрії і топології  механіко-математичного факультету при вивченні вказаних далі тем:

Розділ VI: «Поверхні другого порядку».
Частина IV: «Діаметральні площини »

Приклад 6.4.1 Знайдіть діаметральну площину поверхні 3x²+2y²-z²+3xy-2yz+7=0, яка проходить через точки A(-1;2;0), B(3;0;2).
Розв'язання: Оскільки діаметральна площина проходить через центр ПДП, то спершу знайдемо координати центра. Для цього випишемо коефіцієнти рівняння поверхні другого порядку:
a₁₁=3, a₂₂=2, a₃₃=-1, a₁₂=1.5, a₁₃=0,a₂₃=-1,a₁₄=0, a₂₄=0,a₃₄=0,a₄₄=7.
Хто не знає як, то співставте значення a_ij з рівнянням або перегляньте попередніуроки з поверхонь.
Коефіцієнти потрібні для побудови системи трьох лінійних рівнянь, обчисення якої дає центр поверхні другого порядку:
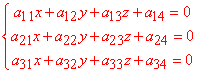Формула є досить простою, а СЛАР в багатьох випадках близька до трикутної форми.
Лише в окремих випадках Вам доведеться застосувати метод Гауса, щоб звести систему рівнянь до східчастого вигляду
Отож складаємо рівняння та обчислюємо
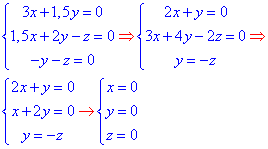Знайшли точку O(0;0;0) - центр поверхні ПДП.
Наступним кроком складаємо рівняння площини, яка проходить через три точки A(-1;2;0), B(3;0;2), O(0;0;0):
для цього застосовуємо формулу визначника
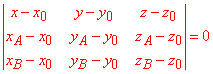Розкладемо визначник через мінори першого рядка
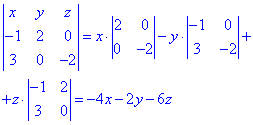Цей метод досить зрозумілий і ефективний, оскільки залишається знайти визначники 2 порядку. В іншому випадку Вам би довелося групувати сталі та коеф. при змінних.
Розділимо праву частину на двійку та прирівняємо до нуля.
Таким чином, ми знайшли рівняння діаметральної площини:
2x+y+3z=0.
Даним алгоритм використовуйте в завданнях, які мають ідентичну умову. Далі будуть розглянуті більш складні в плані обчислень приклади на діаметральні площини.

Приклад 6.4.2 Знайдіть діаметральну площину поверхні 2x²-y²+z²-4x+4z+3=0, яка проходить через точки A(0;-2;1), B(2;-3;0).
Розв'язання: Спершу необхідно визначити координати центру поверхні другого порядку.
Запишемо коефіцієнти рівняння ПДП, які необхідні для складання системи лінійних рівнянь:
a₁₁=2, a₂₂=-12, a₃₃=1, a₁₂=0, a₁₃=0,a₂₃=0,a₁₄=-2, a₂₄=0,a₃₄=2,a₄₄=3.
Складаємо СЛАР та визначаємо

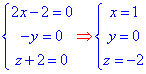
центр поверхні другого порядку (ПДП) -O(1;0;-2).
Побудуємо рівняння площини, яка проходить через три точки A(0;-2;1), B(2;-3;0), O(1;0;-2).
Детермінант запишемо формулою
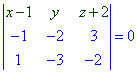Знаходимо визначник через алгебраїчні доповнення до першого рядка
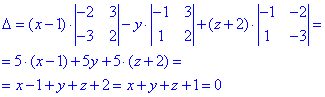Рівняння шуканої діаметральної площини має вигляд:
x+y+z+1=0.
На цьому завдання розв'язано.

Приклад 6.4.3 Знайдіть діаметральну площину поверхні x²-z²+2xy-yz+3y+5=0, яка перпендикулярна до прямої (x+5)/1=(y-1)/2=z/0

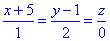
Розв'язання: Записуємо коефіцієнти рівняння заданої поверхні другого порядку:
a₁₁=1, a₂₂=0, a₃₃=-1, a₁₂=1, a₁₃=0,a₂₃=-0.5,a₁₄=0, a₂₄=1.5,a₃₄=0,a₄₄=5.
Повторно наведемо рівняння діаметральної площини, яка паралельна до деякого неасимтотичного напряму 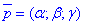в загальному вигляді:

(*)
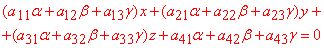
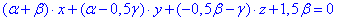Отримали рівняння площини з нормальним вектором:
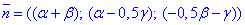Оскільки шукана площина перпендикулярна до заданої прямої (з напрямним вектором 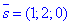), то за властивістю колінеарності 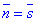прирівнюємо значення координат.
В результаті отримаємо систему трьох рівнянь
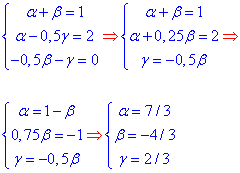з якої знаходимо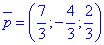
Підставимо координати вектора 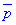у рівняння (*) шуканої площини, отримаємо рівняння діаметральної площини x+2y-2=0.

Приклад 6.4.4 Знайдіть діаметральну площину поверхні y²+z²+2xy+3yz-3y-7=0, яка перпендикулярна до прямої x/(-2)=(y+3)/(-1)=(z-4)/1

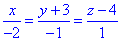
Розв'язання: Уважно виділяємо коефіцієнти рівняння поверхні:
a₁₁=0, a₂₂=1, a₃₃=1, a₁₂=1, a₁₃=0,a₂₃=1.5,a₁₄=0, a₂₄=-1.5,a₃₄=0,a₄₄=-7.
Загальне рівняння діаметральної площини, що паралельна до неасимтотичного напряму 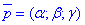задаєься формулою:
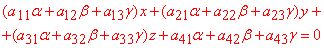При підстановці отримаємо
(**)
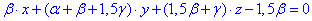Рівняння діаметральної площини матиме нормальний вектор, координати якого є множниами при змінних в тільки що висаному рівнянні:
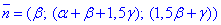Далі за умовою, що шукана площина є перпендикулярною до заданої прямої (з напрямним вектором 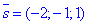, то за властивістю вектори колінеарні: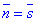
Прирівнюємо їх значення та визначаємо alpha, beta, hamma:
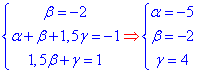Нормальний вектор дыаметральноъ площини має координати .
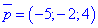Підставимо знайдені значення 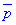у рівняння (**), в резуьтаті отримаємо рівняння діаметральної площини -2x-y+z+3=0, або після множення на (-1) у вигляді
2x+y-z-3=0.

Приклад 6.4.5 Запишіть рівняння тієї діаметральної площини для поверхні
4x²+4y²+12z²-10xy+4yz+4xz-16x-16y+16z-3=0,
яка паралельною до площини x+2y-3z+5=0.
Розв'язання: Коефіцієнти рівняння поверхні рівні:
a₁₁=4, a₂₂=4, a₃₃=12, a₁₂=-5, a₁₃=2,a₂₃=2,a₁₄=-8, a₂₄=-8,a₃₄=8,a₄₄=-3.
Записуємо загальну формулу рівняння діаметральної площини:
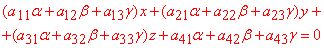та з урахуванням a_ij
(***)
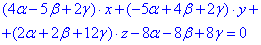Нормальний вектор пощини матиме координати:

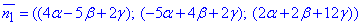
Оскільки невідома діаметральна площина паралельна до заданої в умові площини x+2y-3z+5=0
(з нормальним вектором 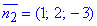), то з умови паралельності маємо: n₁=n₂.
Із системи 3 інійних рівнянь виражаємо alpha, beta, hamma
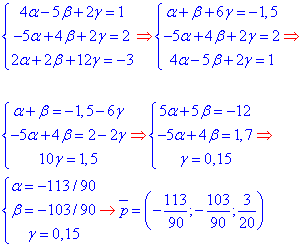та підставяємо у рівняння діаметральної площини (***)
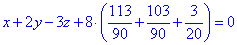або x+2y-3z+20,4=0.
Після трьох проаналізованих завдань думаю Ви готові обчислити такого видуу завдання самостійно.

Приклад 6.4.6 Запишіть рівняння тієї діаметральної площини для поверхні
4x²+4y²+12z²-10xy+4yz+4xz-16x-16y+16z-3=0,
яка є паралельною до площини 2x+y-z+1=0.
Розв'язання: Можливо для когось це буде зайвим проте повторюваність одного і того рано чи пізно приводить до закріплення матеріалу. Тому пройдемося по схемі обчислень на прикладі ще двох рівнянь ПДП.
Першим кроком записуємо коефіцієнти рівняння поверхні:
a₁₁=4, a₂₂=4, a₃₃=12, a₁₂=-5, a₁₃=2,a₂₃=2,a₁₄=-8, a₂₄=-8,a₃₄=8,a₄₄=-3.
Далі за формулою
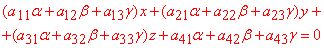складаємо рівняння діаметральної площини в коефіцієнтах нормального вектора
(****)
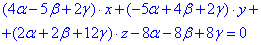Виписуємо координати нормалі:
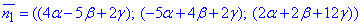та за умовою паралельності до площини 2x+y-z+1=0, що задана початковою умовою, прирівнюємо їх до нормального вектора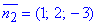
Звідси отримаємо систему трьох лінійних рівнянь
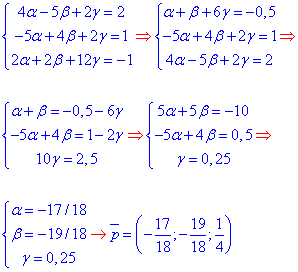обчислення якої і дає alpha, beta, hamma.
Підставимо координати вектора 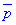у рівняння діаметральної площини
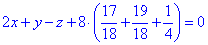після спрощень отримаємо
2x+y-z+18=0.

Задача 6.4.7 Запишіть рівняння тієї діаметральної площини для поверхні
2x²-5y²-3z²-2xy-4xz+2yz-2x-10y-2z-1=0, яка є перпендикулярною до осі ординат.
Розв'язання: Переходимо до розрахунків - спершу a_ij:
a₁₁=2, a₂₂=-5, a₃₃=-3, a₁₂=-1, a₁₃=-2,a₂₃=1,a₁₄=-1, a₂₄=-5,a₃₄=-1,a₄₄=-1.
Рівняння діаметральної площини, яка паралельна до деякого неасимтотичного напряму 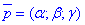після підстановки в формулу:
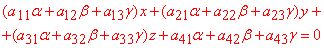спроститься до вигляду
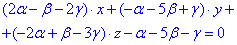Оскільки вісь ординат має напрямний вектор p(0;1;0), то за властивістю паралельності нормальних векторів маємо:
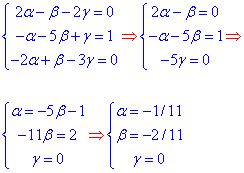Підставляємо координати (alpha; beta; hamma) у рівняння діаметральної площини

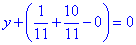
та спрощуємо
y+1=0.

Знання легко не даються, для закріплення матеріалу постійно розв'язуйте по декілька однотипних прикладів на розгянуті умови.
Робіть практичні до тих пір, поки повністю не запам'ятаєте схему розрахунків.
Удачі Вам на практичних та екзаменах!