Поверхні другого порядку https://yukhym.com/uk/poverkhni2.html Thu, 02 May 2024 00:42:41 +0300 Yukhym Comunity - the full lessons for schoolboys and students! uk-ua [email protected] (YukhymComunity) Зведення до канонічного вигляду рівнянь поверхні другого порядку https://yukhym.com/uk/poverkhni2/zvedennia-do-kanonichnoho-vyhliadu-rivnian-poverkhni-2.html https://yukhym.com/uk/poverkhni2/zvedennia-do-kanonichnoho-vyhliadu-rivnian-poverkhni-2.html В попередній статті розглянуті більш прості приклади на типи поверхні другого порядку. В цій та наступних публікаціях наведено аналіз багатьох прикладів, що повністю пояснює можливі алгоритми їх обчислень.

Задача 6.2.2 Визначте тип поверхні другого порядку:
б) x2-3y2+4zx-2yz=0;
Розв'язання: Виконуємо маніпуляції з квадратичними записами, щоб в підсумку отримати повні квадрати
Щоб спростити рівняння поверхні виконуємо заміну змінних:

тоді отримаємо більш компатний запис

Рівняння описує конус.

 Задача в) Визначте тип поверхні другого порядку: 

x2+4y2+z2-4xy-4yz+2xz=0;
Розв'язання: Тут, щоб виділити повні квадрати доведеться вдатия до математичних хитрощів, а все тому, що перед xy маємо знак мінус. Запишемо перетворення
x2+(-2y)2+z2+2x(-2y)+2xz+2(-2y)z=0;
(x-2y+z)2=0.
Без знання формул скороченого множення цей приклад досить довго довелось би розписувати, тому вчіть їх. Чим краще Ви будете ними володіти, тим легше Ви знайдете їм застосування.
Таким чином, отримали дві дійсні площини x-2y+z=0, що збігаються.

Задача г) Звести до канонічного вигляду рівняння поверхні другого порядку: 

x2+5y2+z2+2xy+6xz+2yz-2x+6y-10z=0;
Розв'язання: В цьому завданні не все так легко, як Вам би того хотілося. Метод Лагранжа дасть хороший результат, але до нього ще потрібно дійти.
Тому першим ділом розписуємо рівняння, щоб виділити повні квадрати. Цього разу за добутком змінних потрібно виділити квадрат суми 4 доданків

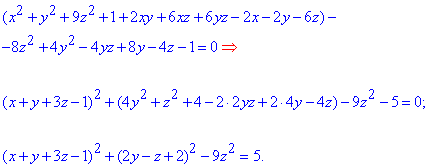
Залишилося зробимо заміну:

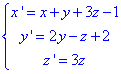
і ми отримаємо

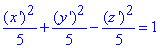
канонічне рівняння однополого гіперболоїда.
Можливо Вам здається , що приклад занадто важкий, проте хто вчиться на факуьтетах з математичним нахилом (математики, прикладники, фізики) на практиці можуть зустріти ще важчі завдання. І повірте, що викладачі, аж ніяк не заінтересовані, щоб Ви швидко навчилися їх рішати.


Задача д) Звести до канонічного вигляду рівняння поверхні другого порядку:
4x2+2y2+10z2-4xy+12xz-8yz=0;
Розв'язання: Як і у попередньому завданні, виділяємо суму квадратів трьох змінних, враховуючи множники при xy, xz, zy. І хоч це завдання не з легких, Ви маєте навчитися їх обчислювати.

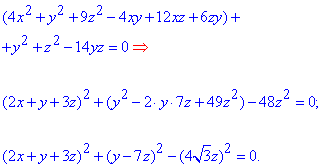
Далі зробимо заміну змінних:

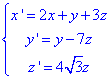
і отримаємо
(x')2+(y')2-(z')2=0.
канонічне рівняння конуса.
Це і є тип поверхні, який потрібно було визначити.

Змінимо дещо умову, а саме знак перед останнім доданком.

 

Задача д) Звести до канонічного вигляду поверхню:
4x2+2y2+10z2-4xy+12xz+8yz=0;
Розв'язання: Це призведе до того, що поміняється невелика частина рівняння поверхні, однак при зведенні до повних квадратів отримаємо не три, а два доданки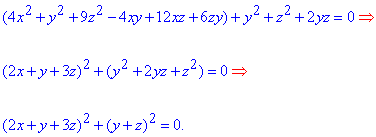

Заміна змінних:

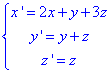
перетворить рівняння поверхні до вигляду
(x')2+(y')2=0.
Повірте, що це не рівняння кола, як багато кому з Вас здається.
Отримали канонічне рівняння двох уявних площин, що перетинаються по дійсній прямій.

 

Задача е) Визначте тип поверхні другого порядку: 

4x2+9y2+z2-12xy+4xz-6yz+4x-6y+2z-5=0;
Розв'язання: Порозписуємо коефіцієнти при змінних в квадраті, щоб бачити в якоу напрямі перетворювати рівняння заданої поверхні

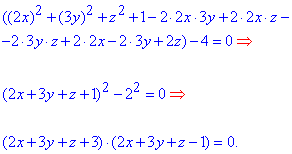
Маніпуляції не всім очевидні, проте правильні. Передостанню формулу розписуємо за різницею квадратів
В підсумку отримали дві дійсні паралельні площини
2x+3y+z+3=0;
2x+3y+z-1=0.
За зворотнім ходом поступають викладачі, придумуючи студентам нові завдання. Беруть два рівняння площин з простими коефіцієнтами при змінних, перемножують їх, і мають нове завдання на поверхні, щоб перевірити як добре Ви знаєте теоретичний матеріал.


Задача є) Звести до канонічного вигляду рівняння поверхні другого порядку:
 x2-2y2+z2+4xy-8xz-4yz-14x-4y+14z+16=0;
Розв'язання: Перегрупуємо доданки, щоб використати формули скороченого множення.

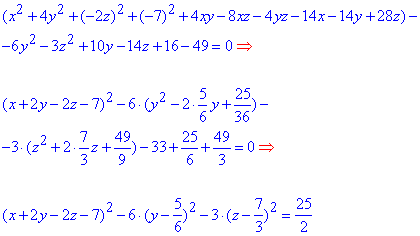
Перехід від першого до другого запису найбільш важчий, тож спробуйте в ньому розібратися самостійно.
Подаьше виділення повних квадратів під силу більшості студентів.
Щоб спростити запис зробимо заміну:

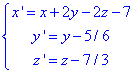
тоді рівняння поверхні 2 порядку спроститься до виду

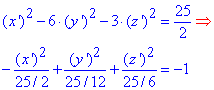
Отримали рівняння двополого гіперболоїда.

 

Задача ж) Визначте тип поверхні другого порядку:
2x2+y2+2z2-2xy-2yz+x-4y-3z+2=0;

Розв'язання: Методика визначення типу поверхні з прикладу в приклад тільки ускладнюється і дане завдання не вийняток.
Щоб не повторюватися наведемо всі формули перетворень, а Ви вже аналізуйте, що і для чого потрібно згруповувати

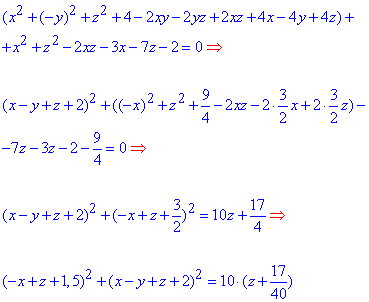
В результаті рівняння поверхні другого порядку стане більш читабельним.
Останній штрих вносить наступна заміна змінних

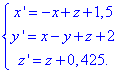
яка дозволяє в формулі
(x')2+(y')2=10z'.
побачити рівняння еліптичного параболоїда.

 

 

Задача з) З'ясуйте тип поверхні другого порядку:
x2+5y2+z2+2xy+6xz+2yz-2x+6y+2z=0.
Розв'язання: Виконуємо маніпуляції, щоб розділити змінні та звести рівняння поверхні другого порядку до канонічного вигляду

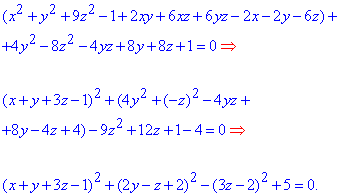
Після виділення повних квадратів залишилося зробимо заміну змінних:
x'=x+y+3z-1;
y'=2y-z+2;
z'=3z-2
і поверхня набуде вигляду
(x')2+(y')2-(z')2=-5.
Рівняння описує двополий гіперболоїд.
На цьому завдання на зведення до канонічного вигляду рівняння поверхні не закінчуються, більше тако сорту прикладів шукайте на сторінках сайту.

]]> [email protected] (Yukhym Roman) Поверхні другого порядку Sun, 02 Oct 2016 18:38:19 +0300 Сфера. Задачі на рівняння сфери https://yukhym.com/uk/poverkhni2/sfera-zadachi-na-rivniannia-sfery.html https://yukhym.com/uk/poverkhni2/sfera-zadachi-na-rivniannia-sfery.html Сфера – множина (геометричне місце) точок простору, рівновіддалених від фіксованої точки. Ця фіксована точка O(x0; y0; z0) називається центром сфери, а відстань від довільної точки сфери до її центра називається радіусом сфери R.
Канонічне рівняння сфери:
x2+y2+z2=R2, де R - радіус сфери.

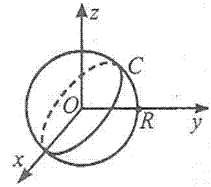
Формула сфери з центром у точці O(x0; y0; z0) і радіусом R:
(x-x0)2+(y-y0)2+(z-z0)2=R2

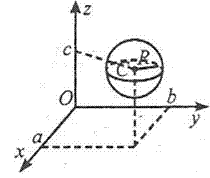
Будь-яка дотична пряма або площина перпендикулярна до радіуса сфери в точці дотику.

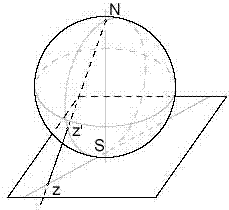
Основні формули сфери

  1. Площа сфери
    площа сфери
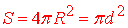
  2. Об'єм кулі, обмеженої сферою
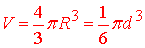
    Об'єм кулі
  3. Площа сегменту сфери

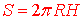
    Сегмент сфери- смуга між екватором і широтою, проведеною на висоті H над екватором.

Чимало задач на площу поверхні сфери і об'єм кулі Ви розглянули в шкільному курсі, проте це не складні задачі. Тут же будуть проаналізовані приклади, які Вас чекають при навчанні у ВУЗах. Уважно вивчайте їх та використовуйте на практиці.

Задачі на складання рівнянь сфери

Задача 6.1.1 Запишіть рівняння сфери, яка:

  1. має центр в точці (2;-1;3) і радіус R=6;
  2. має центр в початку координат (0;0;0) і проходить через точку (6;-2;3);
  3. має центр в точці (1;4;-7) і дотикається до площини 6x+6y-7z+42=0;
  4. має центр в точці (6;-8;3) і дотикається до осі аплікат.

Розв'язання: Наведена схема обчислень універсальна і застосовується в ряді подібних завдань.
1) Маємо координати центра O(x0;y0;z0) і радіус сфери R.
Складемо рівняння сфери з центром у точці (2;-1;3) і радіусом R=6:
(x-2)2+(y+1)2+(z-3)2=36.
Це найбільш простий приклад з яким може справитися і школяр.

2) Задано координати центра сфери O(x0;y0;z0) і координати точки, що належить сфері M(xM;yM;zM).
Запишемо формулу для знаходження радіуса сфери – відстань між центром сфери O(0;0;0) і точкою, що належить сфері M(6;2;-3):

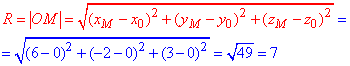
Так як центр знаходиться в початку координат то отримаємо канонічне рівняння сфери з радіусом R=7:
x2+y2+z2=49.

3) Відомі координати центра сфери O(x0;y0;z0) і рівняння дотичної площини a*x+b*y+c*z+d=0.
Знайдемо радіус сфери через відстань від центра сфери (1;4;-7) до точки дотику з площиною 6x+6y-7z+42=0 з нормальним вектором (6;6;-7) (значення беремо з р-ня площини):

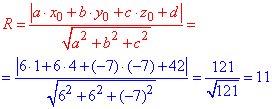
Формула не складна і після обчислень радіус рівний R=7.
Складаємо рівняння сфери з центром у заданій точці (1;4;-7) і R=11:
(x-1)2+(y-4)2+(z+7)2=121.
Запам'ятайте або випишіть наведену формулу, в плані розрахунків вона не складна.

4) Нехай маємо координати центра сфери O(x0;y0;z0) і дотичну до сфери вісь Oz.
Знайдемо радіус сфери як відстань від центра сфери (6;-8;3) до точки дотику K(0;0;3) з віссю аплікат - Oz за формулою


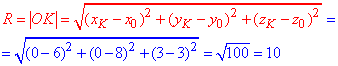
За відомим центром у точці (6;-8;3 і радіусом R=10 записуємо рівняння сфери:
(x-6)2+(y+8)2+(z-3)2=100.

 

Задача 6.1.2 Складіть рівняння описаної навколо трикутної піраміди ABCD сфери, якщо відомо координати вершин піраміди A(2;0;0), B(0;5;0), C(0;0;3),D(0;0;0).
Розв'язання: Оскільки трикутна піраміда ABCD вписана у сферу, то її вершини належать сфері. Тому відстань від центра сфери O(x0;y0;z0) до вершин піраміди однакова і є радіусом сфери R. Запишемо відстань від центру до точки A(2;0;0):
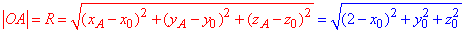відстань між точками.
Запишемо відстань від точки O(x0;y0;z0) до точки B(0;5;0):
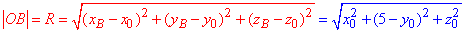Запишемо відстань від точки O(x0;y0;z0) до точки C(0;0;3):

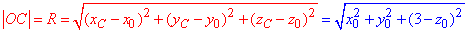
Запишемо відстань від точки O(x0;y0;z0) до точки D(0;0;0):

відстань між точками
Прирівняємо відстань |OD|2 з кожною іншою, таким чином складемо систему трьох рівнянь з трьома невідомими:
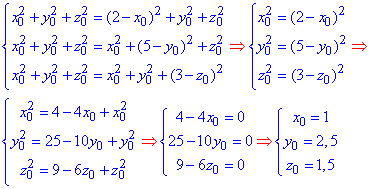
система рівнянь
звідси остаточно отримаємо координати центра сфери O(x0;y0;z0)=(1;2,5;1,5).
Обчислимо радіус сфери за формулою:

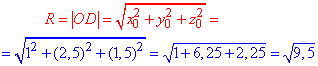
За наведеними на початку статті формулами складаємо рівняння сфери з центром у точці О(1;2,5;1,5) і радіусом :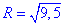
(x-1)2+(y-2,5)2+(z-1,5)2=9,5

 

Задача 6.1.3 Визначте центр та радіус сфери:
а) x2+y2+z2-6x+8y+2z+10=0.
Розв'язання: Тут необхідно звести рівняння сфери до канонічного вигляду (методом виділення повних квадратів):
Перше рівняння при виділенні квадратів перетвориться наступним чином
x2-6x+9+y2+8y+16+z2+2z+1-9-16-1+10=0,
(x-3)2+(y+4)2+(z+1)2-16=0,
(x-3)2+(y+4)2+(z+1)2=42.
Отримали сферу з центром у точці O(3;-4;-1) та радіусом R=4.

б) x2+y2+z2+2x-4y-4=0;
Розв'язання: Доповнюємо квадратичні вирази до повних квадратів, а щоб компенсувати це від вільного члена віднімаємо квадрати сталих
x2+2x+1+y2-4y+4+z2-1-4-4=0,
(x+1)2+(y-2)2+z2-9=0,
(x+1)2+(y-2)2+z2=32.
Кінцеве рівняння описує сферу з центром O(-1;2;0) і радіусом R=3.

в) x2+y2+z2-6x+10=0;
Розв'язання:Виділимо повні квадрати у залежності
x2-6x+9+y2+z2-9+10=0,
(x-3)2+y2+z2+1=0,
(x-3)2+y2+z2=-1.
Отримали, сферу у якої квадрат радіуса від'ємний, а це значить, що маємо справу з комплексними числами.
i2=-1, R=i.
Отримали уявну сферу з центром в O(-1;2;0) і радіусом .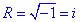

г) x2+y2+z2-4x+12y-2z+41=0;
Розв'язання: Виділяємо повні квадрати і зводимо рівняння до канонічного вигляду
x2-4x+4+y2+12y+36+z2-2z+1-4-36-1+41=0,
(x-2)2+(y+6)2+(z-1)2=0.
Маємо окремий випадок «сфери» з центром O(2;-6;1) і радіусом R=0, що означає сфера вироджена в точку.

д) 36x2+36y2+36z2-36x+24y-72z-95=0.
Розв'язання: Тут слід бути уважними оскільки перед змінними маємо множники відмінні від одиниці. При зведенні до повних квадратів отримаємо
36x2+36y2+36z2-36x+24y-72z-95=0
36(x2-x+1/4)-36/4+36(y2+2/3*y+1/9)-36/9+36(z2-2z+1)-36-95=0,
36(x-1/2)2+36(y+1/3)2+(z-1)2-9-4-36-95=0,
36(x-1/2)2+36(y+1/3)2+(z-1)2-144=0,
(x-1/2)2+(y+1/3)2+(z-1)2=144/36=4.
Не забувайте вкінці обчислень нормувати рівняння на множник при "дужках". Задане рівняння описує сферу з центром 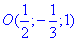і радіусом R=2.
Будьте уважні в подібних завданнях!


Задача 6.1.4 Запишіть рівняння сфери, що проходить через три точки (3;1;-3), (-2;4;1), (-5;0;0) і її центр лежить на площині 2x+y-z+3.
Розв'язання: Завдання не з простих, тому спробуйте вивчити алгоритм розрахунків.
З курсу математики відомо, що відстань від центра сфери O(x0;y0;z0) до кожної заданої точки є постійною і рівна радіусу сфери R.
Запишемо радіус в кожному із випадків за формулою відстані між двома точками.
Таким чином від центра O(x0;y0;z0) до першої точки A(3;1;-3) матимемо:

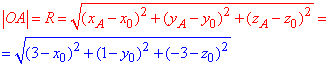
Далі розписуємо формулу відстані від точки O(x0;y0;z0)до точки B(-2;4;1):

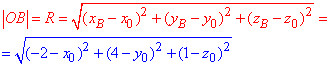
І наостанок віддаль до точки C(-5;0;0):

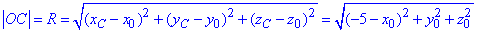
Подальші роздуми приводять до висновків:
оскільки центр сфери O(x0;y0;z0) належить заданій площині, тому можемо записати її рівняння у вигляді
2x0+y0-z0+3=0,
звідки виражаємо одну зі змінних z0=2x0+y0+3 (*).
Прирівняємо відстань |OC|2 з кожною іншою + врахуємо рівняння площини(*), таким чином дістанемо систему трьох рівнянь з трьома невідомими. Нижче наведені обчислення системи трьох рівнянь, яка при розписанні спрощується до лінійних
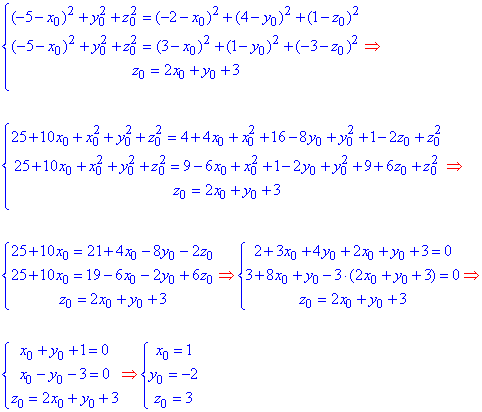
система рівнянь
Знайдені координати центра сфери O(1;-2;3) підставляємо в будь-яке із рівнянь відстані та .
обчислюємо радіус сфери:

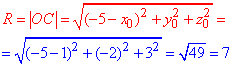
Він рівний R=7, звідси R2=49.
Скласти рівняння сфери при відомому центрі O(1;-2;3) і радіусі досить просто:
(x-1)2+(y+2)2+(z-3)2=49.
Перегляньте уважно відповідь та запам'ятайте хід обчислень.


Задача 6.1.5 Запишіть рівняння сфери, що проходить через чотири точки (1;-2;-1), (-5;10;-1), (4;1;11), (-8;-2;2).
Розв'язання: Як Вам відомо, відстань від центра сфери до кожної точки на поверхні є сталою, яка характеризує радіус сфери.
Як і в попередньому завданні, складаємо рівняння відстані від центру до заданих точок. Для першої A(1;-2;-1) отримаємо:

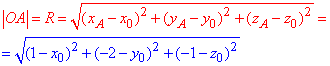
Для другої точки B(-5;10;-1) наступне значення:

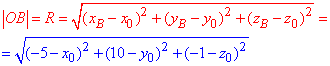
Точка C(4;1;11) від центру віддалена на |OC|:

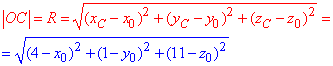
Відстань від четвертої точки D(-8;-2;2) до центру сфери рівна:

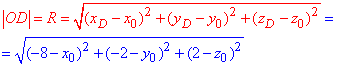
На відміну від попереднього прикладу немаємо площини, проте її компенсовує ще одна точка на сфері.
Для простоти обчислень прирівняємо квадрат відстані |OA|2 з кожною іншою і складемо систему трьох рівнянь для визначення трьох невідомих. Усі перетворення, які при цьому виконуємо можна записати формулами
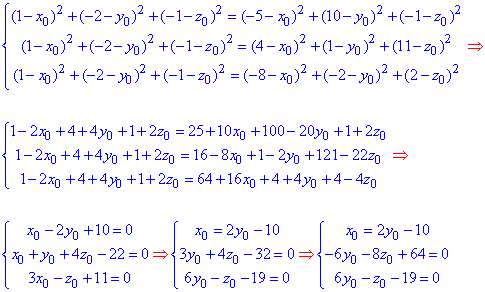
система рівнянь, центр сфери
З останньої системи рівнянь отримали наступні координати центру сфери O(-2;4;5).
Підставляємо в одне з рівнянь та обчислюємо радіус сфери:

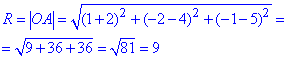
Він рівний R=9.
Маємо все необхідне для складання рівняння сфери:
(x+2)2+(y-4)2+(z-5)2=81.

Задача 6.1.6 Запишіть рівняння сфери радіуса R, яка дотикається:
а) до трьох координатних площин;
б) до трьох координатних осей.
Розв'язання:
а) Прямокутна декартова система координат має вісім октантів. Якщо в кожен із них помістити сферу, яка буде перпендикулярна до трьох площин, то координати центра сфери запишуться 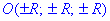, то рівняння сфери матиме вигляд.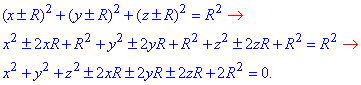
Слід відмітити, що знак «мінус» буде стояти залежно від того, в якому октанті розміщається сфера.
Він може бути присутній при будь-якому множнику, подумайте чому так?

б) Рівняння сфери, яка дотикається до осей в першому октанті матиме вигляд
(x-a)2+(y-a)2+(z-a)2=R2.
При цьому, якщо точка належить осі, то її координати рівні, наприклад (a;0;0).
При підстановці в попереднє рівняння отримаємо
(a-a)2+(0-a)2+(0-a)2=R2,
2a2=R2,
a2=R2/2.
Добувши корінь квадратний отримаємо, що координати центра сфери для різних октантів можна записати формулою

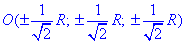
Підставимо центр O в рівняння сфери та розпишемо
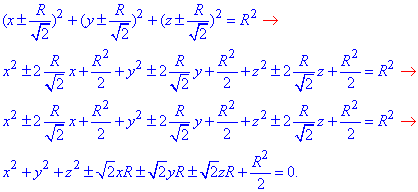
рівняння сфери
Тут також знак "мінус" входить у відповідності до того, в якому октанті розглядаємо сферу.


Задача 6.1.7 З'ясуйте, як розташована точка A(2;-1;3) стосовно кожної зі сфер:
а) (x-3)2+(y+1)2+(z-1)2=4;
Розв'язання: Для обчислення прикладів Ви повинні знати наступні правила:

  1. Якщо (xA-x0)2+(yA-y0)2+(zA-z0)2>R2, то точка знаходиться ззовні сфери.
  2. Коли виконується умова (xA-x0)2+(yA-y0)2+(zA-z0)2=R2, то точка знаходиться на (поверхні) сфери.
  3. При (xA-x0)2+(yA-y0)2+(zA-z0)2<R2 точка знаходиться всередині сфери.

Підставляємо координати точки в перше із заданих рівнянь
(2-3)2+(-1+1)2+(3-1)2=1+0+4=5>4=R2.
Маємо першу умову, тому робимо висновок, що точка A(2;-1;3) знаходиться ззовні заданої сфери;

б) (x+14)2+(y-11)2+(z+12)2=625;
Розв'язання:Обчислюємо відстань
(2+14)2+(-1-11)2+(3+12)2=256+144+225=625=R2.
Отримали, що точка A(2;-1;3) знаходиться на поверхні сфери.


в) (x-6)2+(y-1)2+(z-2)2=25.
Розв'язання:Підставляємо точку у рівняння
(2-6)2+(-1-1)2+(3-2)2=16+4+1=21<625=R2.
За третьою ознакою точка A(2;-1;3) знаходиться всередині сфери.


Задача 6.1.8 Обчисліть найкоротшу відстань від точки A до заданої сфери:
а) A(-2;6;-3),x2+y2+z2=4.
Розв'язання: Завдання не настільки важке, як виглядає на перший погляд.
Вам лише потрібно знати, що найкоротша відстань d від точки A(xA;yA;zA) до сфери з центром O(x0; y0; z0) і радіусом R рівна різниці між відстанню від точки до центра сфери |OA| і радіусом сфери R:
d=|OA|-R.
Рівняння сфери x2+y2+z2=4 має канонічний вигляд, центр якої в початку координат O(0; 0; 0) і радіусом R=2.
Спершу знаходимо відстань від точки A(-2;6;-3) до точки O(0; 0; 0) :

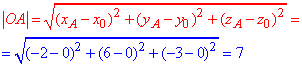
Найкоротшу відстань від точки A(-2;6;-3) до заданої сфери обчислюємо згідно формули:
d=|OA|-R=7-2=5.
Ось така легка схема обчислення задач.

б) A(9;-4;-3), x2+y2+z2+14x-16y-24z+241=0.
Розв'язання: Спершу необхідно в рівнянні сфери виділити повні квадрати, щоб знати реальне положення центру та сам радіус.
x2+14x+49+y2-16y+64+z2-24z+144-49-64-144+241=0,
(x+7)2+(y-8)2+(z-12)2=42.
Такий запис легко читати - сфера з центром O(-7;8;12) і радіусом R=4.
Відстань від точки A(9;-4;-3) до центра сфери O(-7;8;12) рівна:

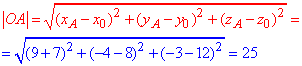
Знаходимо найкоротшу відстань від точки A до сфери:
d=|OA|-R=25-4=21.


в) A(1;-1;3), x2+y2+z2-6x+4y-10z-62=0.
Розв'язання: Виражаємо повні квадрати у рівнянні
x2-6x+9+y2+4y+4+z2-10z+25-9-4-25-62=0,
(x+3)2+(y+2)2+(z-5)2=102.
Сфера з центром в O(3;-2;5) і радіусом R=10.
Обчислюємо відстань від точки A до центра сфери:

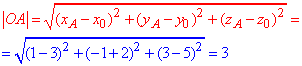
Тоді найкоротша відстань від точки A(1;-1;3) до сфери визначається з формули:
d=||OA|-R|=|3-10|=|-7|=7.
Знак "мінус" означає, що точка A знаходиться всередині заданої сфери, це не важко уявити.


Задача 6.1.9 Визначте, як розташована пряма стосовно сфери:
а)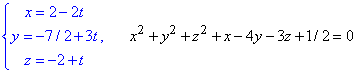
Розв'язання: Щоб визначити розташування прямої (в просторі) відносно сфери, необхідно підставити параметричні рівняння прямої в рівняння сфери і обчислити дискримінант D квадратного рівняння: Далі можливі три варіанти:

  1. Якщо D2>0, то квадратне рівняння має два різних (дійсних) корені, тому пряма проходить через сферу у двох різних точках.
  2. Якщо D2=0, то квадратне рівняння має один корінь, тому пряма перетинає сферу у двох дійсних точках, що збігаються і є дотичною до цієї сфери.
  3. Якщо D2<0, то квадратне рівняння не має (дійсних) коренів, тому пряма

Покажемо, як виглядає аналіз прикладів на практиці.
x=2-2t, y=-7/2+3t, z=-2+t - рівняння прямої (в просторі) заданої параметрично.
x2+y2+z2+x+4y-3z+ 1/2=0 - задана сфера.
Підставимо параметризований запис прямої в рівняння заданої сфери та зводимо останнє до вигляду квадратного рівняння:
(2-2t)2+(-3,5+3t)2+(-2+t)2+2-2t+4(-3,5+3t)-3(-2+t)+ 1/2=0;
4-8t+4t^2+12,25-21+9t^2+4-4t+t^2+2-2t+14-12t+6-3t+0,5;
14t^2-50t+42,75=0.
Знаходимо дискримінант рівняння
D^2=50^2-4*14*42,75=2500-2394=106>0.
За першою ознакою пряма перетинає сферу у двох дійсних точках.

Задача 6.1.9 З'ясувати як розміщена пряма стосовно сфери:

б)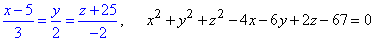
Розв'язання: Перше з двох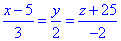 - канонічне рівняння прямої (в просторі), його ще потрібно перетворити до параметричного виду.
Друге рівняння x2+y2+z2+x+4y-3z+ 1/2=0 - задає сферу.
Приведемо рівняння прямої до параметричного вигляду:

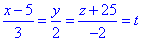
тобто x-5=3t, y=2t, z+25=-2t,
отримали x=5+3t, y=2t, z=-25-2t - параметричне рівняння прямої (в просторі).
Підставимо рівняння прямої в формулу для сфери:
(5+3t)2+(2t)2+(-25-2t)2-4(5+3t)-6*2t+2(-25-2t)-67=0;
25+30t+9t2+4t2+625+100t-+4t2-20-12t-12t-50-4t-67=0;
17t2+102t+513=0.
Обчислюємо квадрат дискримінанту квадратного рівняння
D2=1022-4*17*513=10404-34884=-24480<0.
За третьою ознакою пряма не перетинає задану сферу, а проходить повз неї.


Задача 6.1.9 Визначте як розміщена пряма по відношенню до сфери:

в)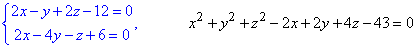
Розв'язання: Перше рівняння описує пряму через перетин двох площин. Друге описує сферичну поверхню.
Перш за все нам необхідно рівняння прямої (в просторі) перевести в параметричну форму запису.
Для цього знайдемо напрямний вектор площини і точку, що належить прямій.
Напрямний вектор прямої в просторі 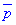– це векторний добуток 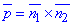двох нормальних векторів площин 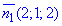і 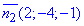, що утворюють пряму при перетині. Їх значення виписуємо як відповідні множники при "x,y,z".
Векторний добуток знаходимо за формулою

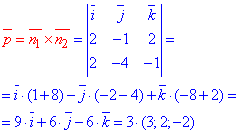
Знайдемо точку, що належить прямій (в просторі), для цього виберемо одну з координат (нехай x=0) та підставимо у систему рівнянь:

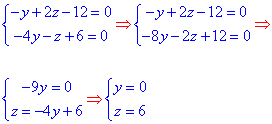
Отож точка M(0;0;6) належить прямій. Тому з врахуванням векторного добутку матимемо

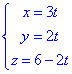
- рівняння прямої (в просторі) заданої параметрично.
Далі, за відомою з попереднього пункту схемою, підставимо параметризовані координати прямої в рівняння сфери:
(3t)^2+(2t)^2+(6-2t)^2-2*3t+2*2t+4(6-2t)-43=0;
17t2-34t +17=0 або t2-2t+1=0.
Дискримінант квадратного рівняння
D2=22-4*1*1=4-4=0.
Отож, пряма перетинає задану сферу у 2 дійсних точках, що збігаються, тобто є дотичною до сфери.

 

Задача 6.1.10 Запишіть рівняння площин, які проходять через пряму 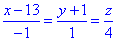і дотикаються до сфери
x2+y2+z2-2x-4y-6z-67=0.
Розв'язання: Запишемо рівняння площини з нормальним вектором 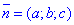і точкою M0(x0; y0; z0):
a(x-x0)+ b(y-y0)+c(z- z0)=0.
Оскільки пряма з точкою M0(-13; -1;0) належить площині, то рівняння площини набуде вигляду:
a(x-13)+ b(y+1)+c(z- z0)=0. (*).
Запишемо рівняння заданої сфери в канонічному вигляді:
x2-2x+1+y2-4y+4+z2-6z+9-1-4-9-67=0;
(x-1)2+(y-2)2+(z-3)2=92 - рівняння сфери з центром O(1; 2;3) і радіусом R=9.
Запишемо рівняння прямої (в просторі) з напрямним вектором 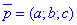, що проходить через центр сфери O (ця пряма буде перпендикулярна до шуканої площини, а її напрямний вектор 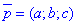- перпендикулярний до напрямного вектора заданої прямої ):

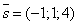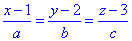
Умова перпендикулярності прямих:
-1*a+1*b+4*c=0;
a-b-4c=0. (1)
Знайдемо відстань від точки O(1; 2;3) до площини a(x-13)+ b(y+1)+c(z- z0)=0:

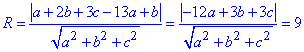
Перенісши корінь із знаменника в праву частину та спростивши на трійку, отримаємо

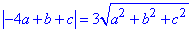
(-4a+b+c)2=9(a2+b2+c2).
Довизначимо одну з сталих, нехай 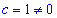, тоді
(-4a+b+1)2=9(a2+b2+c2);
16a^2+b^2-8ab-8a+2b+1=9a^2+9b^2+9;
7a^2-8b^2-8ab-8a+2b-8=0 (2).
Запишемо систему двох рівнянь (1) і (2) (при c=1):

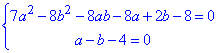
звідси

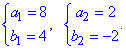
Отримали нормальні вектори прямих 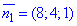і .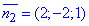
Зазначимо, що ми прийняли координату с=1, оскільки для довільної відмінної від нуля сталої 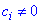вектори 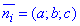будуть компланарні, а при с=0 маємо нульовий вектор a=b=0 (це випливає із системи рівнянь (1) і (2)), чого не може бути.
Підставимо ці вектори у співвідношення (*).
Рівняння шуканих площин запишемо формулами:
8(x-13)+4(y+1)+z=0 або 8x+4y+z-100=0;
2(x-13)-2(y+1)+z=0 або 2x-2y+z-28=0.

 

Задача 6.1.11 Знайдіть рівняння сфери, яка проходить через початок координат і через коло

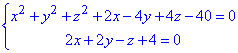
Розв'язання: Щоб записати рівняння сфери необхідно мати:

  • координати центра і радіус сфери;
  • координати центра сфери і точки, що належить сфері;
  • чотири точки, що належать сфері.

З умови задачі маємо першу точку, що належить сфері A(0;0;0).
Із заданого рівняння кола (перетин сфери і площини), яке належить шуканій сфері, знайдемо ще три точки, що належить колу, а, отже, і шуканій сфері. Для z=0 маємо

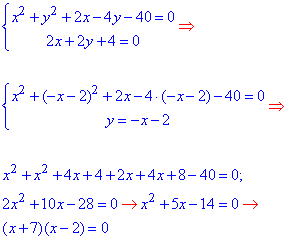
Отримали дві точки B(7;-9;0) і С(2;-4;0).
Для z=4 маємо

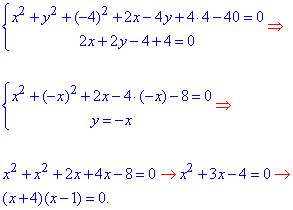
Отож отримали ще дві точки D(1;-1;4), E(-4;4;4).
Через чотири точки A,C,D,E запишемо рівняння шуканої сфери.
Для цього знайдемо координати центра і радіус сфери. Запишемо відстань від точки O до точки A:

Далі знайдемо відстань від точки O до точки C:
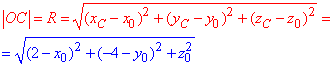Від початку координат до точки D(1;-1;4) відстань рівна:

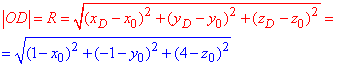
Останнє значення відстані між точками O до точки E(-4;4;4) знаходимо за правилом:

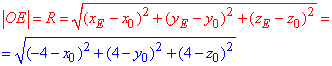
Прирівняємо відстань |OA|2 з кожною іншою, таким чином утворимо систему трьох лінійних рівнянь з трьома невідомими:

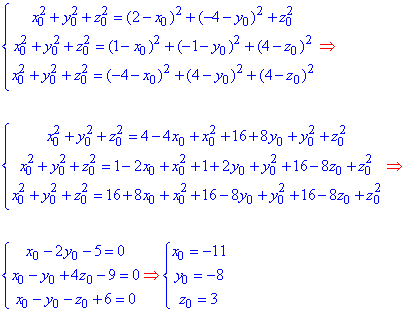
звідси x0=-11, y0=-8; z0=3. Обчислюємо радіус сфери:

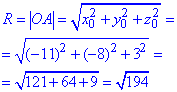
та підставляємо всі знайдені значення в формулу сфери
(x+11)2+(y+8)2+(z-3)2=194 або x2+y2+z2+22x+16y-6z=0.
На цьому пояснення до завдання завершені і переходимо до розгляду наступного прикладу.


Задача 6.1.12 Знайдіть рівняння сфери, яка проходить через коло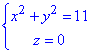 і дотикається до площини x+y+z-5=0.
Розв'язання: Коло, яке належить шуканій сфері є перетином циліндра з віссю Oz і площиною z=0, тобто перпендикулярною до осі Oz. Тому центр кола лежить на одній прямій (осі Oz) з центром шуканої сфери. Координати центра кола S(0;0), тому координати центра шуканої сфери є O(0;0;z0).
Візьмемо точку на колі 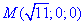, яка одночасно належить сфері, тоді
R2=(xM-x0)2+(yM-y0)2+(zM-z0)2,
тобто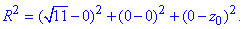
Спростивши, матимемо
R2=11+z02 (1).
Відстань від точки (центра кола) O(0;0;z0) до площини x+y+z-5=0 є радіусом сфери R, оскільки задана площина є дотичною до сфери. Це дає підстави скласти другу залежність для радіуса

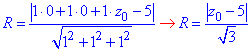
звідси R2=(z0-5)2/3 (2).
Прирівняємо вирази (1) і (2) та знайдемо координати центра і радіус сфери:

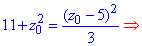
33+z02=z02-10z0+25;
2z02+10z0+8=0;
z0=-1 i z0=-4.
У відповідності до розрахунків отримаємо два кола з радіусами:

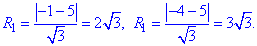
Записуємо рівняння сфери:
x2+y2+(z+1)2=12 і x2+y2+(z+4)2=27.
Подібних прикладів на сферу можна навести тисячі, всі вони та чи інакше пов'язані, а схеми обчислень подібні.
Вчіть формули та з користю застосовуйте на практиці!

]]> [email protected] (Yukhym Roman) Поверхні другого порядку Sun, 25 Sep 2016 08:44:04 +0300 Поверхні другого порядку. Практикум https://yukhym.com/uk/poverkhni2/poverkhni-druhoho-poriadku-praktykum.html https://yukhym.com/uk/poverkhni2/poverkhni-druhoho-poriadku-praktykum.html Дослідження поверхонь другого порядку пов'язано з обчисленням систем лінійних рівнянь, диференціюванням, заміною змінних, і без знання всього цього Ви не завжди зможете знайти правильну відповідь.
Наведені нижче приклади задавали в ЛНУ ім. І. Франка, механіко-математичний факультет, кафедра геометрії і топології

ПРАКТИКУМ з аналітичної геометрії

Розділ VI: «Поверхні другого порядку».
Частина IІ: «Загальна теорія поверхонь другого порядку».
Частина IІІ: «Центр поверхні другого порядку».

Поверхнею другого порядку (ПДП) називається множина точок простору, координати яких в деякій афінній системі координат задовольняють рівняння другого порядку
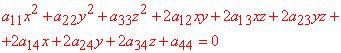рівняння поверхні 2 порядку (1)
причому хоча б один з коефіцієнтів при подвійних добутках змінних відмінний від нуля

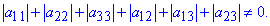
Приймаємо, що aij=aji, тобто матриця складена з коефіцієнтів рівняння симетрична. Точка S називається центром поверхні другого порядку, якщо разом з довільною точкою М цієї поверхні їй належить і точка M', симетрична до точки M стосовно точки S.
Точка S є центром поверхні (2) тоді і лише тоді, коли її координати задовольняють систему рівнянь:
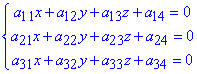
центр поверхні
(або в 1, 2 і 3 рівнянні необхідно взяти частинну похідну по змінній x, y, z відповідно).

Задачі на поверхні другого порядку

Задача 6.2.1 Визначте тип поверхні другого порядку:
а) x2+y2+z2-12x+4y-6z+24=0.
Розв'язання: Схема обчислень одна і та ж для всіх завдань з такою умовою, тому уважно прослідкуйте за наступними перетвореннями.
Зведемо рівняння поверхні другого порядку до канонічного вигляду методом виділення повних квадратів:
x2-12x+36+y2+4y+4+z2-6z+9-36-4-9+24=0.
Як доповнювати квадратичну форму до повного порядку Ви повинні знати, якщо ні уважно слідкуйте як ми перетворюємо формули і за кілька занять опануєте методику. В результаті прийдемо до рівняння
(x-6)2+(y+2)2+(z-3)2=52.
Тут опущені сумування вільного члена, проте в правильності можете переконатися самостійно.
Отримали рівняння сфери з центром O(6;-2;3) і радіусом R=5.


Задача 6.2.2 Визначте тип поверхні другого порядку:
а) 4x2-2y2-12z2+4xy+12yz=0;
Розв'язання: Ви повинні знати, що на практиці Вам не зададуть завдань, які важко вирішити. Тож в більшості випадків поверхню другого порядку потрібно зводити до канонічного вигляду методом виділення повних квадратів. Підказкою служать коефіцієнти, наприклад маємо
4x2+4xy.
До повного квадрату (2x+y)2 тут не вистачає y2.
Отож додаємо та віднімаємо y2, щоб отримати повний квадрат і, одночасно, не змінити рівняння поверхні.
І так само аналізуємо решту частини рівняння.
В результаті отримаємо наступні перетворення
4x2+4xy+y2-3y2+12yz-12z2=0;
(2x+y)2-3(y-2z)2=0.
Оскільки права частина рівняння рівна нулю, то маємо формулу різниці квадратів, яку можемо записати через добуток

Отримали дві дійсні площини
площини
що перетинаються по дійсній прямій.
Це і є шуканим типом поверхні.
Пояснення, думаю, зрозумілі всім, тому переходимо до інших завдань, тим більше що їх тут ще багато.


Задача 6.3.1 Знайдіть центр поверхні другого порядку:
а) 2x2-y2+z2-4x+4z+3=0.
Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку:
a11=2, a22=-1, a33=1, a12=0, a13=0,a23=0,a14=-2, a24=0,a34=2,a44=3.
Знайдемо центр поверхні другого порядку (ПДП), для цього складаємо систему з трьох лінійних рівнянь та обчислюємо її:
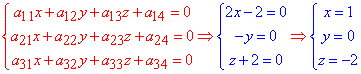
центр поверхні
Точка з координатами O(1;0;-2) є центром заданої поверхні другого порядку.
З розрахунків Ви бачите, що основною задачею тут є правильно та швидко розв'язати систему лінійних рівнянь. Щоб її отримати потрібно без помилок виписати коефіцієнти при квадратичній формі запису поверхні, що теж не є важко. Всі необхідні формули Вам відомі, тож ваші результати на практиці залежать лише від знань цих формул.

Задача 6.3.2 Перенесіть початок координат в центр поверхні другого порядку:
а) x2+2y2+2z2+2xy-2x-4y-4z=0;
Розв'язання: Завдання дещо складніше від попередніх, оскільки щоб перенести початок координат в центр поверхні спершу необхідно цей центр знайти. Крім цього потрібно зробити заміну координат, що автоматом потягне за собою перетворення поверхні. Тут є багато місць де можна допустити помилку, тож уважно обчислюйте та не спішіть. Уважно розгляньте універсальний алгоритм для такого виду завдань.
Зведемо спершу рівняння поверхні другого порядку до канонічного вигляду: 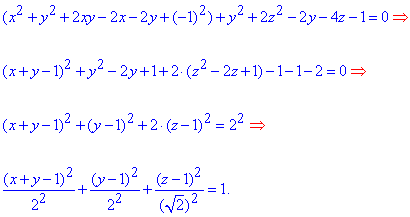канонічна поверхня
Тут всі маніпуляції з рівнянням поверхні повинні бути Вам зрозумілі.
Далі необхідно виконати заміну змінних

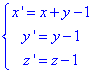
тоді отримаємо

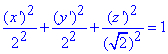
канонічне рівняння еліпсоїда обертання.
Наступним кроком необхідно визначити центр поверхні, для цього із перетвореного рівняння еліпсоїда виписуємо коефіцієнти:
a11=1, a22=2, a33=2, a12=1, a13=0, a23=0, a14=-1, a24=-2, a34=-2, a44=0.
З них складаємо СЛАР для знаходження центру еліпсоїда:
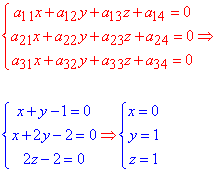
центр поверхні
Точка O(0;1;1) - центр еліпсоїда.
Далі потрібно перенести початок координат в центр знайденого еліпсоїда, для цього виконуємо перетворення координат:
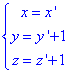
заміна координат
Звідси нові координати

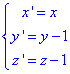
підставляємо в початкове рівняння
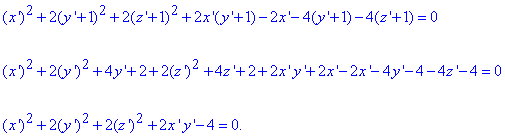
поверхня другого порядку
Останнє рівняння описує еліпсоїд в системі координат, що переміщена в центр еліпсоїда.
Багатьом з Вас готові відповіді на поверхні другого порядку стануть простою інструкцією з обчислень, іншим допоможуть зрозуміти теоретичний матеріал, в будь-якому разі матеріал піде Вам на користь.
Більше подібних матеріалів шукайте на сторінках сайту, тут добре описано поширені навчальні матеріалу для студентів математичних дисциплін.

]]> [email protected] (Yukhym Roman) Поверхні другого порядку Sun, 02 Oct 2016 18:05:15 +0300 Тип поверхні другого порядку. Задачі https://yukhym.com/uk/poverkhni2/typ-poverkhni-druhoho-poriadku-zadachi.html https://yukhym.com/uk/poverkhni2/typ-poverkhni-druhoho-poriadku-zadachi.html В головній публікації практикуму з аналітичної геометрії наведено задачі з визначення, що собою являє поверхня другого порядку та знаходження центру поверхні. В цій та наступних публікаціях наведено аналіз більшої кількості прикладів з поясненням можливих схем їх обчислень. Що краще та швидше вибирати повинні Ви, тому перегляньте завдання та оберіть свій алгоритм їх вирішення.

Задач на визначення типу поверхні

Задача 6.2.1 Визначте тип поверхні другого порядку:
б) x2-y2+3z2-6x+6z+3=0.
Розв'язання: Доповнюємо рівняння та виділяємо повні квадрати
x2-6x+9-y2+3z2+6z+3-9-3+3=0;
(x-3)2-y2+3(z+1)2=32.
Залишилося знормувати отриману залежність на праву частину від знаку рівності і отримаємо

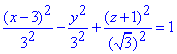
однополий гіперболоїд (витягнутий вздовж осі Oy) з центром O(3;0;-1) і півосями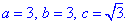
Чому саме такий гіперболоїд - проаналізуйте кінцеве рівняння та співставте висновки, або ж заново беріться за теорію поверхонь дргого порядку.

 

Задача в) З'ясувати тип поверхні другого порядку:
x2-z2-2x+6z-8=0.
Розв'язання: Перегруповуємо доданки та виділяємо повні квадрати
x2-2x+1-z2+6z-9-1+9-8=0;
(x-1)2-(z-3)2=0.
Далі до рівняння застосовуємо формулу різниці квадратів
(x-1+z-3)(x-1-z+3)=0;
(x+z+4)(x-z+2)=0.
Таким чином початкова залежність розщеплються на два рівняння площини
x+z+4=0;
x-z+2=0,
 що перетинаються по дійсній прямій.
Це і є шуканий тип поверхні. У всіх випадках, коли в початковій формулі замасковано рівняння площин схема перетворень буде ідентична, то ж просто один раз її вивчіть.



Задача г) Яка поверхня задана рівнянням:
x2+2y2+3z2-6z+3=0.
Розв'язання: Зведемо до канонічного вигляду дане рівняння, для цього виділимо повний квадрат при "z".
x2+2y2+3z2-6z+3-3+3=0;
x2+2y2+3(z-1)2=0.
На цьому у багатьох студентів перетворення заходять в глухий кут. Але це не правильно, потрібно множники при змінних загнати в знаменник. Для цього 2 і 3 представимо як 1/2, 1/3 в знаменнику, при цьому останнє рівняння набуде вигляду

Отримали уявний конус.

Задача д) Звести до канонічного вигляду поверхню другого порядку:
xy+3z2-18z+54=0.
Розв'язання: Маємо новий тип рівнянь, який за попередньою методикою звести до повних квадратів не вдасться. Зведемо поверхню другого порядку до канонічного вигляду методом Лагранжа.
Суть методу полягає в заміні змінних:

При цьому неважливо в якому порядку позначатимемо змінні, тобто варіант
x=x'-y';
y=x'+y'
також приведе до правильного кінцевого рівняння.
Нові змінні підставляємо в початкову рівняння поверхні другого порядку
(x'+y')(x'-y')+(3z')2-18z'+54=0.
Вже з цього запису Ви можете бачити, для чого застосовували заміну змінних?
Вона дозволяє від добутку змінних перейти до різниці квадратів нових змінних, а рівняння поверхні другого порядку при цьому перетвориться до вигляду
(x')2-(y')2+(3z')2-18z'+27-27+54=0.
Тут додали та відняли 27, щоб виділити повний квадрат при змінній z'.
Рівняння набуде вигляду
(x')2-(y')2+3(z'-3)2-18z'=-27.
Далі нормуємо обидві частини на 27, та зносимо трійку при (z'-3) в знаменник.
В результаті

отримали канонічне рівняння двополого гіперболоїда.
Рівняння двополого гіперболоїда в системі координат Oxy має вигляд:
xy+3(z-3)2=-27.
Якщо Ви зрозуміли наведений алгоритм, то вважайте, що ще одна частина задач на рівняння поверхні другого порядку Вам під силу.
Для закріплення отриманих знань розглянемо подібні рівняння поверхонь.


Задача е) Визначте тип поверхні другого порядку:
xz-6z+3=0.
Розв'язання: Як і в попередньому приладі, при зведенні до канонічного вигляду застосовуємо метод Лагранжа.
Для цього зробимо заміну змінних:

Перепишемо рівняння поверхні
(x'+z')(x'-z')-6(x'-z')+3=0.
Отримали різницю квадратів
(x')2-(z')2-6x'+6z'+3=0;
(x')2-6x'+9-(z')2+6z'-9+3=0;
(x'-3)2-(z'-3)2=-3.
При нормуванні рівняння поверхні на (-3) отримаємо

канонічне рівняння гіперболічного циліндра.
Повторна заміна змінних

дає запис

який є канонічним рівняння гіперболічного циліндра в канонічній системі координат

Гіперболічний циліндр в декартовій системі координат Oxy матиме вигляд:
(x-6)z=-3,
його вісь паралельна осі Oy.



Задача є)Звести до канонічного вигляду поверхню:
yz+4x-6y+12z+25=0.
Розв'язання: З вигляду поверхні робимо висновок, що потрібно застосувати метод Лагранжа.
Заміна змінних вперед:

та назад
(*)
Тоді вихідне рівняння перетворимо до наступного
(y'+z')(y'-z')=4x'-6(y'+z')+12(y'-z')+25=0;
(y')2-(z')2+4x'-6y'-6z'+12y'-12z'+25=0.
Далі доповнюємо квадратичні залежності до повних квадратів
(y')2-6y'+9-(z')2-18z'-81-9+81+4x'+25=0;
(y'+3)2-(z'+9)2=-4(x'+24,5).(**)
 Незвичне рівняння, яке ще потрібно перетворювати.
Для цього робимо заміну:

Зворотній перехід, враховуючи (*) буде мати вигляд

Тоді рівняння поверхні (**) зведеться до
(y'')2-(z'')2=-4x''.
канонічного рівняння гіперболічного параболоїда в канонічній системі координат.



Задача ж) Який тип має поверхня другого порядку?
x2+4xz-4z2-6z+3=0.
Розв'язання: Тут можна застосовувати метод Лагранжа, а можна обійтись і без нього. Для цього перші два доданки доповнимо до повного квадрату і те ж саме виконаємо з частиною рівняння поверхні, що залишиться.
В результаті математичних перетворень матимемо

Такий запис легко читати, проте ще одна заміна змінних

перетворює рівняння поверхні до

канонічного рівняння гіперболічного циліндра.
Цих завдань цілком вистачає, щоб навчитися обчислювати завдання подібного типу.

Більше прикладів на зведення поверхні другого порядку до канонічного вигляду та з'ясування її типу в наступній публікації.

]]> [email protected] (Yukhym Roman) Поверхні другого порядку Sun, 02 Oct 2016 18:21:16 +0300 Центр поверхні другого порядку. Задачі https://yukhym.com/uk/poverkhni2/centr-poverhni-2-poryadku.html https://yukhym.com/uk/poverkhni2/centr-poverhni-2-poryadku.html Продовжуємо цикл статтей з дослідження поверхонь другого порядку. Цього разу будемо аналізувати відповіді до завдань на знаходження центру поверхонь. Наведені приклади досить поширені, тому матеріал побудовано та, що після першого ознайомлення Ви самостійно змогли знайти правиьну відповідь.

Задачі на знаходження центру поверхні

Задача 6.3.1 б) Знайдіть центр поверхні другого порядку:
3x2-2y2+z2+2xy-2xz+8yz+4x+6y-12z-1=0
Розв'язання: Записуємо коефіцієнти рівняння поверхні другого порядку:
a11=3, a22=-2, a33=1, a12=1, a13=-1,a23=4, a14=2, a24=3,a34=-6,a44=-1.
Далі з їх допомогою складаємо систему трьох рівнянь для знаходження центру поверхні другого порядку.
Перетворюємо СЛАР методом Гауса:

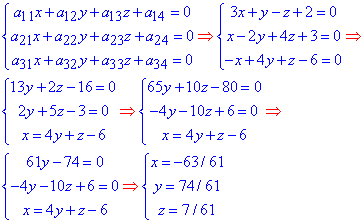
В результаті центром поверхні буде точка O(-63/61;74/61;7/61).

 

Задача в) Визначте координати центру поверхні другого порядку:
4x2+2y2+12z2-4xy+12xz+8yz+14x-10y+7=0.
Розв'язання: Знайдемо центр поверхні другого порядку (ПДП), взявши часткові похідні за правмлом

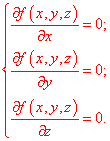
Для багатьох із Вас ця формула буде набагато корисніша і швидша, порівняно з виписуванням коефіцієнтів з рівняння поверхні та складання СЛАР.
Система рівнянь при обчисленні часткових похідних набуде вигляду

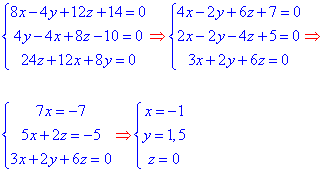
Після її зведення до східчастого вигляду розв'язуємо, в результаті можемо записати центр поверхні O(-1;1,5;0) у відповідь.

 

Задача г) Знайдіть геометричне мысце координат центру поверхні другого порядку:
5x2+9y2+9z2-12xy-6xz+12x-36z=0.

Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку:
a11=5, a22=9, a33=9, a12=-6, a13=-3,a23=0, a14=6, a24=0,a34=-18,a44=0.
Знайдемо центр поверхні другого порядку (ПДП) із СЛАР:

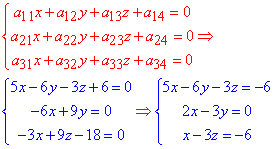
Систему рівнянь розв'яжемо методом Гауса, для цього складемо розширену матрицю системи лінійних рівнянь і зведемо до східчастого вигляду: третій рядок міняємо з першим місцями, далі утворюємо нулі під першим елементом - для цього від другого рядка віднімаємо подвоєний перше, а від третього віднімаємо перший помножений на (5). Далі 2 і 3 рядок нормуємо на (-3), після чого від 3 віднімаємо подвоєний 2.

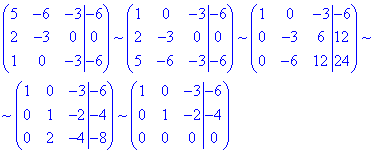
Оскільки ранг матриці r=2<3, то розв'язок системи рівнянь буде не точка, а пряма, яка є перетином площин, утвореної із останньої розширеної матриці:
x-3z+6=0;
y-2z+4=0.
Запишемо рівняння прямої в канонічному вигляді. Для цього знайдемо напрямний вектор площини і точку, що належить прямій. Напрямний вектор прямої в просторі p – це векторний добуток двох нормальних векторів площин n1(1;0;-3) і n2(0;1;-2), що утворюють пряму при перетині (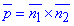). Векторний добуток знаходимо через визначник складений за формулою

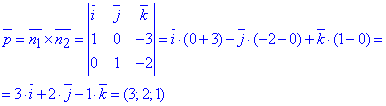
Знайдемо точку, що належить прямій (в просторі), нехай x=0, тоді підстановкою в рівняння площин знаходимо дві невідомі координати точки на прямій:

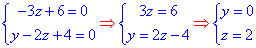
Таким чином маємо точку прямої M(0;0;2).
Маємо все дя того, щоб скласти канонічне рівняння прямої центрів заданої поверхні другого порядку: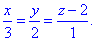

Уважно перегляньте, як було складене рівняння прямої, щоб наступного разу змогли повторити подібні обчислення.

 

Задача д) Знайдіть центр поверхні другого порядку:
5x2+2y2+2z2-2xy+2xz-4yz-4y-4z+4=0.
Розв'язання: З рівняння поверхні виписуємо коефіцієнти рівняння:
a11=5, a22=2, a33=2, a12=-1, a13=1,a23=-2, a14=0, a24=-2,a34=-2,a44=4.
Для знаходження центр поверхні другого порядку складаємо систему рівнянь: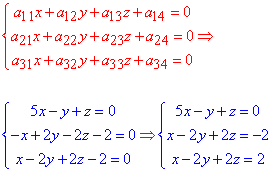

Її розв'яжемо методом Гауса, для цього випишемо розширену матрицю СЛАР і зведемо до східчастого вигляду: 5 і 1 рядок міняємо місцями і занулюємо елементи під першим.

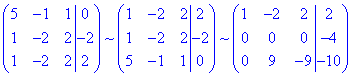
З другого рядка матриці робимо висновок, що система лінійних рівнянь несумісна, тому задана ПДП центра не має. Якщо б замість (-4) в правій частині мали нуль, то необхідно б було за методикою попереднтого прикладу знайти пряму перетину площин. Проте маємо несумісну СЛАР, що спрощує подальші обчислення і дозволяє зробити висновок що поверхня другого порядку не має центру.

 

Задача е) Визначте центр поверхні другого порядку:
x2-2y2+z2+6yz-4xz-8x+10y=0
Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку :
a11=1, a22=-2, a33=1, a12=0, a13=-2,a23=3, a14=-4, a24=5,a34=0,a44=0.
Знайдемо центр поверхні другого порядку (ПДП), розв'язавши СЛАР:

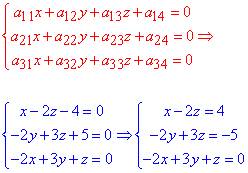
Систему рівнянь розв'яжемо методом Гауса, для цього складемо розширену матрицю системи лінійних рівнянь і зведемо її до східчастого вигляду:

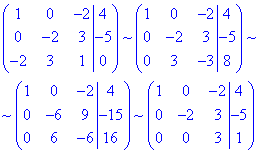
отримали трикутну систему рівнянь:

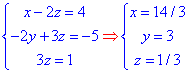
з якої знаходимо O(14/3; 3;1/3) - центр поверхні другого порядку.



Задача є) Знайдіть центр поверхні другого порядку:
4x2+y2+9z2-4xy+12xz-6yz+8x-4y+12z-5=0
Розв'язання: Центр поверхні знаходимо за алгоритмом, який добре розписаний в попередніх завданнях. Спершу запишемо коефіцієнти при рівнянні ПДП:
a11=4, a22=1, a33=9, a12=-2, a13=6,a23=-3, a14=4, a24=-2,a34=6,a44=-5.
Знайдемо центр поверхні другого порядку із СЛАР:

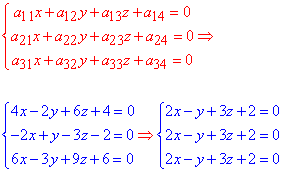
Із кінцевих співвідношень бачимо, що маємо три ідентичні рівняння тому робимо висновок, що задана поверхня другого порядку має площину центрів:
2x-y+3z+2=0.
Такі результати також можливі на практиці.

 

Задача ж) Знайдіть центр поверхні другого порядку:
x2+4y2+5z2+4xy-12x+6y-9=0
Розв'язання:Коефіцієнти рівняння поверхні другого порядку рівні:
a11=1, a22=4, a33=5, a12=2, a13=0, a23=0, a14=-6, a24=3, a34=0, a44=-9.
Центр поверхні другого порядку (ПДП) знаходимо із системи трьох рівнянь, яку складаємо з допомогою виписаних коефіцієнтів:

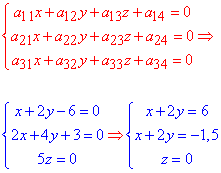
Отрима два рівняння, права частина яких відрізняється. Одночасно це неможливо, оскільки 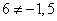, тому робимо висновок, що система рівнянь несумісна, і відповідно поверхня не має центра.

Задача з) Знайдіть центр поверхні другого порядку:
3x2+2y2+4yz-2xz-2x-8z-8=0
Розв'язання: Випишемо коефіцієнти рівняння заданої поверхні другого порядку:
a11=3, a22=2, a33=0, a12=0, a13=-1, a23=2, a14=-1, a24=0, a34=-4, a44=-8.
З коефіцієнтів складаємо рівняння на визначення центру поверхні другого порядку (ПДП):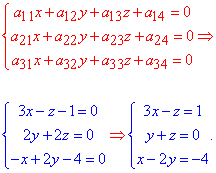

Систему рівнянь обчислюємо методом Гауса, для цього виписуємо розширену матрицю системи лінійних рівнянь і поступово спрощуємо її, щоб отримати східчастий вигляд:

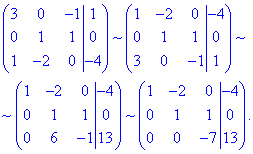
Далі в зворотньому порядку визначчаємо координати

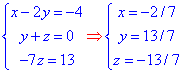
Звідси точка O(-2/7;13/7;-13/7) - центр ПДП.

 

Задача і) Знайдіть центр поверхні другого порядку:
x2+25y2+9z2-10xy+6xz-30yz-2x-2y=0
Розв'язання: З рівняння поверхні виписуємо коефіцієнти
a11=1, a22=25, a33=9, a12=-5, a13=3, a23=-15, a14=-1, a24=-1, a34=0, a44=0.
Складаємо систему трьох лінійних рівнянь, розв'язок якої і буде центром поверхні другого порядку (ПДП):
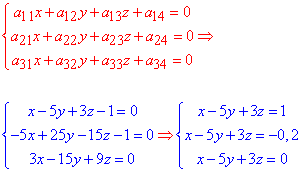
знаходження центру поверхні
З аналізу 1 і 3 рівняння бачимо, що система рівнянь несумісна, оскільки 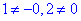, а це означає що поверхня не має центра.

 

Задача ж) Знайдіть центр поверхні другого порядку:
x2-14y2+10z2-4xy+6xz-24yz+2x+20y+8z-9=0.
Розв'язання: Щоб закріпити другий метод, який розглядали вище, знайдемо центр поверхні, взявши часткові похідні за формулою:
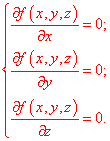
система диф. рівнянь
В результаті диференціювання отримаємо систему лінійних рівнянь, яку методом Гауса зводимо до східчастої
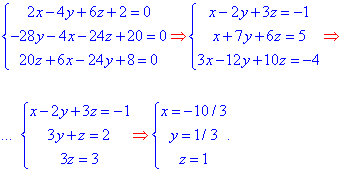
центр поверхні
Звідси O(-10/3;1/3;1) - центр поверхні другого порядку.
Замість «…» зробили елементарні перетворення системи рівнянь, які можете повторити самостійно.
Наведені приклади служитимуть Вам доброю інструкцією з обчислення завдань на центр поверхні.
Збережіть матеріал в закладках та діліться посиланням на корисний матеріал з друзями.

]]> [email protected] (Yukhym Roman) Поверхні другого порядку Tue, 04 Oct 2016 06:53:17 +0300 Діаметральна площина поверхні другого порядку https://yukhym.com/uk/poverkhni2/diametralna-ploshchyna-poverkhni-druhoho-poriadku.html https://yukhym.com/uk/poverkhni2/diametralna-ploshchyna-poverkhni-druhoho-poriadku.html Відрізок, який сполучає дві довільні точки поверхні другого порядку (ПДП), називається хордою цієї поверхні. 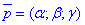Множина середин хорд ПДП паралельних до неасимптотичного напряму  утворює площину, яку називають діаметральною площиною поверхні другого порядку. Таким чином діаметральна площина, це площина що спряжена з напрямом 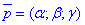нормаль , а її рівняння наступне:

рівняння діаметральної площини
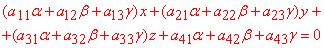
Теорема: Всі діаметральні площини проходять через центр поверхні 2 порядку!

Хто навчається в Львівському національному університеті імені Івана Франка, той може знайти готові відповіді до практикуму з аналітичної геометрії.
Наступні приклади задавали на кафедрі геометрії і топології  механіко-математичного факультету при вивченні вказаних далі тем:

Розділ VI: «Поверхні другого порядку».
Частина IV: «Діаметральні площини »


Приклад 6.4.1 Знайдіть діаметральну площину поверхні 3x2+2y2-z2+3xy-2yz+7=0, яка проходить через точки A(-1;2;0), B(3;0;2).
Розв'язання: Оскільки діаметральна площина проходить через центр ПДП, то спершу знайдемо координати центра. Для цього випишемо коефіцієнти рівняння поверхні другого порядку:
a11=3, a22=2, a33=-1, a12=1.5, a13=0,a23=-1,a14=0, a24=0,a34=0,a44=7.
Хто не знає як, то співставте значення aij з рівнянням або перегляньте попередніуроки з поверхонь.
Коефіцієнти потрібні для побудови системи трьох лінійних рівнянь, обчисення якої дає центр поверхні другого порядку:
центр поверхні другого порядку 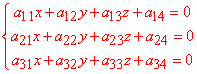Формула є досить простою, а СЛАР в багатьох випадках близька до трикутної форми.
Лише в окремих випадках Вам доведеться застосувати метод Гауса, щоб звести систему рівнянь до східчастого вигляду
Отож складаємо рівняння та обчислюємо
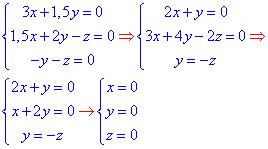система рівнянь Знайшли точку O(0;0;0) - центр поверхні ПДП.
Наступним кроком складаємо рівняння площини, яка проходить через три точки A(-1;2;0), B(3;0;2), O(0;0;0):
для цього застосовуємо формулу визначника
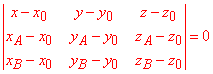поверхня через визначник Розкладемо визначник через мінори першого рядка
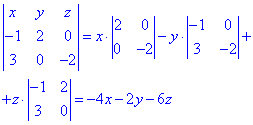знаходження діаметральної площини Цей метод досить зрозумілий і ефективний, оскільки залишається знайти визначники 2 порядку. В іншому випадку Вам би довелося групувати сталі та коеф. при змінних.
Розділимо праву частину на двійку та прирівняємо до нуля.
Таким чином, ми знайшли рівняння діаметральної площини:
2x+y+3z=0.
Даним алгоритм використовуйте в завданнях, які мають ідентичну умову. Далі будуть розглянуті більш складні в плані обчислень приклади на діаметральні площини.

 

Приклад 6.4.2 Знайдіть діаметральну площину поверхні 2x2-y2+z2-4x+4z+3=0, яка проходить через точки A(0;-2;1), B(2;-3;0).
Розв'язання: Спершу необхідно визначити координати центру поверхні другого порядку.
Запишемо коефіцієнти рівняння ПДП, які необхідні для складання системи лінійних рівнянь:
a11=2, a22=-12, a33=1, a12=0, a13=0,a23=0,a14=-2, a24=0,a34=2,a44=3.
Складаємо СЛАР та визначаємо

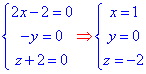
центр поверхні другого порядку (ПДП) -O(1;0;-2).
Побудуємо рівняння площини, яка проходить через три точки A(0;-2;1), B(2;-3;0), O(1;0;-2).
Детермінант запишемо формулою
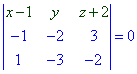визначник Знаходимо визначник через алгебраїчні доповнення до першого рядка
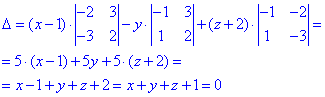Рівняння шуканої діаметральної площини має вигляд:
x+y+z+1=0.
На цьому завдання розв'язано.

 

Приклад 6.4.3 Знайдіть діаметральну площину поверхні x2-z2+2xy-yz+3y+5=0, яка перпендикулярна до прямої (x+5)/1=(y-1)/2=z/0
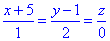
рівняння прямої
Розв'язання: Записуємо коефіцієнти рівняння заданої поверхні другого порядку:
a11=1, a22=0, a33=-1, a12=1, a13=0,a23=-0.5,a14=0, a24=1.5,a34=0,a44=5.
Повторно наведемо рівняння діаметральної площини, яка паралельна до деякого неасимтотичного напряму 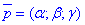в загальному вигляді:

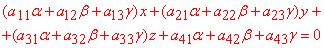
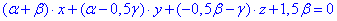діаметральна площина (*)
Отримали рівняння площини з нормальним вектором:
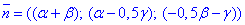вектор нормалі Оскільки шукана площина перпендикулярна до заданої прямої (з напрямним вектором 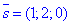), то за властивістю колінеарності 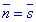прирівнюємо значення координат.
В результаті отримаємо систему трьох рівнянь
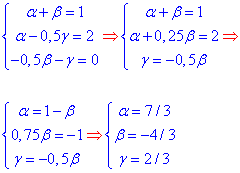з якої знаходимо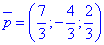 нормаль
Підставимо координати вектора 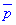у рівняння (*) шуканої площини, отримаємо рівняння діаметральної площини x+2y-2=0.

 

Приклад 6.4.4 Знайдіть діаметральну площину поверхні y2+z2+2xy+3yz-3y-7=0, яка перпендикулярна до прямої x/(-2)=(y+3)/(-1)=(z-4)/1
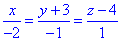
пряма
Розв'язання: Уважно виділяємо коефіцієнти рівняння поверхні:
a11=0, a22=1, a33=1, a12=1, a13=0,a23=1.5,a14=0, a24=-1.5,a34=0,a44=-7.
Загальне рівняння діаметральної площини, що паралельна до неасимтотичного напряму 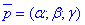задаєься формулою:
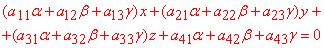формула діаметральної площини При підстановці отримаємо
(**)
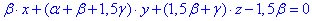Рівняння діаметральної площини матиме нормальний вектор, координати якого є множниами при змінних в тільки що висаному рівнянні:
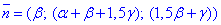Далі за умовою, що шукана площина є перпендикулярною до заданої прямої (з напрямним вектором 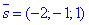, то за властивістю вектори колінеарні: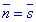
Прирівнюємо їх значення та визначаємо alpha, beta, hamma:
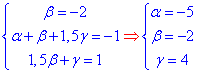Нормальний вектор дыаметральноъ площини має координати .
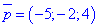Підставимо знайдені значення 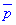у рівняння (**), в резуьтаті отримаємо рівняння діаметральної площини -2x-y+z+3=0, або після множення на (-1) у вигляді
2x+y-z-3=0.

 

Приклад 6.4.5 Запишіть рівняння тієї діаметральної площини для поверхні
4x2+4y2+12z2-10xy+4yz+4xz-16x-16y+16z-3=0,
яка паралельною до площини x+2y-3z+5=0.
Розв'язання: Коефіцієнти рівняння поверхні рівні:
a11=4, a22=4, a33=12, a12=-5, a13=2,a23=2,a14=-8, a24=-8,a34=8,a44=-3.
Записуємо загальну формулу рівняння діаметральної площини:
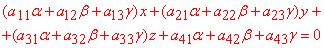та з урахуванням aij
(***)
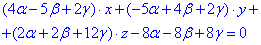Нормальний вектор пощини матиме координати:

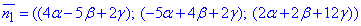
Оскільки невідома діаметральна площина паралельна до заданої в умові площини x+2y-3z+5=0
(з нормальним вектором 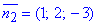), то з умови паралельності маємо: n1=n2.
Із системи 3 інійних рівнянь виражаємо alpha, beta, hamma
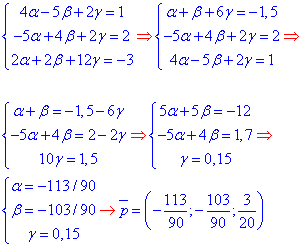та підставяємо у рівняння діаметральної площини (***)
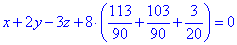знаходження площини або x+2y-3z+20,4=0.
Після трьох проаналізованих завдань думаю Ви готові обчислити такого видуу завдання самостійно.

 

Приклад 6.4.6 Запишіть рівняння тієї діаметральної площини для поверхні
4x2+4y2+12z2-10xy+4yz+4xz-16x-16y+16z-3=0,
яка є паралельною до площини 2x+y-z+1=0.
Розв'язання: Можливо для когось це буде зайвим проте повторюваність одного і того рано чи пізно приводить до закріплення матеріалу. Тому пройдемося по схемі обчислень на прикладі ще двох рівнянь ПДП.
Першим кроком записуємо коефіцієнти рівняння поверхні:
a11=4, a22=4, a33=12, a12=-5, a13=2,a23=2,a14=-8, a24=-8,a34=8,a44=-3.
Далі за формулою
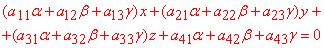складаємо рівняння діаметральної площини в коефіцієнтах нормального вектора
(****)
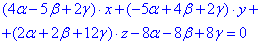Виписуємо координати нормалі:
координати нормалі 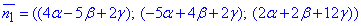та за умовою паралельності до площини 2x+y-z+1=0, що задана початковою умовою, прирівнюємо їх до нормального вектора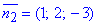
Звідси отримаємо систему трьох лінійних рівнянь
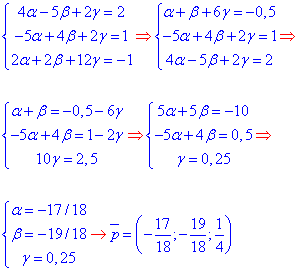обчислення СЛАР обчислення якої і дає alpha, beta, hamma.
Підставимо координати вектора 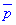у рівняння діаметральної площини
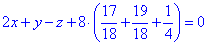діаметральна площина після спрощень отримаємо
2x+y-z+18=0.

 

Задача 6.4.7 Запишіть рівняння тієї діаметральної площини для поверхні
2x2-5y2-3z2-2xy-4xz+2yz-2x-10y-2z-1=0, яка є перпендикулярною до осі ординат.
Розв'язання: Переходимо до розрахунків - спершу aij:
a11=2, a22=-5, a33=-3, a12=-1, a13=-2,a23=1,a14=-1, a24=-5,a34=-1,a44=-1.
Рівняння діаметральної площини, яка паралельна до деякого неасимтотичного напряму 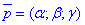після підстановки в формулу:
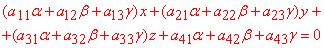спроститься до вигляду
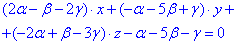Оскільки вісь ординат має напрямний вектор p(0;1;0), то за властивістю паралельності нормальних векторів маємо:
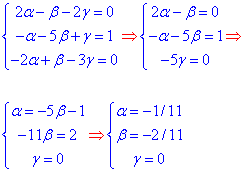розв'язування СЛАР Підставляємо координати (alpha; beta; hamma) у рівняння діаметральної площини

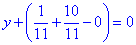
та спрощуємо
y+1=0.

Знання легко не даються, для закріплення матеріалу постійно розв'язуйте по декілька однотипних прикладів на розгянуті умови.
Робіть практичні до тих пір, поки повністю не запам'ятаєте схему розрахунків.
Удачі Вам на практичних та екзаменах!

]]> [email protected] (Yukhym Roman) Поверхні другого порядку Fri, 07 Oct 2016 08:24:23 +0300 Центр поверхні другого порядку. Заміна системи координат https://yukhym.com/uk/poverkhni2/poverkhni-2-poriadku-zamina-sk.html https://yukhym.com/uk/poverkhni2/poverkhni-2-poriadku-zamina-sk.html Завдання на перенесення початку координат вимагають знань всього попереднього матеріалу, тому якщо Ви почали читати цю статтю і багато чого не розумієте, тоді реомендуємо ознайомитися з попередніми публікаціями. Тут Вам також стануть в нагоді знання систем координат, а саме як правильно виконати паралельний перенос. Проанізуйте відповіді і навчіться обчислювати завдання на переніс центру поверхні.

Задача 6.3.2 б) Перенесіть початок координат в центр поверхні другого порядку:
y2+3xy+xz+2yz+3x+2y=0;
Розв'язання: Цей та наступні приклади дозволять Вам самостійно опанувати методику знаходження центру поверхні.
Спершу виписуємо коефіцієнти рівняння заданої поверхні другого порядку:
a11=0, a22=1, a33=0, a12=1.5, a13=0.5, a23=1, a14=1.5, a24=1, a34=0, a44=0.
Як правильно виписати оефіцієнти описано в попередніх публікаціях.
Будуємо систему рівнянь та методом Гауса зводимо її до східчастої: СЛАР
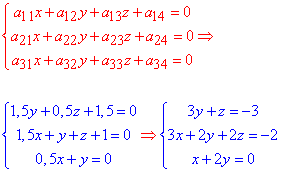
Звідси отримаємо центр поверхні другого порядку

Перенесемо початок координат в центр O(0,8; -0,4;-1,8), необхідна заміна координат наступна
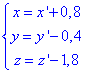
заміна змінних
Звідси нові координати в старій системі

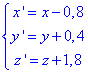
Підставляємо їх в рівняння поверхні та знаходимо шукану відповідь
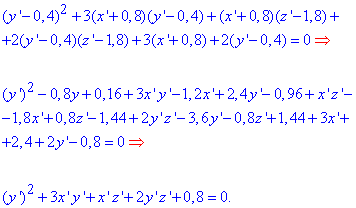
заміна рівняння поверхні
Хід трансформації рівняння поверхні до нових координат можете прослідкувати з аналізу наведених формул.

Задача в) Перенесіть початок координат в центр поверхні другого порядку: x2+2y22-z2+2x-4y+2z+1=0.

Розв'язання: Дотримуємося наведеної інструкції і з практикою, що раз швидше зможете виконувати подібні вправи.
З рівняння поверхні виписуємо коефіцієнти при змінних:
a11=10, a22=2, a33=-1, a12=0, a13=0, a23=0, a14=15, a24=-2, a34=1, a44=1.
Правильно виписані значення - це половина правиьної відповіді, тому, якщо Вам тяжко зрозуміти звідки їх беремо, оді краще застосовуйте формули часткових похідних по змінних.
І в першому, і в другому випадку Ви прийдете до системи трьох рівнянь з трьома невідомии:
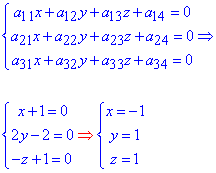
система рівнянь
Як її обчислювати залежить від Ваших вподобань, проте в більшості випадків сам запис СЛАР підкаже, що далі з ними робити.
В цьому завданні система проста, тому легко знаходимо центр поверхні -O(-1;1;1).
Далі виписуємо заміну координат, яка перенесе початок координат в центр поверхні - точку O:
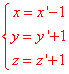
заміна координат
Звідси перехід від нових координат до попередніх має вигляд

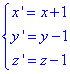
Підставляємо заміну змінних та розписуємо рівняння поверхні в якої центр співпадає з початком координат
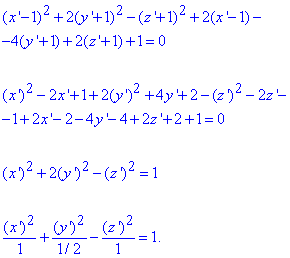
рівняння поверхонь
Отримали канонічне рівняння однополого гіперболоїда (поверхня обертання).
Думаю, що більшість наведених прикладів допоможуть Вам вправніше вирішувати практичні завдання, не мати страху на екзаменах та контроьних.

]]> [email protected] (Yukhym Roman) Поверхні другого порядку Tue, 04 Oct 2016 07:04:13 +0300