Означення числової послідовності: Множину чисел
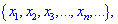
яка визначена для кожного натурального числа за однаковим правилом називають числовою послідовністю і позначають {xn}, де x1,x2,x3,... – члени числової послідовності, xn– загальний член послідовності.Означення границі послідовності: Число a називається границею числової послідовності {xn}, якщо для будь-якого як завгодно малого додатного числа
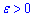знайдеться таке натуральне число 
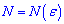, таке що при всіх n>N виконується нерівність
Якщо a є границею послідовності то записують
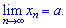
Є декілька типів числових послідовностей, які ви обов'язково повинні знати:
1) Зростаюча послідовність – кожен її член більший від попереднього
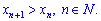
2) Неспадна послідовність – кожен наступний член не менший від попереднього
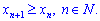
3) Спадна послідовність – кожен новий член менший за попередній
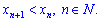
4) Незростаюча послідовність – кожен старший член не більший за попередній
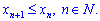
5) Обмежена послідовність має місце тоді, коли знайдуться такі дійсні числа m і M, що для всіх натуральних чисел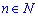 
виконується нерівність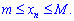 
6) Послідовність {xn} називається необмеженою, якщо вона постійно або зростає або спадає.
7) Послідовність, що має границю називається збіжною. Протилежна до неї послідовність – відповідно розбіжною.
ВЛАСТИВОСТІ ЗБІЖНИХ ПОСЛІДОВНОСТЕЙ
1) Границя сталої послідовності рівна сталій.
2) Якщо послідовність має границю, то границя єдина. Звідси слідує, що така послідовність обмежена.
3) Нехай границя числової послідовності існує і рівна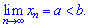
Тоді знайдеться таке число N, що для всіх більших за нього значень n>N виконується нерівність xn<b.
4) Припустимо, що виконується нерівність
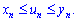
Якщо послідовності {xn} та {yn} збіжні та їх границі рівні
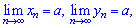
то послідовність {un} також буде збіжною, а її співпадатиме з границями бокових послідовностей
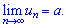
5) Будь-яка монотонно обмежена послідовність має границю.
Частковим випадком числових послідовностей є арифметична та геометрична прогресії.
Одними з простих завдань є визначення формули загального члена послідовності за відомими першими. Для прикладу, виберемо такі задачі із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Написати формулу загального члена послідовності.
1) (4. 258)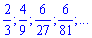 
Розв'язок. При визначенні загального члена послідовності слід вловити особливість зміни наступного його члена до попереднього. Різниця між ними може носити лінійний, показниковий чи інший характер. В даному випадку приклади не важкі, оскільки кожен наступний член описаний в тому вигляді, в якому його визначають, а не у вигляді дробу (в чисельнику і знаменнику одне число). Варто зазначити те, що при виведенні загального члена послідовності прийнято записувати першими змінні n, тобто у вигляді
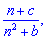
а не
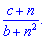
Перейдемо до знаходження шуканих величин.
З особливості зміни чисельника і знаменника
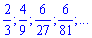
бачимо, що чисельник зростає лінійно, а знаменник за показниковим законом.
Загальний член послідовності записуэмо формулою
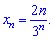
В чисельнику отримали лінійну залежність, знаменнику - показникову.
2) (4. 261)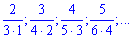 
Розв'язок. В цьому завданні і чисельник і знаменник змінюються лінійно, зміщуючись від одиниці на певні константи. Тільки в знаменнику маємо добуток чисел, тому в формлі загального члена
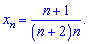
це виражається квадратичною залежністю.
3) (4. 265)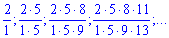 
Розв'язок.В даному прикладі зміна чисельника та знаменника є нелінійною, проте загальний член послідовності вловити можна.
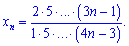
Для знаходження формули загального члена послідовності дослідіть поведінку окремо чисельника та знаменника. Визначте чи вони змінюються лінійно, нелінійно, степенево і т.д. На основі закономірностей виведіть формулу загального члена послідовності. Це вся інструкція при виведенні формули загального члена послідовності. Спочатку буде важкувато, зато пысля вправлянь будете малювати загальний член як художни картину.
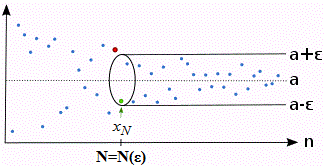
Якщо a є границею послідовності то цьому відповідає запис
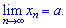
Обчислення границі числової послідовності
Приклад 1 Легке завдання, яке вчить виносити домінантні множники, котрі дають найбільший вклад при номері прямуючому до безмежності, в дробах та спрощувати на них
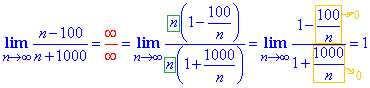
Якщо послідовність збіжна, то вона має скінченну границю. Якщо границя рівна безмежності, то така послідовність є розбіжною.
Для встановлення збіжності послідовностей потрібно добре вміти знаходити границі, що ми з Вами постійно вдосконалюємо.
Приклад 2 Маємо невизначеність виду безмежність мінус безмежність (∞-∞), тому теорему про різницю границь тут застосовувати не можна. Перетворимо вираз, помноженням та діленням на спряжений вираз. Для обчислення значення границі спрощуємо дріб на вираз, що вносить найбільший вклад при аргументі прямуючому до нескінченності. Як виносити множники з пд кореня Ви повинні навчитися самостійно, без цього важко буде розкривати границі з коренями.
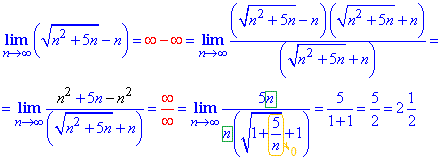
Приклад 3 Різницю коренів в знаменнику дробу не домножуємо на спряжений вираз, а просто номер n виносимо з під кореня (уважно перегляньте як це робити), а далі спрощуємо з n виділеним в чисельнику
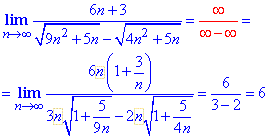
Приклад 4 Послідовність із частки ірраціональних виразів має скінченну границю, якщо степінь номера n в знаменнику рівний степені в чисельнику (або більший). Його виділяємо за вказаною в формулі методикою, та спрощуємо
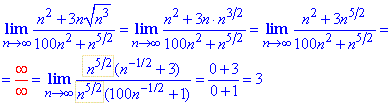
Приклад 5 Знайти границю послідовності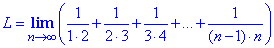 
Обчислення: Проаналізувавши, як змінюються доданки для всіх номерів k=2,3,4 можна записати формулу
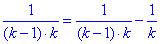
Таким чином вихідну суму зводимо до вигляду
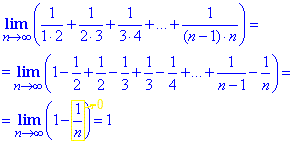
Єдиного усталеного алгоритму, як розкривати такі суми немає. Деколи можна побачити прості схеми чередування доданків, в інших завданнях буває потрібно обчислюваити суми арифметичних чи геометричних прогресій. Лиш би оцінити зверху, що послідовність обмежена, та до якого значення прямує.
Приклад 6 Ліміт послідовності із частки показникових виразів обчислюють шляхом виділення і спрощення домінантних множників в чисельнику та знаменнику дробу. В заданій границі основи рівні 2 та 4, їх можна звести до спільної 4 в (найвищому) степені рівному n. Все решта і дасть значення до якого прямує дріб.
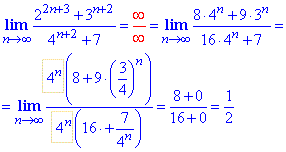
Приклад 7 Границя послідовності з різниці нескінченно великих дробів розкриваємо методом зведення їх до спільного знаменника та спрощення в чисельнику та знаменнику множника, що вносить головний вклад
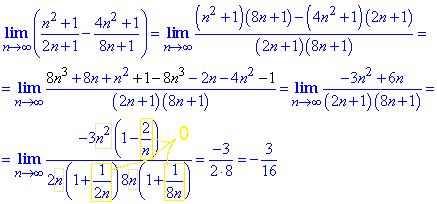
Приклад 8 Знайти ліміт послідовності
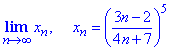
Обчислення: Представимо загальний член послідовності {xn} у вигляді
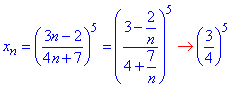
За теоремою про границю показникової функції, вона рівна показнику від границі основи, якщо степінь скінченна. Звідси lim{xn}=(3/4)^5.
Приклад 9 В такого сорту винесення n в найвищому степені за дужки в чисельнику та знаменнику дробу до спрощення не призведе. Спробуйте перевірити самостійно, залишається поглянути в формули скороченого множення та розписати різниці та суми в кубі та четвертому степені за наступними формулами
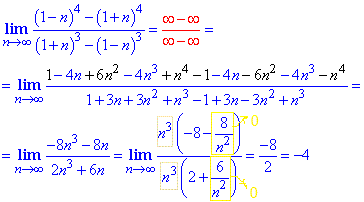
Таким чином отримаємо доданки з протилежними знаками, які в сумі дадуть 0, решта в граничному переході спроститься за наведеною вище методикою.
І наостанок, ще кілька розв'язків на границю послідовності, які пропонуємо розібрати самостійно.
10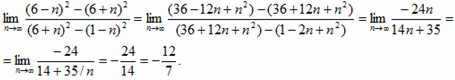 
11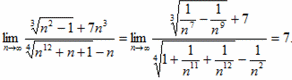 
12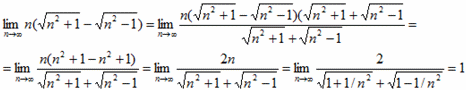 
13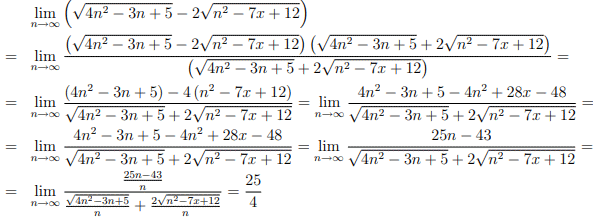 
Переглянути подібні матеріали:
]]>Обчислення границь методом підстановки
Приклад 1. Знайти границю функції
Lim((x2-3*x)/(2*x+5), x=3).
Розв'язання: Такого типу приклади обчислюють звичайною підстановкою
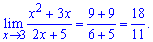
Границя рівна 18/11.
Нічого складного і мудрого в таких границях немає, підставили значення, обчислили, записали границю у відповідь. Зате на базі таких границь всіх привчають, що перш за все потрібно підставити значення у функцію (принаймі перевірити, що отримаємо? чи - до чого прямує границя?).
Далі границі ускладнюють, вводять поняття безмежності, невизначеності і т.д.
Границі з невизначеністю типу безмежність розділити на безмежність. Методи розкриття невизначеності
Приклад 2. Знайти границю функції
Lim((x2+2x)/(4x^2+3x-4), x=infinity).
Розв'язання: Задана границя виду поліном розділити на поліном, причому змінна прямує до безмежності
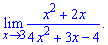
Проста підстановка значення до якого прямує змінна знайти границю не допоможе, отримаємо невизначеність виду безмежність розділити на безмежність.
Алгоритм обчислення границі полягає у знаходженні найбільшого степеня "ікс" в чисельнику чи знаменнику. Далі на нього спрощують чисельник і знаменник і знаходять границю
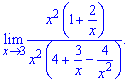
Оскільки значення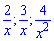 
прямують до нуля при змінній прямуючій до нескінченності то ними нехтують, або записують в кінцевий вираз у вигляді нулів
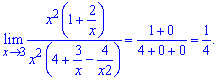
Зразу з практики можна отримати два висновки, які є підказкою в обчисленнях. Якщо змінна прямує до нескінченності і найбільший степінь чисельника перевищує найбільший степінь знаменника то границя рівна нескінченності (+ чи -, знак потрібно уточняти). В протилежному випадку, якщо вираз в знаменнику старшого порядку ніж в чисельнику границя рівна нулю.
Формулами границі можна записати так
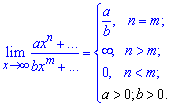
Якщо маємо в границі звичайний поліном без дробів, то границя теж рівна нескінченності
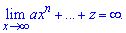
Наступний тип прикладів на границі базується на поведінці функції біля нуля.
Приклад 3. Знайти границю функції
Lim((x^2+3x-5)/(x^2+x+2), x=0).
Розв'язання: Тут вже виносити найстарший доданок полінома не потрібно. З точністю до навпаки, необхідно знайти найменший степінь чисельника і знаменника та тільки їх і врахувати при обчисленні границь
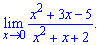
Значення x^2; x прямують до нуля коли змінна прямує до нуля 
Тому ними нехтують, таким чином отримаємо
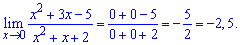
Границя рівна 2,5.
Границі з невизначеністю типу 0/0 і методи їх обчислень
Зразу всі згадують правило, що ділити на нуль не можна. Однак в цьому контексті маємо на увазі безмежно малі функції.
Розглянемо для наочності приклад
Приклад 4. Знайти границю функції
Lim((3x^2+10x+7)/(x+1), x=-1).
Розв'язання: При підстановці у знаменник x=-1 отримаємо нуль, також 0 отримаємо в чисельнику. Отже маємо невизначеність типу 0/0.
Боротися з такою невизначеністю просто: потрібно розкласти квадратний тричлен на множники, а точніше - виділити множник, який перетворює вираз на нуль.
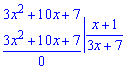
Отже, границю можна записати у вигляді
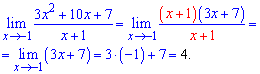
Ось і вся методика. Подбним чином поступаємо, якщо маємо границі частки многочленів третього та вищого степеня.
Приклад 5. Знайти границю функції
Lim((2x^2-7x+6)/(3x^2-x-10), x=2).
Розв'язання: Пряма підстановка показує
2*4-7*2+6=0;
3*4-2-10=0
що маємо невизначеність типу 0/0.
Поділимо квадратний тричлен на множник, що дає особливість
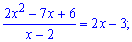
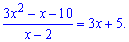
Є практики, які вчать, що многочлени 2 порядку, тобто квадратні тричлени, слід розв'язувати через дискримінант. Але сам факт, що в точці прямим підставленням отримуємо нуль прямо вказує, що вона є розв'язком, іншу дістанемо роздленням вільного члена на неї. Тобто, при "ікс" прямуючому до 2 в чисельнику отримали 0, тоді вільний член =6 ділимо на 2 і отримаємо, що другий корінь квадратного тричлена =6/2=3.
Обчислення дискримінанту і коренів не є доцільним в план затраченого часу в порівнянні з методом запропонованим вище, тому позбувайтеся особливості у границі за вказаним алгоритмом.
Записуємо розклад квадратного тричлена на множників та розписуємо границю
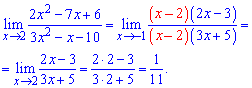
Як бачите, нічого складного в розкритті таких границь немає. Якщо задають частку многочленів вищого порядку за 2, то на момент вивчення границь Ви знаєте, як їх длити на одночлен, принаймі за програмою мали вже пройти. Серед завдань на невизначеність типу 0/0 зустрічаються такі, в яких потрібно застосовувати формули скороченого множення. Але якщо Ви їх не знаєте, то діленням многочлена на одночлен можна отримати потрібну формулу
Приклад 6. Знайти границю функції
Lim((x^2-9)/(x-3), x=3).
Розв'язання: Маємо невизначеність типу 0/0. В чисельнику застосовуємо формулу скороченого множення
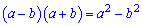
і обчислюємо потрібну границю
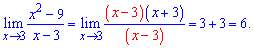
В результаті розкриємо невизначеність та отримаємо 6.
Метод розкриття невизначеності множенням на спряжене
Метод застосовують до границь, в яких невизначеність породжують ірраціональні функції. Чисельник або знаменник перетворюється в точці знаходження границі в нуль і невідомо як розкривати особливість 0/0.
Приклад 7. Знайти границю функції
Lim((sqrt(x+2)-sqrt(7x-10))/(3x-6), x=2).
Розв'язання: Подамо границю у вигляді формули
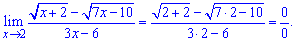
При підставленні значення x=2 отримаємо невизначеність типу 0/0.
Схема розкриття даної особливості полягає у множенні ірраціонального виразу, що її містить, на спряжене. Щоб вираз не змінився знаменник потрібно поділити на таке ж значення
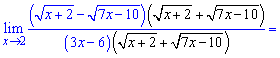
За правилом різниці квадратів перетворюємо чисельник та обчислюємо границю
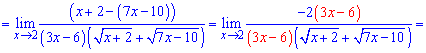
Спрощуємо доданки, що вносять особливість в границю та виконуємо підставлення
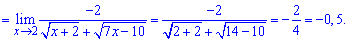
Вкінці залишиться обчислити корені квадратні в знаменнику та спротити дріб.
Приклад 8. Знайти границю функції
Lim((sqrt(x-2)-sqrt(2x-5))/(3-x), x=3).
Розв'язання: Границя має особливість виду 0/0.
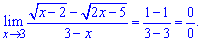
Для розкриття множимо і ділимо на спряжений вираз
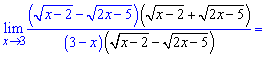
Записуємо різницю квадратів
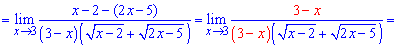
Спрощуємо доданки, що вносять особливість та знаходимо границю
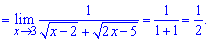
Достатньо простий прикад розкриття особливості методом позбуття ірраціональності.
Приклад 9. Знайти границю функції
Lim((x^2+x-6)/(sqrt(3x-2)-2), x=2).
Розв'язання: Підставимо двійку в границю.
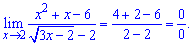
Отримаємо невизначеність 0/0.
Знаменник потрібно домножити на спряжений вираз, а в чисельнику розкласти квадратний тричлен шляхом розв'язку відповідного квадратного рівняння. Оскільки відомо, що 2 є коренем, то другий корінь знаходимо за теоремою Вієта
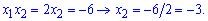
Таким чином чисельник запишемо у вигляді
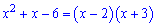
та підставимо у границю
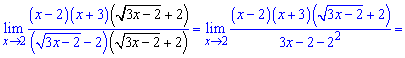
Звівши різницю квадратів позбуваємося особливості в чисельнику і знаменнику
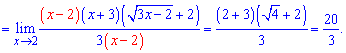
Наведеним чином можна позбутися особливості в багатьох прикладах, а застосування правила треба передбачатии всюди, де задають різницю коренів, що перетворюється в нуль при підстановці. Інші типи границь містять показникові функції, нескінченно малі функції, логарифми, особливі границі і т.д., та нові для Вас методики розкриття. Про це Ви зможете прочитати в наведених далі уроках на границі.
Обчислення границь в Мейплі
Даний матеріал корисний перш за все для студентів. Можливо в програмі навчання, а дехто для себе вивчає математичні програми та пакети, які дозволяють полегшити ручні розрахунки і перевірки розв'язків, автоматизувати обчислення.
Це можуть бути математичні пакети MathСad, Мathematica, Maple, MatLab.
Обчислення границь в Мейплі досить просто організувати навіть новачку.
Все, що потрібно - правильно ввести функцію, границю якої знаходимо.
> restart;
Границя першої функції в Мейпл матиме наступний запис.
Тиснемо вкінці набраного коду "Enter" і отримаємо кінцеве значення границі
> limit((x^2+3*x)/(2*x+5),x=3); 18/11
Границю другої функції отримаємо із запису
> limit((x^2+2*x)/(4*x^2+3*x-4),x=infinity); 1/4
Третій приклад прийме наступний вигляд:
> limit((x^2+3*x-5)/(x^2+x+2),x=infinity); 1
Мейпл без проблем знаходить першу чудову границю
> limit(sin(x)/x,x=0); 1
та другу чудову границю
> limit((1+1/x)^x,x=infinity); exp(1).
Фрагмент обчислення границь в математичному пакеті Мейпл наведено нижче
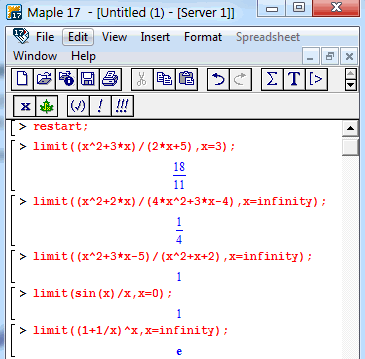В наступних публікаціях проаналізовано готові відповіді до понад 200 прикладів на границі.
Матеріал в повній мірі відповідає вимогам ВУЗ-ів та доможе вивчити тему самому лінивому студенту.
Головне - не спішіть, а уважно перечитуйте все що написано.
Решта перетворень містять формули, які розписані до дрібниць.
Переглянути схожі матеріали
]]>Основна суть в знаходженні таких границь полягає у виділенні із чисельника та знаменника найбільшого доданка чи множника. Після цього чисельник і знаменник ділять на це значення та отримують кінцевий результат.
Розглянемо задачі із збірника задач Дубовика В.П., Юрика І.І. "Вища математика".
Приклад 1. Знайти границі.
1) (4. 285)
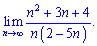
Розв'язок. В чисельнику і знаменнику виділяємо множник, який вносить найбільший вклад та скорочуємо на нього
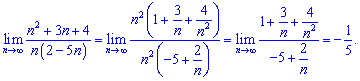
Д альше в дужках чисельника і знаменника бачимо домінуючі доданки, які і складають границю числової послідовності.
2) (4. 291)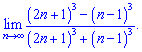 
Розв'язок. Виділяємо множники, що містять третю степінь і скорочуємо на них
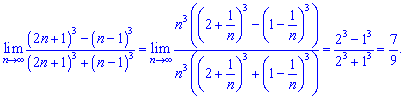
В підсумку записуємо ті додани, що внесуть вклад в границю послідовності.
3) (4. 293)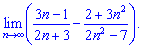 
Розв'язок. Розбиваємо даний приклад на суму двох границь, за правилами маємо право на це. Далі в кожній з границь виносимо в чисельнику та знаменнику домінючі множники за дужки
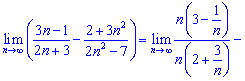
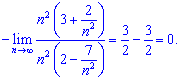
В результаті прийдемо до того, що границі рівні, оже їхня різниця - нуль.
4) (4. 295)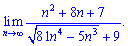 
Розв'язок. В такого типу прикладах потрібно винести в знамениику з під кореня множник в найбільшому степені. Як це зробити - перемножити показники 4*(1/2)=2
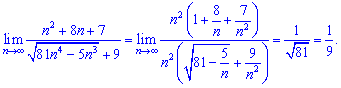
Далі приходимо до частки, яка в підсумку дає limit=1/9.
5) (4. 298)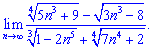 
Розв'язок. В цьому завданні та подібних потрібно знайти доданок з максимальним степенем
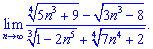
В чисельнику змінна n знаходиться в степенях 3/4 та 1/3. Змінна в знаменика є в степенях 5/3 та 1. Оскільки найбільший степінь знаменника 5/3 є більшим від степені чисельника 3/4, то знаменник зростатиме швидше ніж чисельник. В такому випадку границя послідовності рівна нулю
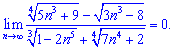
Якщо б було навпаки, то границя була б рівна нескінченності (
). У випадку однакових показників змінної, чисельник і знаменник скорочуємо на неї та отримуємо константу.
6)(4. 301)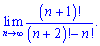 
Розв'язок. Границі з факторіалами займають особливе місце серед числових послідовностей. При їх знаходженні чисельник і знаменник розкладають до найбільшого спільного факторіалу
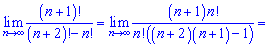
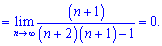
Даі спрощують спільні множники та аналізують швидкості зростання чи спадання послідовності. Границя рівна нулю, тому що степінь знаменника (2) більший від чисельника (1).
7) (4. 302)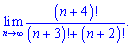 
Розв'язок. Як і у попередньому прикладі розкладаємо до найбільшого спільного факторіалу
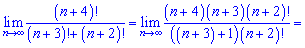
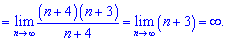
Тут картина протилежна - чисельник зростає квадратично, знаменник лінійно, тому границя послідовності прямує до безмежності.
8) (4. 304)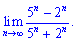 
Розв'язок. До прикладів, в яких змінна n виступає в ролі показника треба ставитися з особливою увагою. Незнання закономірностей поведінки степеневих функцій часто приводить до помилок в розв'язуванні. В даному прикладі 5n зростає значно швидше за 2n , тому його виділяємо як найбільший множник
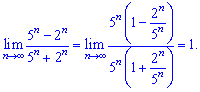
Далі бачимо, що двійа ніякого вкладу не вносить, а гриниця такої послідовності рівна одиниці.
9) (4. 307)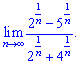 
Розв'язок.Числа в показникахі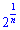
та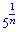 
прямують до одиниці (показники до нуля) при великих значеннях номера 
. На основі цього записуємо границю послідовності
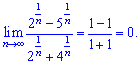
Подібних прикладів можна знайти чимало і розв'язування більшості з них полягає у знаходженні домінуючого множника. Якщо він у чисельнику то границя прямує до безмежності, у знаменнику – до нуля. І тільки коли найбільший множник присутній і там і там можна скоротити на цей множник дріб і отримати границю у вигляді константи. При факторіалах, числах в показниках схема виділення границі взагалі міняється, такі границі будуть детальніше розгляуті в наступних уроках.
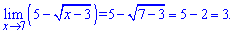
Розв'язання просте і зрозуміле кожному.
Труднощі виникають, якщо маємо наступні приклади функцій з коренями.
Приклад 1. Обчислити границю функції.
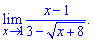
При прямій підстановці точки x=1 бачимо, що і чисельник і знаменник функції
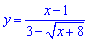
перетворюються в нуль, тобто маємо невизначеність 0/0.
Для розкриття такої невизначеності слід помножити вираз, що містить корінь на спряжений до нього та застосувати правило різниці квадратів. Для заданого прикладу перетворення будуть наступними
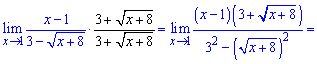
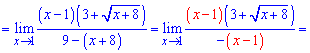
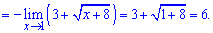
Границя функції рівна 6. Без наведеного правила її важко було б знайти.
Розглянемо подібні приклади обчислення границі на дане правило.
Приклад 2. Обчислити границю функції
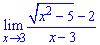
При підстановці x=3 отримаємо невизначеність виду 0/0.
Її розкриваємо множенням чисельника і знаменника на спряжене до чисельника.
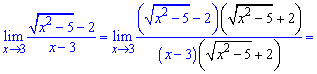
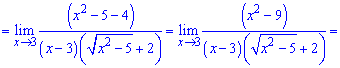
Чисельник розкладаємо за правилом різниці квадратів
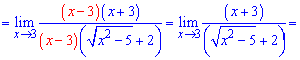
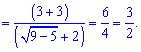
Ось так просто знайшли границю функції.
Приклад 3. Знайти границю функції
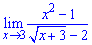
Бачимо, що маємо невизначеність виду 0/0.
Позбуваємося кореня в знаменнику
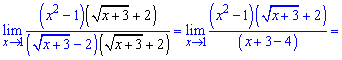
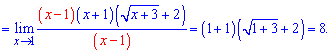
Границя функції рівна 8.
Тепер розглянемо інший тип прикладів, коли змінна прямує до безмежності.
Приклад 4. Обчислити границю
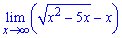
Маємо границю типу безмежність мінус безмежність. Множимо і ділимо на спряжений множник та використовуємо правило різниці квадратів
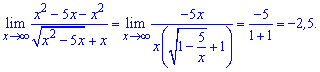
Границя функції рівна -2,5.
Приклад 5. Знайти границю функції
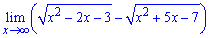
Границя еквівалента безмежність мінус безмежність
.
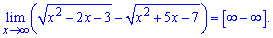Помножимо і поділимо на спряжене та виконаємо спрощення
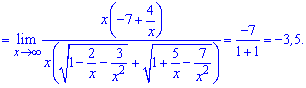
Винісши змінну в чисельнику та знаменнику можемо здогадатися до чого прямує функція.
Приклад 6. Чому рівна границя функції?
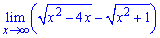
Маємо невизначеність виду безмежність мінус безмежність
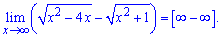
Виконуємо перетворення з кореневими функціями
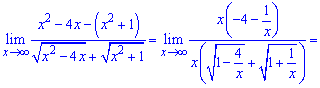
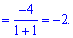
Границя рівна -2.
Добре перегляньте методику розкриття невизначеностей, алгоритм досить простий і допоможемо знайти складну границю.
Переглянути подібні матеріали
]]>Справа полягає в тім, що є багато правил та прийомів, які дозволяють по вигляду заданої функції чи послідовності швидко зорієнтуватися як знаходити границю. Проте, при вивченні теоретичного матеріалу чи на практиних, Вам або на цьому не наголошують, або Ваші думки гуляють за межами аудиторії.
Для охоплення всього матеріалу ми зібрали багато прикладів із студентської практики, модулів, контрольних, замовлень і спробуємо тут роз'яснити, як і в яких випадках методики застосовувати.
Приклад 1. Обчислити границю послідовності:
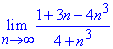
Розв'язання: При підстановці безмежності отримаємо невизначеність типу безмежність розділити на безмежність. Розділимо чисельник і знаменник на змінну в найбільшій степені і скоротимо на неї чисельник і знаменник. В результаті позбудемося невизначеності, а доданки що залишаться будуть прямувати до нуля при великих номерах послідовності
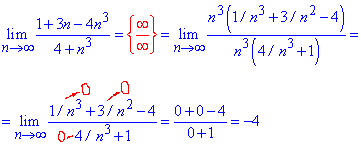
Всі сталі, що залишаться і вкажуть куди прямує границя.
Приклад 2. Обчислити границю послідовності:
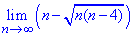
Розв'язання: При прямій підтановці нескінченно великого номера матимемо невизначеність безмежність мінус безмежність.
Правило розкриття такого типу невизначеності добре розписане в літературі і полягає в домноженні і розділенні невизначеності на множник спряжений до неї.
Як правило такі приклади містять корені і щоб їх позбутися використовуємо множення на спряжений множник, що призводить до різниці квадратів або кубів, в той час в знаменнику (або чисельнику) отримаємо вираз з коренем, що не містить невизначеності.
Далі з чисельника і знаменника виділяємо домінуючий множник та спрощуємо на нього.
Всі сталі, що залишаться і складуть границя послідовності.
Мовою формул це матиме запис
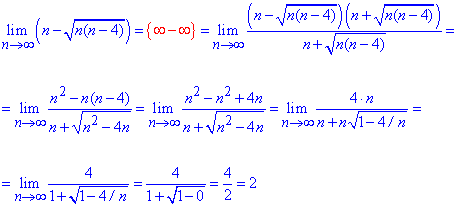
Приклад 3. Знайти границю функції:
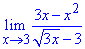
Розв'язання: При підстановці x=3 отримаємо невизначеність 0/0.
Це означає, що і чисельник і знаменник містять особливість.
Для розкриття невизначеності виділимо у чисельнику (x-3), а знаменник домножимо та розділимо на спряжений вираз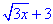 
.
В результаті отримаємо множник (x-3), на який спрощуємо дріб. Далі границя обчислюється методом підстановки змінної
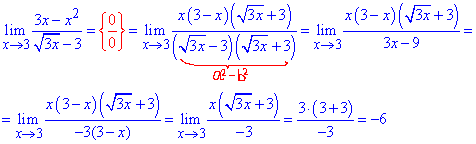
Приклад 4. Знайти границю функції:
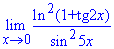
Розв'язання: Завдання для більшості студентів надзвичайно складне, а все тому що маємо звести невизначеність типу 0/0 до відомих випадків.
В результаті перетворення функцій отримаємо вирази виду ln(1+x)/x, tan(x)/x, sin(x)/x при змінній прямуючій до нуля.
Далі виділяємо першу важливу границю та її наслідки і розписуємо через добуток відомих границь.
Все решта зводиться до добутку одиниць та окремого множника, який і є границею заданої функції.
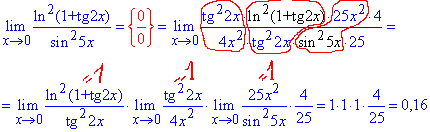
Уважно розберіть наведений приклад, він багато Вас навчить.
На практиці доволі важко знайти умову, яка б поєднувала декілька формул, тому вчіться на складних прикладах.
Тоді точно не матимете складнощів в обчисленні простих завдань.
Приклад 5. Обчислити границю функції:
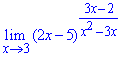
Розв'язання: Підстановка 3 в функцію дає особливість типу одиниця в степені безмежність. Для її розкриття і в функції в дужках і в дробі, що є показником виділяємо частину, що вносить особливість (х-3).
Далі для спрощення маніпуляцій з виразами робимо заміну змінних x-3=t, нова змінна при цьому прямує до нуля.
Після цього виділяємо другу чудову границю та шукаємо границю показника, що залишився.
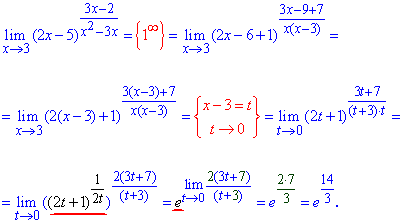
На цьому розбір поширених прикладів, які поширені в навчальній практиці не завершується.
В сусідній публікації будуть проаналізовані нові завдання, які допоможуть Вам швидше освоїти теоретичний матеріал та підготуватися до контрольної, модуля, екзамену.
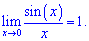
На її основі можна отримати ряд корисних для практики наслідків першої границі
1) 
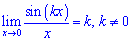
2) 
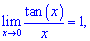
3) 
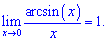
Друга особлива границя дозволяє розкривати невизначеності виду одиниця в степені безмежність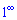 
.
Формула другої чудової границі наведена нижче
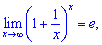
де e=2,71828182849045... – експонента.
На основі другої особливої границі отримують наступні формули (наслідки 2 границі)
1) 
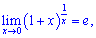
2) 
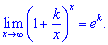
Завдання на границі, які зводяться до першої та другої особливих (чудових) границь зустрічаються доволі рідко, однак без наведених формул такі приклади не розв'язати. Розглянемо деякі приклади із збірника задач Дубовика В.П., Юрика І.І. "Вища математика", що приводять до застосування особливих границь.
Приклад 1. Знайти границю фунціїй.
1) (4. 388)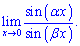 
Розв'язок. Помножимо чисельник і знаменник на аргумент та зведемо до першої чудової границі
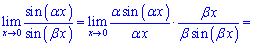
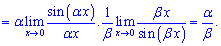
Для одних це легко побачити, іншим важко зрозуіти схему обчислень. А її суть в отриманні запису sin(x)/x, все що буде при цьому множником і буде складати границю функції.
2) (4. 393) 
Розв'язок. Поділимо чисельник і знаменник на змінну x. В результаті і там і там отримаємо "число" + наслідок перої особливої границі
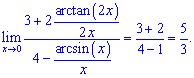
Настільки легко можна обчислювати, якщо мати шпаргалку та знати, що потрібно шукати.
3) (4. 399) 
Розв'язок.Згідно формули розвинення кореня в околі одиниці в ряд
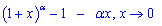
знаменник дробу можна перетворити наступним чином
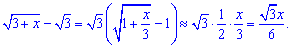
На основі цього знаходимо границю функції
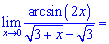
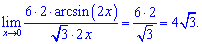
В чисельнику фігурував арксинус подвійного аргументу, тому для зведення під правило першої границі подвійний аргумент виділяємо також в знаменнику. Далі виписуємо границю у вигляді ірраціонального числа та, домноженням чисельника і знаменника на корінь з 3, приводимо запис до коректного вигляду.
4) (4. 432)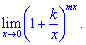 
Розв'язок.Зведемо показникову функцію під правило другої визначної границі. Для цього в степені утворємо множник обернено пропорційний до доданку в дужках.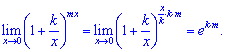
Все що залишиться і буде степенем експоненти. Застосовуйте цю властивість показників у подібних завданнях на границі.
5) (4. 437)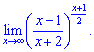 
Розв'язок. В такого роду завданнях функцію слід звести під формулу другої визначної границі.
Для цього зведемо до правильного дробу вираз в дужках
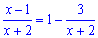
та підставимо в границю. Після розділення показників отримаємо добуток двох границь
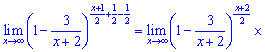
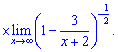
Спростимо перший множник
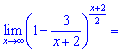
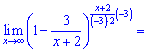
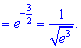
Друга границя рівна одиниці
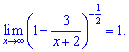
Просьба не вважати її чимось схожим на другу границю, в показнику немає аргументу "х", а вираз в дужках прямує до одиниці.
В результаті множення отримаємо
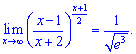
6) 
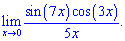
Розв'язок. Зведемо до першої визначної границі.
Тут зразу можна здогадатися, що косинус ніякого вкладу не внесе, оскільки в нулі рівний одиниці. Залишається в знаменнику отримати 7x
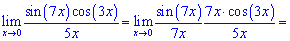
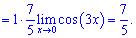
Після незначних перетворень границя функції рівна 7/5.
7) 
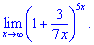
Розв'язок. Перетворимо показник для того, щоб можна було застосувати другу визначну границю.
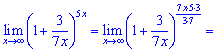
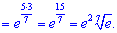
Перетворення дробу в показнику не складне і в результаті обчислень отримаємо e15/7.
Подібних прикладів можна навести сотні. Їх розв'язування дозволить закріпити Вам кращі практичні навички, тож пробуйте розв'язувати самостійно. Якщо в навчанні Вам зустрінуться важкі границі, порахувати які Ви не в змозі, звертайтеся до нас. Ми Вам в цьому допоможемо!
Переглянути подібні матеріали
]]>
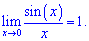
Наслідки першої особливої границі
Варто зазначити, що не всі границі, що містять тригонометричні функції слід зразу зводити до першої особливої границі. Все залежить, як входить функція, та чи можна звести під потрібну формулу. Плюс тригонометричні функції, коли ті прямують до нуля завжди можна замінити еквівалентними нескінченно малими виразами, але це вже інша техніка обчислення границь.
Слід відмітити, що на практиці в якості аргумента може виступати не тільки змінна, а й елементарна функція, поліном, чи будь-яка складна функція, що прямує до нуля. Про це Ви повинні пам'ятати і лише в таких випадках зводити обчислення під правило першої важливої границі. Важливо щоб змінна в тригонометричній функції прямувала до нуля, наприклад:
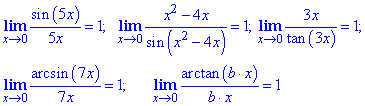
В наведених границях усі аргументи тригонометричних функцій прямують до нуля.
А от наступна границя знайдена неправильно
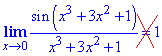
У Вас виникне запитання, Чому так? А тому що вираз x3+3x^2+1 не прямує до нуля, коли змінна x прямує до нуля.
Спробуйте самостійно знайти вказану границю, а ми вкінці статті звіримо відповіді.
Часто швидшим методом знаходження границі є заміна функцій еквівалентними (~) нескінченно малими величинами
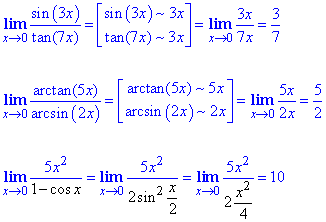
що є правильно, доцільно та виправдано в плані часу затраченого на розрахунки.
Але зараз в нас задача, навчити Вас розв'язувати завдання на першу границю, тому переходимо до підготовлених відповідей.
Приклади на першу важливу границю
Приклад 1 Знайти ліміт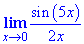 
Обчислення: Якщо бачите в границі синус, то з цього не завжди слідує про необхідність зводити до першої важливої границі
Спершу підставимо 0 в вираз під знаком ліміта (робимо це в голові не записуючи в зошит, або можете записати яку особливість дістанемо):
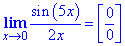
Отже, маємо особливість типу 0/0, її можна вказати при розв'язуванні, все залежить від ВУЗу та вимог оформлення границь. Дріб під знаком границі схожий на першу важливу границю, але це не вона.
Для зведення під формулу першої границі необхідно в штучний спосіб у знаменнику отримати такий самий вираз, який мститься під синусом.
На практиці виглядає це наступним чином:
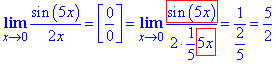
Обведений вираз в нас рівний першій границі, все решта множник при ній.
Аналогічно отримаєте якщо замінити синус еквівалентним нескінченно малим значенням sin(5x)~5x.
Відповідь: 5/2.
Приклад 2 Обчислити границю дробу
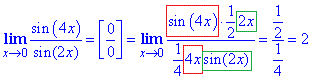
Обчислення: Чисельник та знаменник домножили на змінну, а далі штучно ввели множники які фігурують як аргументи синусів. Таким чином отримали дві чудові границі та сталі, які вкінці спростили.
Відповідь: 5/2.
Приклад 3 Знайти границю
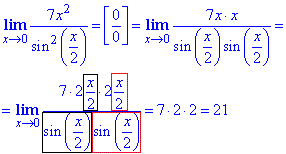
Обчислення: Тут штучно звели вираз в чисельнику під аргумент синуса в чисельнику та виразили першу визначну границю, після цього обчислення спростилися до множення трьох чисел.
Відповідь:21.
Приклад 4 Знайти границю
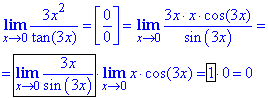
Обчислення: Проста підстановка показує, що маємо невизначеність виду 0/0, яку потрібно розкрити. Розпишемо в знаменнику tan(3x) за тригонометричною формулою tan(3x)=sin(3x)/cos(3x), а в чисельнику виділимо множник 3x. Таким чином отримаємо першу важливу границю помножену на границю від x•cos(3x), яка рівна нулю.
Тут не прийшлось шукати додаткові множники, проте розкриття невизначеності показало, що можна отримати в результаті як нуль, так і безмежність, якщо б мали обернений вираз.
Відповідь:0.
Приклад 5 Обчислити границю
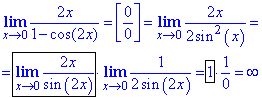
Обчислення: Невизначеність типу 0/0 розкриваємо шляхом виділення першої важливої границі, тільки цього разу вираз, що залишається в другій границі прямує до безмежності при змінній прямуючій до нуля.
Тут використали тригонометричну формулу
1-cos(2x)=2sin2(x).
Відповідь: ∞.
Бувають приклади коли застосування еквівалентних нескінченно малих величин є ефективнішим в плані простоти обчислень, ніж зведення під першу важливу границю.
Приклад 6 Знайти границю
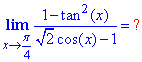
Обчислення: Легко переконатися, що чисельник і знаменник прямують до нуля. Для знаходження границі використаємо розклади функцй cos(x), tan2(x) по степенях при x→π/4.
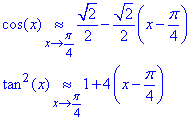
Підставимо отримані значення в границю
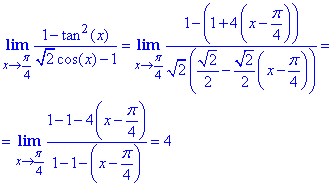
Відповідь:4.
Приклад 7 Знайти границю
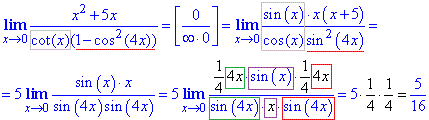
Обчислення: Тут сot(x) розписали за формулою ctg(x)=cos(x)/sin(x). Далі спростили доданки, які не вносять вкладу в границю. І наостанок в чисельнику та знаменнику ввели множники, які дозволили в одному прикладі виділити три перші особливі границі. Всі решта сталі псля множення дали значення границі.
Відповідь: 5/16.
Приклад 8 Знайти границю
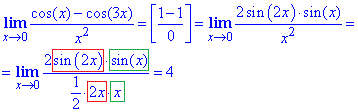
Обчислення: Отримали дещо іншу невизначеність від розглянутих раніше, яку розкрили за допомогою тригонометричної формули
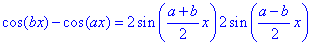
В результаті отримали добуток двох перших особливих границь.
Відповідь: 4.
Приклад 9 Обчислити границю
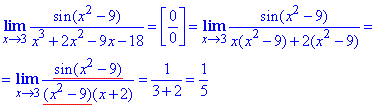
Обчислення: Розкрити невизначеність типу 0/0 вдалось завдяки виділенню в знаменнику множника ,який фігурує як аргумент синуса в чисельнику дробу. Тут можна було виконати заміну змінних y=x-3, що ви можете перевірити самостійно і подібним чином звести розв'язування до першої важливої границі.
Відповідь: 1/5.
Приклад 10Обчислити границю
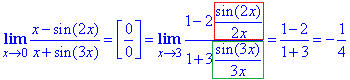
Обчислення:Підстановка 0 показує, що маємо невизначеність 0/0, яку необхідно розкрити. Щоб звести дріб під першу особливу границю в чисельнику та знаменнику виносимо аргумент та добиваємося, щоб дроби, що містить синуси мали в знаменнику однакові аргументи як у синусів.
Відповідь: -1/4.
Приклад 11 Обчислити границю
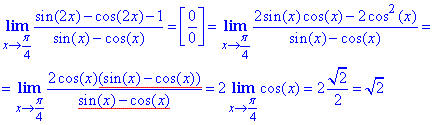
Тут використали тригонометричні формули синуса подвійного кута sin(2x)=2sin(x)cos(x) та залежність 1+cos(2x)=2cos2(x)
Відповідь: √2.
Приклад 12 Обчислити границю
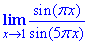
Розв'язування: Першу особливу границю тут застосовувати напряму неможна, оскільки аргументи πx, 5πx не прямують до нуля при x=1. Тому необхідно виконати заміну змінних x-1=y, тоді при x→1 змінна y→0, що й необхідно для застосування 1 особливої границі. Далі врахували періодичність тригонометричних функцій та штучно ввели потрібні множники
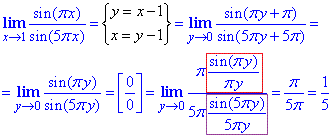
Відповідь: 1/5.
Приклад 13Обчислити границю
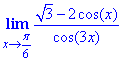
Розв'язування: Вводимо заміну змінних x-π/6=y, далі розписавши функції використовуємо тригонометричну форму представлення різниці косинусів через добуток відповідних синусів. Решта обчислень полягає в виділенні першої важливої границі
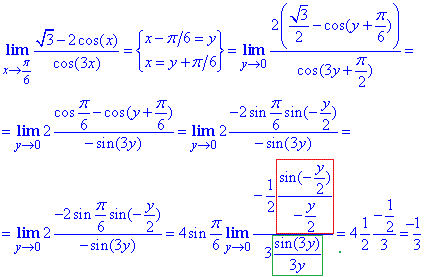
Відповідь: -1/3.
Приклад 14 Знайти ліміт функції
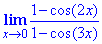
Розв'язування: Оскільки, взяті окремо границі чисельника 1-cos(2x) та знаменника 1-cos(3x) прямують до нуля коли x прямує до нуля, то маємо особливість типу нуль розділити на нуль. Розкриємо невизначеність за допомогою першої визначної границі. Для цього використаємо наступні тригонометричні формули, що, перейти від косинусів до синусів
1-cos(2x)=2sin2(x);
1-cos(3x)=2sin2(3x/2).
З врахуванням формул вище, обчислимо границю функції
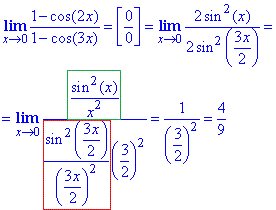
Відповідь: 4/9.
Приклад 15 Знайти ліміт функції
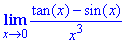
Розв'язування: Підстановка в уяві ургумента рівного нулю в чисельник і знаменник дає особливість типу нуль розділити на нуль 0/0. Щоб розкрити невизначеність розпишемо тангенс, а далі за тригонометричними формулами замінимо 1-cos(x)=2sin2(x/2). Далі штучним введенням потрібного множника зводима під правило першої визначної границі.
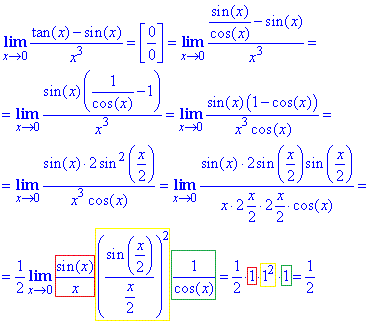
Відповідь:1/2.
При обчисленнях Вам часто доводиться використовувати різні тригонометричні формули, які дозволяють перейти до синусів. Ми для Вас їх згрупували, можете їх скопіювати, роздрукувати та використовувати в навчанні.
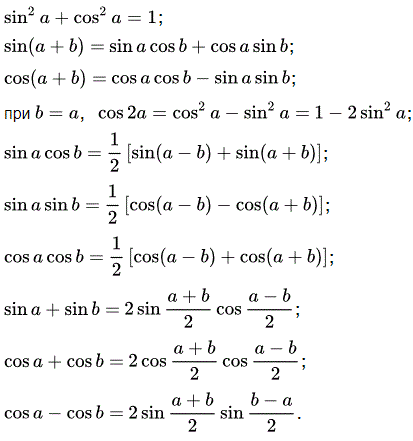
І на початку ми казали що границя 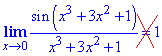подібна до першої, але не рівна 1, через те що аргумент не прямує до нуля. Якщо підставити нуль в чисельник та знаменник, то отримаємо limit=sin(1). Якщо Ви до цього прийшли самостійно, та можете розв'язувати наведені завдання без допомоги, то практикуми та екзамени здасьте на відмінно.
На цьогму розв'язування прикладів на першу важливу границю не закінчується, більше готових відповідей Ви можете знасти на сусідніх сторінках сайту.
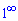. Формула другої чудової границі має наступний вигляд
сама границя рівна е – експоненті.
Наслідки другої особливої границі
Наведені формули є наслідками другої чудової границі (випливають з неї)
1) 
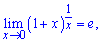
2) 
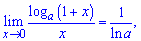
3) 
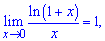
4) 
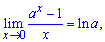
5) 
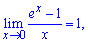
6) 
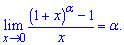
Наслідки рідше зустрічаються на практиці, проте без них деякі завдання в простий спосіб не розв'язати. Розглянемо деякі приклади із збірника А.В. Тевяшев, О.Г. Литвин, Г.М. Кривошеєва та ін. "Вища математика у прикладах та задачах. Ч.5 Тести"(Харків, 2007, Ст. 99).
Приклад 6.1.Знайти границю функції
а)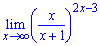 
Розв'язання.Перетворимо дробову функцію до вигляду, при якому можливо застосувати формулу чудової границі
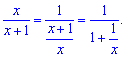
Вихідна границя прийме наступне значення
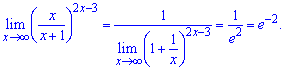
В результаті обчислень в показниу отримаємо двійку, а границя функції рівна e-2.
б)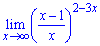 
Розв'язання. Подібно до попереднього прикладу розкладаємо дробову функцію у дужках
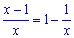
Потрібно зазначити, що в цьому прикладі та в багатьох подібних константи в степенях, як правило вкладу не несуть. Фунцію можна розписати через добуток двох
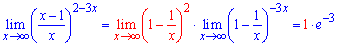
Границя навмисне розписана у вигляді добутку двох множників, щоб ви переконалися, що константи в степенях вкладу не дають (їх границя рівна одиниці). Їх мета запутати Вас, якщо погано знаєте теоретичний матеріал або сумніваєтеся в правильності розв'язання. В усіх наступних прикладах ми не будемо розписувати на добуток двох границь, проте пам'ятайте, що вони не змінюють кінцевого результату (вклад множник - одиниця).
в)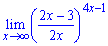 
Розв'язання. Виконуємо розлад функції у дужках
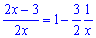
Запис в такому вигляді зроблено навмисне, тому що степінь потрібно звести до подібного вигляду (виразити обернено пропорційний множник)
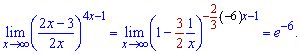
В такий простий спосіб отримали шукану границю функції. Надалі необхідні заміни або підказки будуть виділені кольором із загального розв'язання.
г)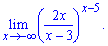 
Розв'язання. Виконаємо заміну змінних, щоб змінна прямувала до +безмежності, а не в протилежному напрямку
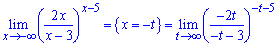
Даі перетворимо основу показникової залежності для знаходження границі
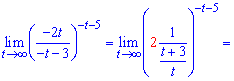
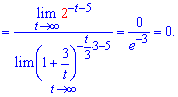
Бувають випадки коли прямо застосувати правило другої чудової границі доволі важко, в таких ситуаціях застосовуйте прості заміни, які Вам зрозумілі та дозволяють в швидкий спосіб знайти границю.
Приклад 6. 2Обчислити границю функції
а)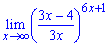 
Розв'язання.Виділяємо в дробовій функції одиницю та простий дріб
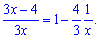
Підставляємо у границю та зводимо до експоненти, виконуючи неважкі маніпуляції зі степенями
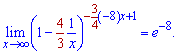
Отримали експоненту в -8 степені.
в)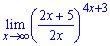 
Розв'язання. Зводимо дріб до найпростішого вигляду
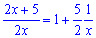
Застосовуючи означення другої важливої границі знайдемо
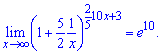
границю функції, яка рівна експоненті в 10 степені (e10).
Приклад 6. 3Знайти границю функції
б)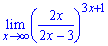 
Розв'язання. Перетворюємо дробову функцію
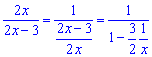
Підставляємо результати попередніх дій у границю та спрощуємо
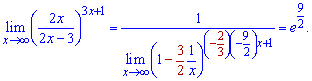
В результаті матимемо експоненту в степені e9/2.
г)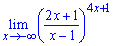 
Розв'язання. Аргумент прямує до мінус безмежності, крім того функція в дужках прямує не до одиниці, а до 2 при великих аргументах.
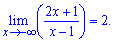
Таким чином маємо не другу особиву границю, а нескінченно спадну функцію - степінь від'ємний (змінна прямує до мінус безмежності).
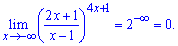
Звідси робимо висновок, що границя рівна нулю. Таке теж трапляється і будьте готові, що в завданні буде задана функція, яка за виглядом підходить правилу чудових границь, а по факту може бути як нескінченно зростаючою так і спадною функцією.
Приклад 6. 5Знайти границю
а)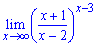 
Розв'язання. Заданий приклад на вигляд відрізняється від попередніх, проте розв'язок отримуємо за такою ж схемою. Виконуємо перетворення функції у дужках під правило
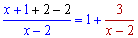
Залишилося в степені виділити обернений множник, для цього вионуємо наступні перетворення
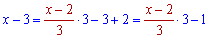
та підставляємо усе в формулу границі
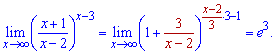
За такою схемою знаходьте усі подібні границі, вона проста та добре пояснює як звести завдання до особливих границь.
в)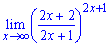 
Розв'язання. До розглянутого прикладу великих перетворень застосовувати не потрібно. Він має достатньо простий запис і обчислення границі виконуємо в один рядок
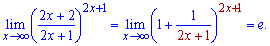
В усіх прикладах на другу визначну границю слід спочатку перевіряти, чи вираз в дужках прямує до одиниці. Якщо не прямує, то границя в залежності від степені буде рівна або нулю або нескінченності. Ті з Вас, хто часто розв'язує приклади, такі перевірки здійснює автоматично. Решта зводять границю до експоненти в певному степені, але все рівно вилазить множником або нуль або нескінченність. В кінцевому варіанті праві усі, проте у першому випадку витрачається набагато менше часу, який так необхідний на контрольних чи тестах. Тож вибирайте для себе простіший шлях та робіть в навчанні правильні висновки.
Практикуйте з подібними границями, використовуйте зручні для себе схеми зведення завдань під необхідне правило. Не бійтеся робити помилки, без них навчання не обходиться!
Переглянути подібні матеріали
]]>Випишемо формулу другої важливої границі та її наслідків
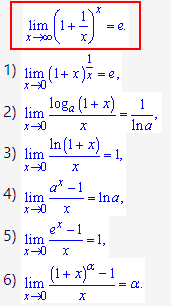(1)Як можна бачити, сама границя дозволяє розкрити невизначеності на нескінченності, її наслідки в нулі, коли зміннаи приймає безмежно малі значення.
Експонента e≈2,7182818284590452 Ви досить часто будете отримувати в математиці: зустрічається в границях, інтегралах, тригонометрії.
Розглянемо приклади та пояснимо алгоритм зведення невизначеностей під правило другої важливої границі.
Умову "Знайти границю" чи "Обчислити границю" в поясненнях опускаємо. Всі ми знаємо, що мета уроку навчитися бачити за формулою, які перетворення слід застосувати, щоб підвести описані вище невизначеності під формулу важливої границі.
Приклад 1. При підстановці отримаємо невизначеність типу одиниця в степені безмежність. Щоб її розкрити в чисельнику додаємо та віднімаємо одиницю, щоб отримати вираз як у знаменнику дробу, після чого ділимо. В результаті отримаємо в дужках одиниця мінус безмежно мала величина.
Щоб звести під правило 2 важливої границі в показнику потрібно виразити обрнену величину до другого доданку.
Для цього одночасно "ікс" множимо та ділимо на -1/(1+x).
Тоді перша частина дасть формулу 2 важливої границі, тому рівна експоненті, а границю степеня, що залишився обчислюємо
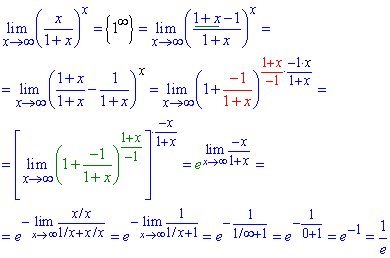
Не лякайтесь, що в формулі перед доданком стоїть знак "+", а в формулах "-".
Вся суть методу в тому, щоб отримати степінь обернений до доданку (зі знаком плюс чи мінус не важливо).
Приклад 2. Повторимо ті ж дії, щоб розкрити невизначеність виду {1∞}.
Наприкінці перетворень, щоб не залишати кореня квадратного в знаменнику перенесли його в чисельник.
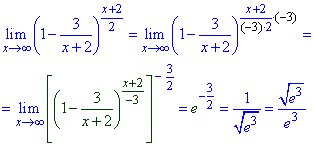
Приклад 3. Аназуючи доданок та степінь бачимо, що вони не є обернено пропорційні.
Тому спершу добиваємося, щоб вираз в дужках піднесений до степеня відповідав 2 важливій границі = експонеті, а границю степненя, що при цьому залишився розписуємо
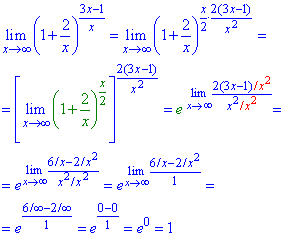
Приклад 4. Перше, на що слід звернути це те, що змінна не прямує ні до нуля, ні до нескінченності, а до одиниці.
Маємо невизначеність виду одиниця в степені нуль {1∞}.
Щоб її розкрити виділимо в дужках в штучний спосіб безмежно малу величину
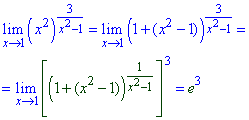
Тоді в степені виразимо обернену величину.
Отримаємо все, щоб застосувати наслідок другої чудової границі під номером 1) (вгорі).
Будьте готові до таких завдань та поступайте аналогічно.
Приклад 5. Перетворюємо чисельник, щоб отримати вираз рівний знаменнику.
Наступним кроком алгоритму є виділення в степені обернено пропорційного виразу до доданку в дужках.
Для цього "ікс", що є в степені, множимо та ділимор на доданок в дужках біля одиниці.
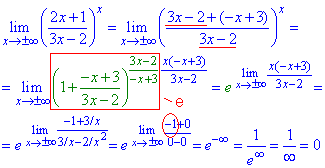
Подальші обчислення приводять до того, що в степені дістаємо дріб, знаменник якого безмежно малий.
В таких випадках будьте уважні, тому що в граничному переході отримаємо "+" або "-" нескінченність.
Все залежить від знаку чисельника!
Тому слідкуйте, який знак він приймає.
Приклад 6. Маємо частку квадратних тричленів, які в граничному переході дають особливість виду {1∞}.
Методика розкриття неодноразово тут наводилася - виділяємо в чисельнику квадратний тричлен, що є в знаменнику дробу.
Далі ділимо, щоб отримати вираз виду 1+ безмежно мала величина.
Обернену до неї записуємо множником в степінь, і в ньому ділимо на неї, щоб степінь залишився тим самим.
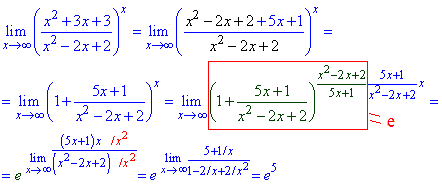
Отримуємо експоненту в степені =5, який визначаємо простим граничним переходом.
Всі деталі переходів містять формули, та й сам алгоритм зведення під правило другої важливої границі не важкий в застосуванні.
Приклад 7. Уважно перегляньте цей приклад. Під коренем Вам можуть задати будь-яку безмежно малу величину (синуси, тангенси, обернені функції, які прямують до нуля).
Вся робота зводиться до того, щоб виділити або доданок, або степінь обернений до доданку.
Тут звели до формули першого наслідку з другої чудової границі.
Крім того, в показнику отримали готову формулу першої важливої границі, а вона як Ви знаєте, рівна одиниці.
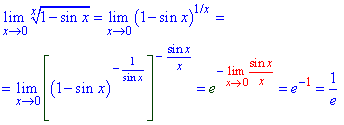
Ось такі бувають завдання одразу на дві важливі границі.
Приклад 7. Завдання подібне до попереднього, тільки тут потрібно не отримати експоненту.
А зауважити, що маємо не одиницю + безмежно малу величину, а 7.
Тому оцінюємо окремо вираз дужках, окремо степінь та знаходимо їх граничні значення:
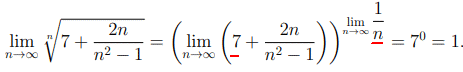
Думаю наступного разу Ви будете знати, як знайти границю, якщо вираз містить не одиницю.
Приклад 8. Зводимо під формулу другої важливої границі, попередньо націло поділивши дріб.
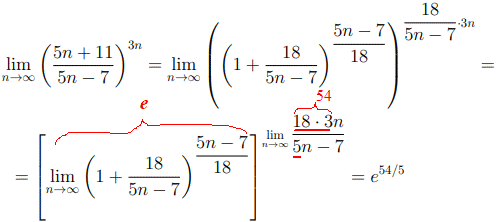
Приклад 9. Є і такий метод спрощення дробу – додати та відняти одиничку, а тоді одиницю зі знаком "-" звести з дробовою функцією до спільного знаменника. В результаті прийдемо до того, що в степені потрібно виразити обернений вираз, а все що залишиться оцінити.
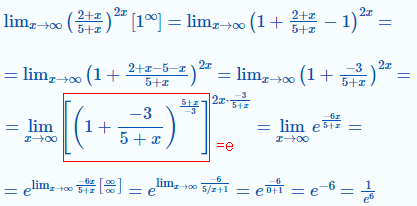
Для оцінки степенів пам'ятайте, що на безмежності найбільше впливає змінна в вищому степені,
в нулі – навпаки, чим менший степінь змінної, тим більше значення приймає вираз.
Побільше розв'язуйте самостійно, саме в цьому ключ до успіху в математиці!
]]>