Готові інтеграли функцій з контрольної роботи для студентів 1, 2 курсів математичних факультетів допоможуть вивчити не тільки схеми інтегрування, а й познайомлять з різноманітними прийомами, що полегшують знаходження інтегралів. Деякі завдання складні, і їх можуть зустріти в навчанні здебільшого математики, економісти, статисти, прикладники і фізики. Приклади завдань задавали на контрольній роботі в ЛНУ ім. І. Франка. Щоб формули в завданнях і відповідях не повторювалися самі завдання виписувати не будемо. Вам і так відомо, що в завданнях потрібно або "Знайти інтеграл" , або "Обчислити інтеграл".
Приклад 1. Перетворюємо корінь знаменнику на показник, далі виконуємо ділення і після цього інтегруємо згідно формул інтегрування степеневих функцій
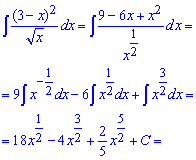
Після інтегрування відповідь переписуємо через корені
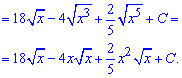
Приклад 2. Розбиваємо підінтегральну функцію на дві, першу з яких знаходимо за правилом інтегрування показникових функцій
![]()
Приклад 3. Перетворюємо підінтегральну функцію так, щоб під коренем при змінній коефіцієнт був рівний одиниці. За формулами інтегрування отримаємо арксинус
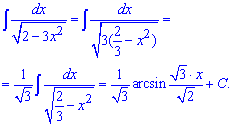
Заміна змінних під інтегралом
Приклад 4. Чисельник дробу перетворюємо таким чином, щоб він став рівним диференціалу від знаменника. Це дозволить застосувати заміну змінних та спростити інтегрування. В результаті отримаємо логарифм від функції, що знаходиться в знаменнику вихідного інтегралу
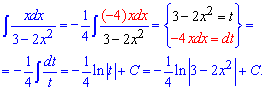
Приклад 5. В такого роду завданнях на інтеграли слід знати чому рівні похідні від тригонометричних функцій. В даному випадку, якщо за нову змінну вибрати котангенс та про диференціювати його то при підстановці отримаємо інтеграл від лінійної функції. Його знайти може учень 11 класу, проте не кожен учень зуміє побачити наведену заміну.
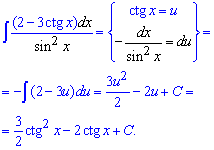
Після інтегрування всюди замість змінної підставляємо котангенс.
Приклад 6. Маємо дробову функцію, яка являє собою синус розділений на експоненту в степені косинус. Щоб перейти до другої основи інтегрування за змінну виберемо показник експоненти, продиференціюємо змінну та підставимо в інтеграл. При таких діях отримаємо інтеграл від експоненти з від'ємним показником. Його обчислюємо за табличною формулою
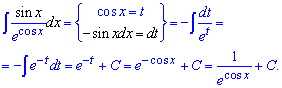
Приклад 7. Одиницю мінус логарифм позначимо за нову змінну, похідна нам дасть потрібну частину інтегралу. Після підстановки прийдемо до інтегрування степеневої функції з від'ємним показником.
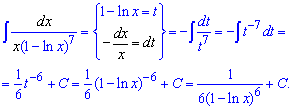
Вкінці не забувайте в усіх прикладах, де виконували заміну, підставляти початкову функцію (1-ln(x)).
Приклад 8. Декілька наступних завдань потрібно розв'язувати за правилом інтегрування частинами udv. За dv вибирають функцію, яка за 1 два роки приведе до рекурентної формули або після ряду повторного застосування правила інтегрування частинами отримаємо кінцеву відповідь. Тут косинус потрійного аргументу потрібно внести під диференціал
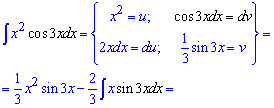
Повторно застосовуємо інтегрування частинами
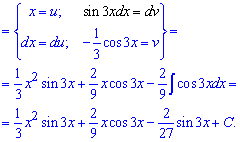
Як бачите нічого складного в інтегруванні немає, головне слідкувати за знаками синуса, косинуса.
Приклад 9. Завжди де бачите добуток експоненти на будь-яку функцію знайте, що доведеться інтегрувати частинами. Причому за dv вибираємо експоненту на dx.
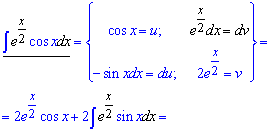
Після повторного інтегрування частинами отримаємо
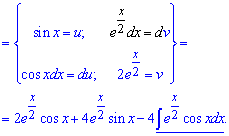
Слід зазначити, що далі інтегрувати ми не будемо. В такому отримали рекурентну формулу (справа і зліва від знаку рівності маємо потрібний інтеграл).
![]()
Переносимо невідомі по один знак рівності та обчислюємо інтеграл.
![]()
В подібних завданнях при інтегралі можуть бути не тільки константи, а й функції.
Приклад 10. Інтегруємо частинами, за функцію вибираємо арктангенс, за диференціал dv=x*dx. Після диференціювання арктангенса та інтегрування частинами другий інтеграл спроститься до двох табличних формул.
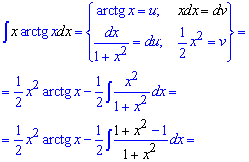
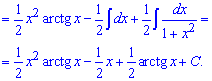
Приклад 11. Інтегруємо методом заміни змінних. Змінну вибираємо таким чином, щоб в показнику експоненти позбутися ірраціональності. Далі приходимо до інтегрування частинами та загнавши експоненту під диференціал експоненту застосовуємо формули udv
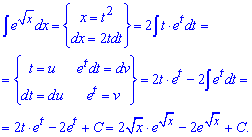
Приклад 12. В таких завданнях квадратний тричлен в знаменнику слід записати у вигляді різниці або суми квадратів. Далі прийдемо до інтегралу, що в підсумку дає арктангенс
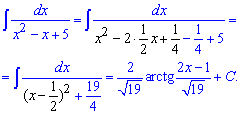
Приклад 13. Виділяємо квадрати під коренем та зводимо інтеграл до арксинуса.
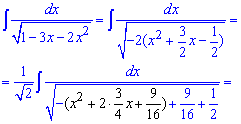
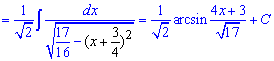
Ось і кінець уроку, в ньому при мінімальних поясненнях Ви отримали якісні схеми та поради для обчислення невизначених інтегралів. Користуйтеся ними та застосовуйте на практиці.
При групуванні уважно слідкуйте за сумою дробів, в такій простій операції левова частка помилок при інтегруванні, принаймні для тих хто дійшов хоч до якоїсь відповіді. Також запам'ятайте схему обчислень цього та попереднього прикладів, вони є поширеними на контрольних і тестах.
Готові розв'язки контрольної з інтегрування


