Об'єм тіла обертання навколо осі Ox, Oy

Об'єм тіла V, утвореного обертанням навколо осі Ox фігури 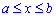, , 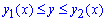де y₁(x) і y₂(x) - неперервні невід'ємні функції, дорівнює визначеному інтервалу від різниці квадрату функцій y_i(x) за змінною x

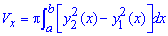
Об'єм тіла V, утвореного обертанням навколо осі Oy фігури 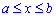, , 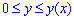де y(x) - однозначна неперервна функція, дорівнює визначеному інтегралу, розрахованому за формулою

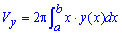
Приклади вибрано із навчальної програми для студентів механіко-математичного факультету Львівського національного університету імені Івана Франка. Решта ВУЗів України мають подібну програму навчання, завдання схожі, а в ряді випадків співпадають.
Наведені пояснення навчать Вас обчислювати типові завдання з наступних тем:

Приклад 1. Знайти об'єм тіла, що отримано обертанням ліній y=x³, y=8, x=0 навколо вісі Оx. Зробити малюнок.
Обчислення: Запишемо графіки функцій, що обмежують задану область:
y₁(x)=x^3, y₂(x)=8.
Знайдемо межі інтегрування, тобто точки абсцис перетину заданих функцій y₁(x)=y₂(x):
x^3=8 , x^3=2^3, x=2.
Запишемо межі інтегрування:
0≤x≤2.
x^3≤8 на [0;2], тому y₂(x)≥y₁(x).
Запам'ятайте, порядок функцій слід встановити, в іншому разі після інтегрування у Вас може вийти від'ємне значення і буде потрібно змінити місцями порядок функцій під інтегралом.
Побудуємо рисунок області, площу якої знаходимо інтегруванням

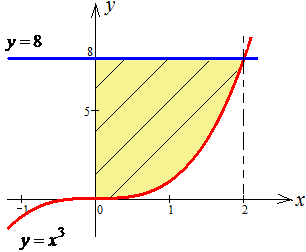
Знайдемо об'єм тіла обертання навколо осі Ox:

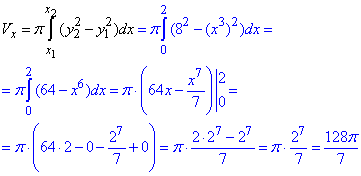
Об'єм рівний 128π/7 куб. од.

Далі в прикладах перший номер  відповідає номеру основного завдання зі збірника М. В. Заболоцький, Фединяк С.І., Філевич П.В. "Практикум з математичного аналізу" (поруч стоїть номер зі збірника Б. П. Демидовича).
Для вивчення основних моментів схема інтегрування та формули обчислення об'єму тіла обертання будуть повторюватися з прикладу в приклад.

ІV. Знайти об'єми тіл, обмеженими поверхнями, отриманими при обертанні відрізків наступних ліній

Приклад 2.139 (2472) Знайти об'єм тіла, утвореного обертанням кривої 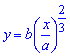(нейлоїд), xє[0;a] навколо осі Ox.
Розв'язання: Складаємо підінтегральну функцію:

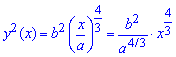
Межі інтегрування відомі за умовою: [0;a].
Знайдемо об'єм тіла інтегруванням:

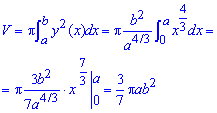
Пам'ятаємо, що об'єм вимірюється в кубічних одиницях.

Приклад 2.140 (2473) Знайти об'єм тіла, утвореного обертанням кривої 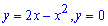а) навколо осі Ox; б) навколо осі Oy.
Розв'язання: Запишемо підінтегральні функції:
а)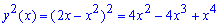
б)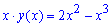
З наведених формул Ви можете бачити різницю, в яких випадках застосовувати кожну з формул об'єму.
Знайдемо межі інтегрування:

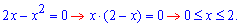
І заключним кроком обчислюємо об'єми інтегруванням.
а) Знайдемо об'єм тіла обертання навколо осі Ox:

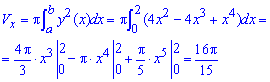
б) Обчислимо об'єм тіла обертання навколо осі Oy:

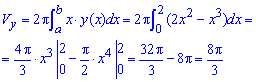
В даному прикладі інтеграли легко беруться і немає потреби пояснювати деталі операцій.

Приклад 2.141 (2474) Обчислити об'єм тіла, утвореного обертанням кривої 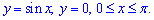а) навколо осі Ox; б) навколо осі Oy.
Розв'язання: Випишемо підінтегральні функції:
а)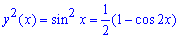
б)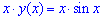
Межі інтегрування беремо із початкової умови: .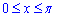
Залишилося обчислити визначені інтеграли:
а) Знайдемо об'єм тіла обертання навколо осі Ox:

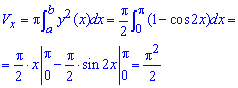
б) Виконуємо обчислення об'єму тіла при обертанні навколо осі Oy:

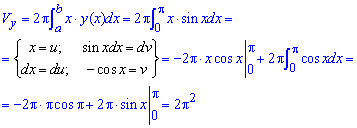
Заміна змінних допомагає знайти останній інтеграл.

Приклад 2.142 (2475) Знайти об'єм тіла, утвореного обертанням кривої 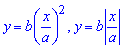а) навколо осі Ox; б) навколо осі Oy.
Розв'язання: Щоб записати підінтегральну функцію знайдемо різницю квадратів заданих функцій:
а)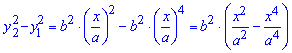
б) для тіла, утвореного обертанням навколо осі Oy підінтегральна функція має вигляд
;
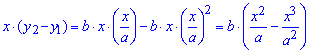З умови рівності функцій y₁(x)=y₂(x) визначаємо межі інтегрування

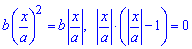
x₁=0, |x|=a, тому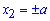
Межі інтегрування:
а) ;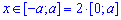
б) .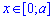
При : тому беручи до уваги симетрію маємо нерівність .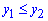
а) Обчислюємо об'єм тіла обертання навколо осі Ox:

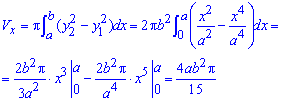
б) Через наступний інтеграл визначаємо об'єм тіла обертання навколо осі Oy:

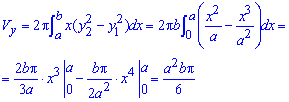
Тут теж немає що коментувати при обчисленні інтегралів.

Приклад 2.143 (2476) Знайти об'єм тіла, утвореного обертанням кривої y=e^-x, y=0, 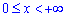а) навколо осі Ox; б) навколо осі Oy.
Розв'язання: Рівняння підінтегральних функцій:
а) y²=e^-2x;
б) x*y(x)=xe^-x.
Запишемо межі інтегрування (відомо за умовою): .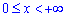
а) Знаходимо об'єм тіла обертання навколо осі Ox:

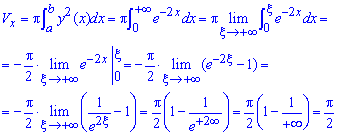
б) Знайдемо об'єм тіла обертання навколо осі Oy:


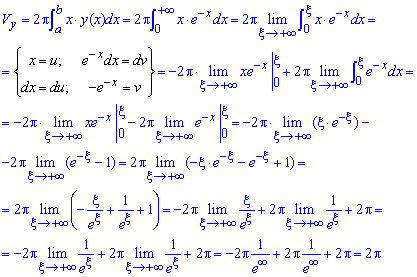
Тут щоб обчислити інтеграли доводиться знаходити границю при змінній прямуючій до безмежності. В другому інтегралі виконуємо інтегрування частинами.

Приклад 2.144 (2477) Обчислити об'єм тіла, утвореного обертанням кривої x²+(y-b)²=a², 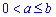, навколо осі Ox.
Розв'язання: Фігурою обертання є коло з центром в точці (0;b) і радіусом a.
При вираженні самої функції отримаємо дві вітки кореневих функцій:

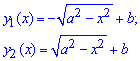
При піднесенні до квадрату різниця доданків складе такий вираз підінтегральної функції:

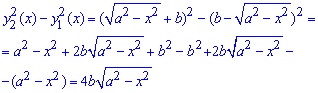
Запишемо межі інтегрування: для кола вони рівні xє[-a;a] або два півкола з на проміжку xє[0;a].
Через інтеграл знаходимо об'єм тіла обертання навколо осі Ox:

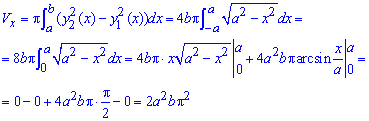
Уважно розберіть наведену відповідь.

Приклад 2.145 (2478) Знайти об'єм тіла, утвореного обертанням кривої x²-xy+y²=a², навколо осі Ox.
Розв'язання: Звівши криву до канонічного вигляду (методами з аналітичної геометрії) встановлюємо, що задана лінія є еліпсом
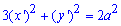- р-ня в канонічній системи координат.
У приведеній системі координат рівняння еліпса має вигляд:

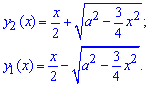
Пряма y=x/2 є віссю симетрії цієї фігури.
Запишемо підінтегральну функцію:
.
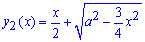Знайдемо межі інтегрування з умови y₂(x)=y₁(x):


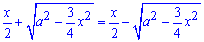
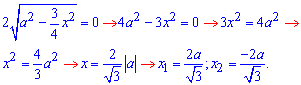
або двократний об'єм на інтервалі .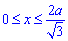
Але тоді ще потрібно відняти об'єм тіла в межах 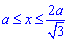(яка не належить еліпсу) і обмежена першою кривою

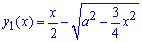
і результат помножити на 2 (симетрія).
Останнім кроком обчислюємо об'єм тіла обертання навколо осі Ox:

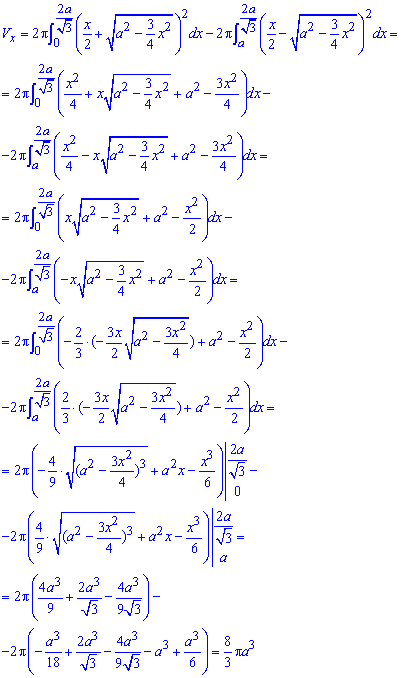
Інтеграл вийшов досить довгий, проте його зручно користувачам, які заходять на сайт з мобільних пристроїв.

Приклад 2.146 (2479) Знайти об'єм тіла, утвореного обертанням кривої 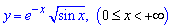навколо осі Ox.
Розв'язання: Запишемо підінтегральну функцію:
y²(x)=e^-2x*sin(x).
Встановимо межі інтегрування: 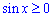при 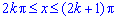, де k=0, 1,2,…
Таким чином маємо безмежний ряд проміжків інтегрування.
При знаходженні об'єму тіла обертання навколо осі Ox отримаємо безмежний ряд інтегралів, який є збіжним:

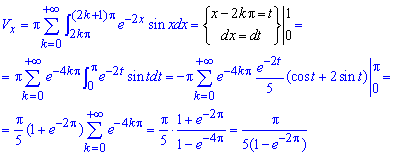
Тут обчислили інтеграл двічі виконавши заміну змінних:

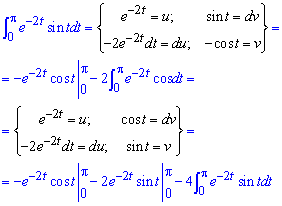
тому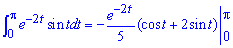
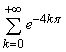- це числовий ряд.
В даному випадку нескінченно спадна геометрична прогресія, у якої b₁=1, b₂=e^-4Pi , тому q=e^-4Pi, а сума прогресії рівна

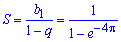
Приклад 2480 Знайти об'єм тіла, утвореного обертанням кривої x=a(t-sin(t)), y=a(1-cos(t)), 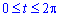, y=0. а) навколо осі Ox; б) навколо осі Oy; в) навколо прямої y=2a.
Розв'язання: Обчислимо підінтегральну функцію та диференціал по аргументу:
y²=a²(1-cos(t))², dx=a(1-cos(t))dt.
Межі інтегрування відомі з умови: tє[0;2Pi].
Переходимо до застосування формул об'ємів:
а) Першим обчислимо об'єм тіла обертання навколо осі Ox:

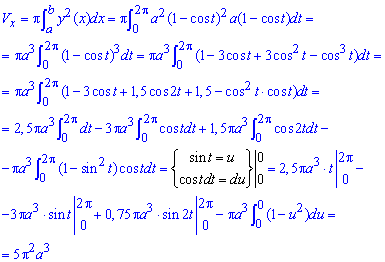
Тут застосована заміна змінних та умова ().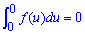

б) Наступним знайдемо об'єм тіла обертання навколо осі Oy:

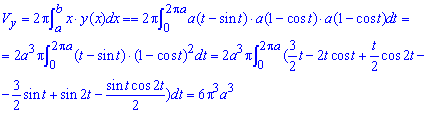
Його спробуйте розписати самостійно.

в) Останнім обчислимо об'єм тіла обертання навколо прямої y=2a:
Перейдемо до нової системи координат по формулам y₁=y-2a, x₁=x.
Тоді шуканий об'єм V=V₁-V₂, де V₁ - об'єм колового циліндра з висотою H=2Pi*a і радіусом основи R=2a, тому об'єм циліндра рівний
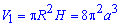куб. од.
Другий об'єм знаходимо інтегруванням

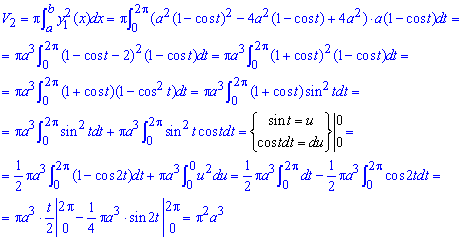
Як і у попередніх задачах тут використали заміну змінних під інтегралом.
Наостанок знаходимо різницю об'ємів
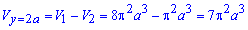куб. од.

Об'єм тіла, утвореного обертанням навколо полярної осі плоскої фігури

Щоб знайти об'єм тіла V, утвореного в результаті обертанням навколо полярної осі плоскої фігури r(phi)
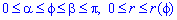необхідно обчислити визначений інтеграл за формулою

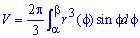
Приклад 2483 Знайти об'єм тіла, утвореного обертанням кривої r=a(1+cos(phi)), 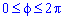, y=0
а) навколо полярної осі;
б) навколо прямої .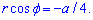
Розв'язання: Щоб дістати підінтегральну функцію підносимо до кубу задану функцію: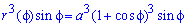
Межі інтегрування записуємо з початкової умови: .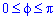
а) Спершу знайдемо об'єм тіла обертання навколо полярної осі:

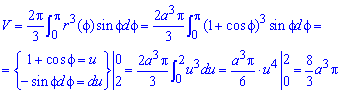
Для спрощення обчислень переходимо до нової змінної під інтегралом.
б) Перейдемо до нових координат за допомогою формул: x₁=y, y₁=-x-a/4.
Визначаємо межі інтегрування:
при зростанні кута 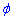від 0 до Pi/2 координата x₁ зростає від 0 до 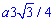, при зростанні 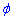від Pi/2 до Pi змінна x₁ спадає від 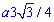до 0, тому межі обмежені інтервалом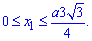
Запишемо підінтегральну функцію:
Рівняння переходу між системами координат мають вигляд

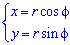
Підстановкою в рівняння отримаємо:
,
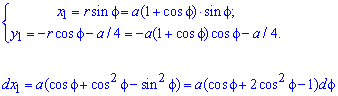Знайдемо об'єм тіла обертання навколо прямої :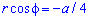

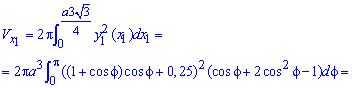
відкриємо дужки, зведемо подібні доданки і, врахувавши, що інтеграл рівний нулеві 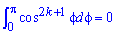отримаємо

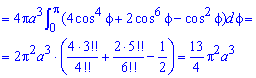
Тут останні інтеграли 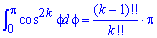виражаються через факторіали

(дивись приклад 2.59, частина І).
Парні факторіали обчислюємо за правилом

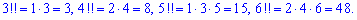
Приклад 2484.1 Знайти об'єм тіла, утвореного обертанням кривої r=a*phi, 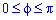(a>0), навколо полярної осі.
Розв'язання: Запишемо підінтегральну функцію: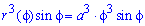
З межами інтегрування проблем немає: .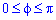
Щоб знайти об'єм тіла обертання навколо полярної осі виконуємо ряд маніпуляцій з інтегралами:

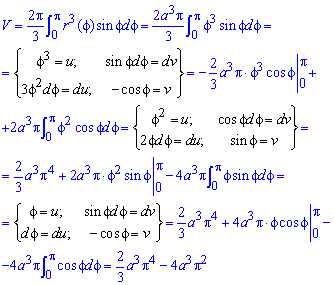
Уважно проаналізуйте, як знаходиться цей "тригонометричний" інтеграл.

Приклад 2484.2 Знайти об'єм тіла, утвореного обертанням кривої phi=Pi*r³, phi=Pi, навколо полярної осі.
Розв'язання: Запишемо підінтегральну функцію:

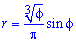
Межі інтегрування: .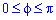
Обчислюємо об'єм тіла обертання навколо полярної осі:

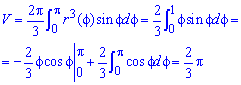
Тут синус вносимо під диференціал та виконуємо інтегрування частинами.
На даний час це всі приклади, які ми змогли підготувати для Вас з даної теми.