Обчислення подвійного інтеграла в полярних координатах

Детально проаналізуємо готові відповіді на обчислення подвійних інтегралів в полярній системі координат.
Уважно перечитайте як методику переходу від декартових до полярних координат, так і від чого змінюється складність знаходження подвійних інтегралів.

ЗАВДАННЯ 2.6 Обчислити подвійний інтеграл, використовуючи полярні координати:

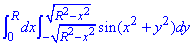
Розв'язання: Запишемо область інтегрування, що обмежена кривими
0≤x≤R,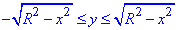
По осі "ігриків" маємо обмеження у вигляді двох віток півкола

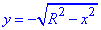
y²=R²-x², x²+y²=R².
Графік області інтегрування наведено на рисунку:

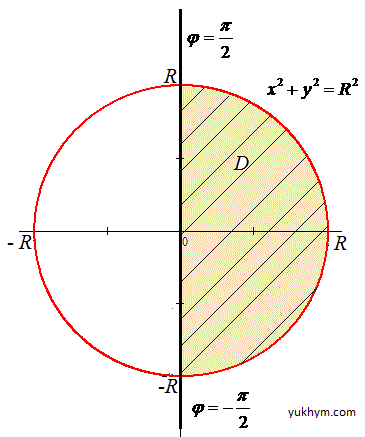
Отримали коло з центром у точці O(0;0) і радіусом R (нижня половина).
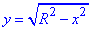- коло з центром у точці O(0;0) і радіусом R (верхня половина).
В усіх наступних прикладах не будемо повторювати наступні формули переходу від декартових до полярних координат:

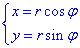
Якобіан всюди рівний I=r.
Знайдемо запис підінтегральної функції в полярній системі координат (ПСК):

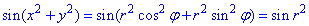
Запишемо, як поміняються межі при переході до нових координат:
0≤r≤R, -π/2≤φ≤π/2.
Далі розставляємо межі та знаходимо подвійний інтеграл:

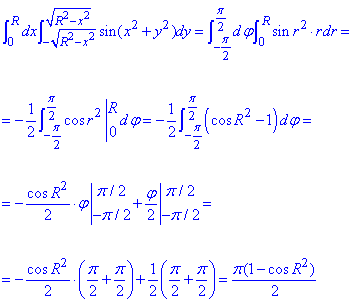
Уважно перегляньте, як виконується інтегрування. На вигляд все гладко, але так буває не зажди.
Все залежить від складності підінтегральних функцій та меж інтегрування.

ЗАВДАННЯ 2.7 Обчислити подвійний інтеграл, використовуючи полярні координати:

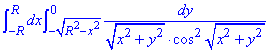
Розв'язання: Область інтегрування обмежена кривими
-R≤x≤R,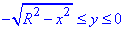
Одну з меж по "ігрик" зведемо до канонічного вигляду
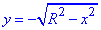, y²=R²-x², x²+y²=R².

Отримали коло з центром у точці O(0;0) і радіусом R (нижня половина). Побудуємо знайдену область.

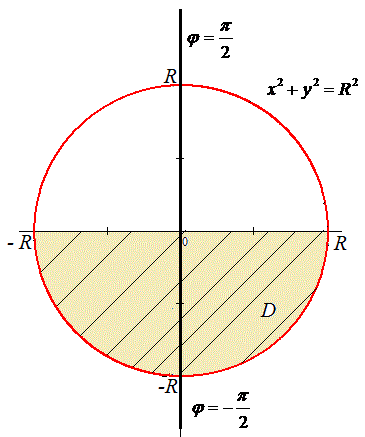
При переході до полярної системи координат якобіан рівний:
I=r.
Знайдемо вигляд підінтегральної функції в ПСК:

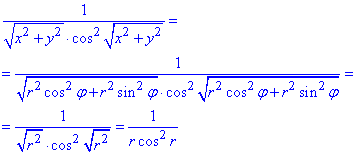
При спрощенні знаменника використана основна тригонометрична тотожність
cos²(a)+sin²(a)=1.
З графіка отримаємо наступні межі інтегрування:
0≤r≤R, π ≤φ≤2π.
Обчислимо подвійний інтеграл:

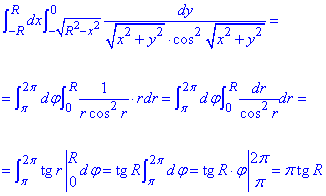
При інтегруванні отримали тангенс, далі підставили межі та виконали інтегрування за кутом.

ЗАВДАННЯ 2.8 Обчислити подвійний інтеграл, використовуючи полярні координати:

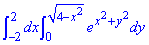
Розв'язання: Побудуємо область інтегрування, яка обмежена кривими
-2≤x≤2,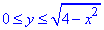
де y=√(4-x²), y²=4-x², x²+y²=2².
Отримали коло з центром у точці O(0;0) і радіусом 2 (верхня половина).

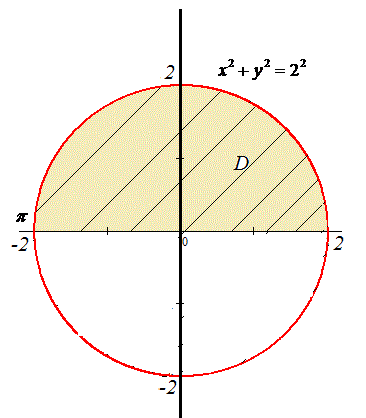
Перейдемо до полярної системи координат:
якобіан переходу: I=r.
Запишемо підінтегральну функцію в полярній системі координат:
.
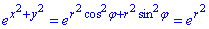Запишемо межі інтегрування в полярній системі координат:
0≤r≤2, 0≤φ≤π.
Обчислимо подвійний інтеграл:

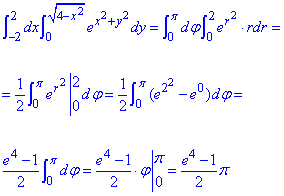
Розглянемо завдання де область інтегрування представлена кільцями.

ЗАВДАННЯ 2.9 Обчислити подвійний інтеграл, використовуючи полярні координати:

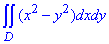
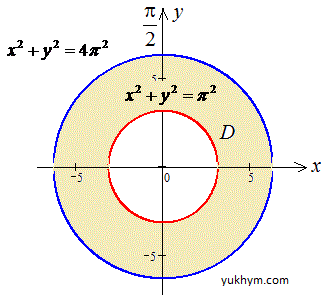
D:{x²+y²=π²; x²+y²=4π²}.
Розв'язання: Побудуємо область інтегрування, яка обмежена кривими
x²+y²=π² - отримали коло з центром у точці O(0;0) і радіусом π;
x²+y²=4π² - отримали коло з центром у точці O(0;0) і радіусом 2π.
Графічно вона має вигляд:

Якобіан переходу до полярної системи координат: I=r.
Запишемо підінтегральну функцію в полярній системі координат:

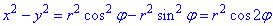
Знайдемо вигляд кривих в полярній системі координат:
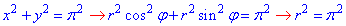, тобто r=π;
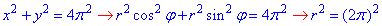,тобто r=2π.

Не важко переконатися, що межі інтегрування в полярній системі координат будуть наступними:
π≤r≤2π, 0≤φ≤2π.
Запам'ятайте, що сектори круга є найпростішими областями інтегрування.
Важче інтегрувати в ПСК параболи, гіперболи, еліпси та інші криві.
Знайдемо подвійний інтеграл:

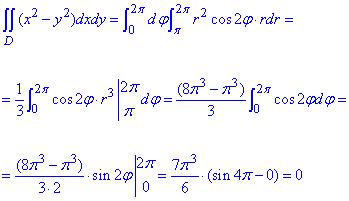
Інтеграл рівний нулю. Таких відповідей не лякайтеся, інтеграл це не площа, може приймати як нуль так і від'ємні значення.
Попереду Вас чекає безліч готових відповідей на різноманітні методи обчислення інтегралів.