Розглянемо готові відповіді до 35 тестових задач на прямі та площини в просторі. Умови завдань вимагають від Вас добрих знань стереометрії, ряду простих шкільних теорем та вміння схематично накреслити рисунки за умовами задач.
Розв'язки завдань будуть корисними в першу чергу учням 10-11 класів, та всім абітурієнтам, які готуються проходити тестування перед вступом у ВУЗи.
Пропонуємо завантажити відповіді (Посібник для підготовки до зовнішнього незалежного тестування з математики).
Автори: Анатолій Капіносов, Галина Білоусова, Галина Гап'юк, Сергій Мартинюк, Лариса Олійник, Петро Ульшин, Олег Чиж
Тема 35. Прямі та площини в просторі
Усі малюнки до задач виконані по новому з метою кращої їх візуалізації, та для того щоб Ви вчилися креслити якісні схематичні рисунки до умов завдань. Для простіших завдань добре виконаний рисунок може містити підказки, як шукати висоту, кут між прямими, чи доводити певну тотожність. Тому уважно аналізуйте пояснення до задач та використовуйте отримані знання на практиці.
Задача 35.1 Шість точок не лежать в одній площині. Яке найбільше число цих точок може лежати на одній прямій? 
Розв'язання: Нехай маємо шість точок A1, A2, …, A6 (N=6) і пряму a.
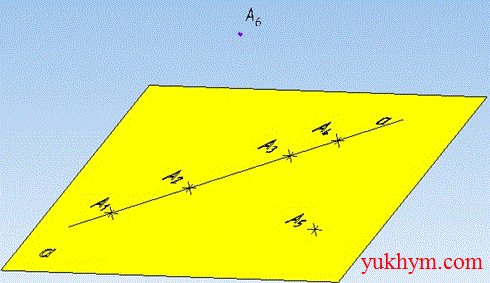
Відомо (за теоремою), що через пряму і точку, яка не лежить на цій прямій можна провести площину. Позначимо площину alpha, а точку, що не лежить на прямій A5 (точка 1).
За умовою задачі, шість точок не лежать в одній площині, означає, що хоча б одна не належить площині alpha. Нехай це буде точка A6 (точка 2).
Всі інші точки можуть лежати на одній прямій, тобто k=n-2=6-2=4, де k – кількість точок, що може лежати на одній прямій.
Відповідь: чотири – В.
Задача 35.2 На рисунку зображено тетраедр ABCD. Точка M належить ребру DB, а точка P – ребру DC.
Точки K1, K2, K3, K4 і K5 належать площині ABC.
У якій з цих точок пряма PM перетинає площину ABC? 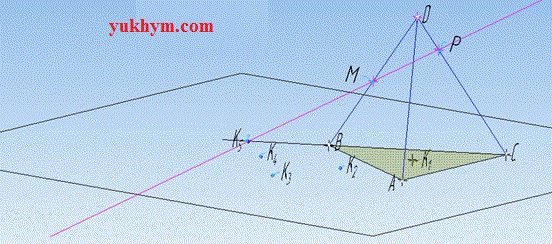
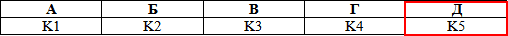
Розв'язання: Нехай маємо пряму PM. Ця пряма належить площині BCD, оскільки перетинає ребра DB і DC у точках M і P відповідно.
Оскільки задані точки K1, K2, K3, K4 і K5 належать площині ABC (за умовою задачі), то пряма PM перетне площину ABC по лінії перетину площин ABC і BCD, тобто по прямій BC.
Цій прямій належить точка K5, яка і буде точкою перетину прямої PM з площиною ABC.
Відповідь: K5 – Д.
Задача 35.3 На рисунку зображено куб ABCDA1B1C1D1 і точку M на ребрі BB1.
Якій із прямих належить точка перетину прямої MC із площиною A1B1C1?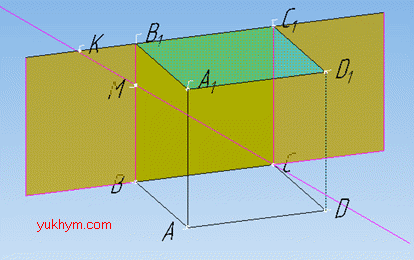
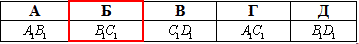
Розв'язання: Точки M і C належать площині BB1C1 (зелений колір), бо точка M належить ребру BB1 за умовою задачі.
За теоремою пряма MC також належить площині BB1C1.
Площини A1B1C1 і BB1C1 перетинаються по прямій B1C1.
Звідси випливає, що пряма MC перетинає площину A1B1C1 в точці (нехай це буде точка K), яка належить прямій B1C1 – прямій перетину площин A1B1C1 і BB1C1.
Відповідь: B1C1 – Б.
Задача 35.6 На рисунку площини alpha і beta перетинаються по прямій c.
Пряма a належить площині alpha, пряма b – площині beta.
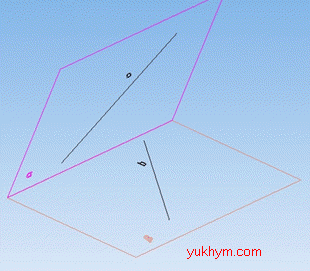
Яке з наведених тверджень правильне?

Розв'язання: Прямі a і b лежать в різних площинах і не мають спільної точки на прямій c – прямій перетину відповідних площин alpha і beta.
1) Тому прямі a і b не перетинаються (за теоремою).
Площини alpha і beta не є паралельними і прямі a і b не лежать в одній площині,
2) тому прямі a і b не є паралельними.
За означенням, прямі (в цій задачі a і b), які не перетинаються і не лежать в одній площині називаються мимобіжними.
Відповідь: прямі a і b мимобіжні – В.
Задача 35.23 На рисунку зображено піраміду SABCD, де SO – висота піраміди, M – середина висоти, K – середина ребра SA, P – середина ребра AB.
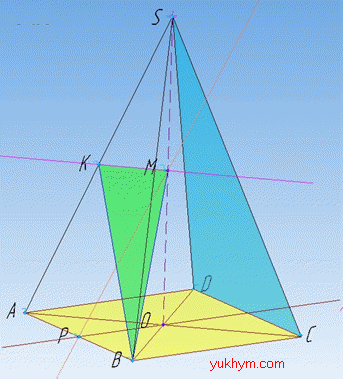
Установити відповідність між прямими і площинами (1–4) та їхнім взаємним розміщенням (А–Д).

Розв'язання: 1) Пряма AC належить площині ABC. Розглянемо трикутник ASC. Оскільки, за умовою, SO – висота піраміди, тому SO⊥(ABC), звідси слідує, що SO⊥AC (пряма, яка перпендикулярна до площини, перпендикулярна до кожної прямої, що належить цій площині).
Отже, SO – висота ΔASC. За умовою задачі M – середина висоти, K – середина ребра SA, звідси слідує, що пряма MK належить площині ASC, а відрізок MK є середньою лінією ΔASC (за означенням). Тому MK||AC (за властивістю середньої лінії трикутника), а отже, пряма MK паралельна площині ABC, тобто MK||(ABC), бо пряма, яка не належить площині паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. 1 – В.
2) Пряма OP належить площині ABC, оскільки точка O – основа висоти SO, що належить площині ABC;
точка P – середина ребра AB, що також належить площині ABC. Пряма MK не належить площині ABC, з нею не перетинається. Прямі OP і MK також не є паралельні (бо належать різним площинам), тому за означенням прямі OP і MK – мимобіжні (прямі в просторі, які лежать в різних площинах і не перетинаються називаються мимобіжними). 2 – Д.
3) Пряма MP проходить через точку M, яка є серединою висоти SO за умовою задачі. Висота SO і площина SDC перетинаються в точці S. Звідси слідує, що і пряма MO (яка є частиною прямої SO) перетинає площину SDC. Пряма MP належить площині MOP, в якій хоча б одна пряма (це MO) перетинає площину SDC. Звідси слідує, що кожна пряма, що належить площині MOP перетинає площину SDC, тобто пряма MP також перетинає площину SDC. 3 – Б.
4) В пункті 1) встановлено, що відрізок MK (що належить площині BMK) є середньою лінією ΔASC, тобто перетинає ребро SC (що належить площині SDC). Отже прямі MK і SC, що належать площинам BMK і SDC відповідно, перетинаються. Звідси слідує, що і самі площини BMK і SDC перетинаються. 4 – А.
Попереду на Вас чекає чимало готових відповідей до задач на прямі та площини в просторі. Всі вони сприятимуть Вашій підготовці з геометрії та допоможуть отримати високі бали при зовнішньому незалежному оцінюванні.
- Вас може зацікавити:
- Задачі на куб
- Правильна трикутна піраміда
- Задачі на паралелепіпед з відповідями



