Найпростіші задачі на знаходження радіуса кулі в умові мають задану або площу поверхні, або об'єм кулі. Для обчислення радіуса необхідно провести прості маніпуляції: виразити та добути корінь квадратний або кубічний. Такі приклади задають в 10-11 класах на уроках геометрії і їх тут повторно розжовувати немає змісту.
Розглянемо приклади на кулі, які перетинаються, вписані або описані навколо конуса, куба, піраміди.
В таких задачах також потрібно знайти радіус кулі, однак самі обчислення більш складні вимагають ряду обґрунтувань або виведення формул.
Наведені далі приклади підібрані з одного зі збірників для ЗНО підготовки за попередні роки.
Задача 40.12 Дві рівні кулі радіуса R розміщені так, що центр однієї з них лежить на поверхні іншої.
Знайти радіус кола, по якому перетинаються їхні поверхні.
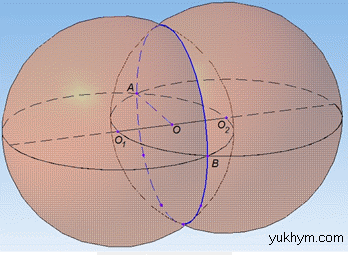
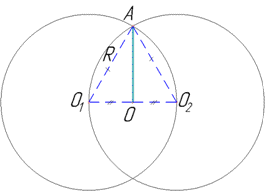
Розв'язання: Маємо дві рівні кулі радіуса R з центрами O1 і O2.
Ці дві кулі перетинаються по колу з центром O. Проведемо відрізок O1O2. Оскільки кулі рівні і центр однієї лежить на поверхні іншої (за умовою), то O1O2=R і O1O=O2O.
Позначимо точку A на лінії (на колі) перетину двох куль і проведемо відрізки O1A і O2A.
Оскільки точка A лежить на лінії перетину двох куль (за побудовою), то вона лежить на їх поверхні, звідси слідує, що O1A=R і O2A=R.
Отже, отримали O1O2=O1A=O2A=R, тобто трикутник AO1O2 – рівносторонній.
Оскільки центр O кола перетину двох рівних куль ділить відрізок O1O2 навпіл (цей факт потребує строге доведення), то відрізок AO – медіана, бісектриса і висота рівностороннього трикутника AO1O2 (OO1=OO2=R/2 та AO⊥O1O2), а також AO – радіус кола перетину двох куль, оскільки точка A лежить на колі перетину двох куль за побудовою. Отже, AO=√3R/2.
З прямокутного трикутника AOO1 (∠AOO1=90), в якому OO1=R/2 – катет і AO1=R – гіпотенуза, за теоремою Піфагора знайдемо катет AO – радіус кола:
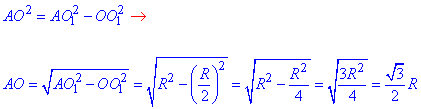
Отже, AO=√3R/2 – радіус перетину двох куль.
Відповідь: √3R/2 – В.
Задача 40.31 Навколо конуса з радіусом основи 9 і висотою 3 описано кулю.
Визначити радіус цієї кулі.
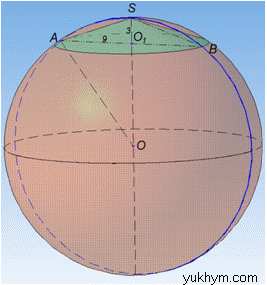
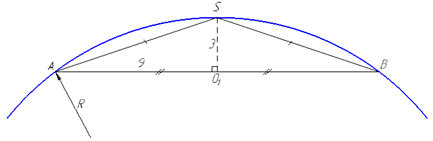
Розв'язання: Маємо кулю з центром O і вписаний в неї конус з висотою SO1=H=3 і радіусом основи AO1=BO1=R=9.
Куля описана навколо конуса:
1) якщо основа конуса співпадає з перерізом кулі, а вершина конуса належить кулі (за означенням);
2) якщо великий круг кулі описаний навколо осьового перерізу конуса (за властивістю).
Оскільки осьовий переріз конуса – рівнобедрений ΔSAB (детальніше про це дивись І абзац задачі 39.1), то достатньо знайти його радіус описаного круга R (це і буде радіус кулі).
Обчислимо бічні сторони рівнобедреного ΔSAB (твірну конуса) SA як гіпотенузу прямокутного ΔSAO1 (∠SO1A=90)
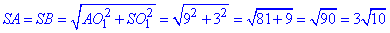
Площа осьового перерізу конуса, ΔSAB (тут AB=2AO1=2R=18):
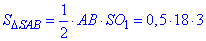
Знайдемо радіус великого круга (тобто радіус кулі) описаного навколо ΔSAB:
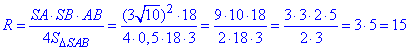
Отже, R=15 радіус описаної кулі навколо конуса.
Відповідь: 15.
Задача 40.32 У пряму чотирикутну призму, основою якої є ромб з діагоналями 3 і 4, вписано кулю.
Визначити радіус кулі.
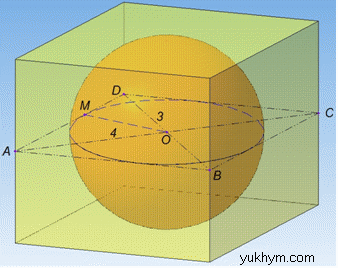
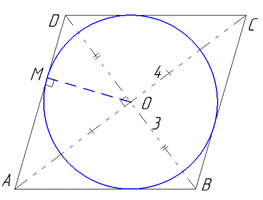
Розв'язання: Маємо пряму чотирикутну призму, основою якої є ромб з діагоналями 3 і 4, а також вписану в неї кулю з центром O.
Куля вписана у призму, якщо куля дотикається до всіх граней призми (за означенням).
Куля вписана у призму, якщо великий круг кулі є вписаним в ромб, який є одним і перерізів призми, проведених паралельно до її основи (за властивістю).
Нехай великий круг кулі з центром O вписаний у ромб ABCD, довжина діагоналей якого AC=4 і BD=3. В точці O діагоналі ромба перетинаються під прямим кутом і діляться навпіл:
AO=CO=2, DO=BO=1,5 і AO⊥DO.
Оскільки радіус вписаного круга r=MO в точці дотику перпендикулярний до сторони ромба AD⊥MO, то MO є висотою прямокутного трикутника AOD.
Із прямокутного ΔAOD (∠AOD=90) за теоремою Піфагора знайдемо гіпотенузу AD (сторону ромба ABCD):
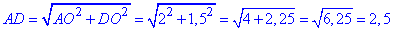
Із прямокутного ΔAOD (∠AOD=90) за означенням площі знайдемо висоту MO (радіус вписаного круга, тобто радіус кулі):
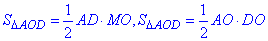– формули для обчислення площі трикутника ΔAOD, тоді
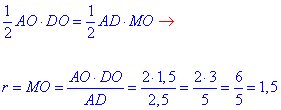
Отже, r=1,2 радіус вписаної кулі в пряму чотирикутну призму, основою якої є ромб.
Відповідь: 1,2.
Задача 40.33 У циліндр, об'єм якого дорівнює 16π, вписано кулю.
Знайти радіус кулі.
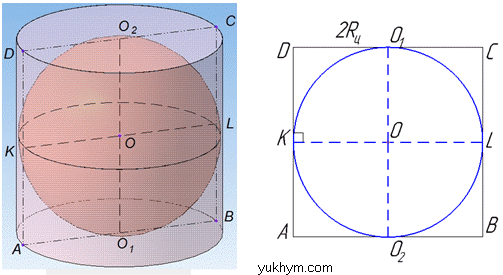
Розв'язання: Задача майже дублює задачу 40.18.
Об'єм циліндра обчислюють за формулою:
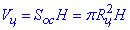
де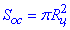 
– площа основи циліндра (площа круга);
H – висота циліндра.
Куля вписана у циліндр, якщо куля дотикається до основ і бічної поверхні циліндра (за означенням).
Куля вписана у циліндр, якщо її великий круг є вписаним в осьовий переріз циліндра (за властивістю).
Очевидно, що осьовим перерізом циліндра може бути квадрат, оскільки круг не може бути вписаний в прямокутник (який не є квадратом).
Оскільки осьовим перерізом циліндра є квадрат ABCD, то висота циліндра H дорівнює її діаметру D, або подвійному радіусу 2Rц, тобто H=2Rц.
Отже, об'єм циліндра:
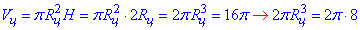
звідси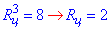 
– радіус циліндра. Оскільки великий круг кулі вписаний в осьовий переріз циліндра (квадрат ABCD), то за властивістю круга вписаного в квадрат:
діаметр круга KL дорівнює стороні квадрата AB, а значить подвійному радіусу циліндра:
Dк=2Rк=2Rц, звідси отримаємо Rк=Rц=2.
Rк=2 – кулі вписаної в циліндр з об'ємом 16π.
Відповідь: 2.
Задача 40.34 Висота конуса дорівнює 8 см, а його твірна дорівнює 10 см.
Знайти у сантиметрах радіус кулі, вписаної в конус.
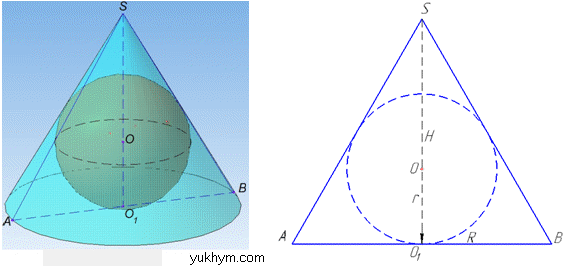
Розв'язання: Задача є аналогічною до 40.26, яка описана раніше.
Маємо кулю з центром O, яка вписана у конус з висотою H=SO1=8 см і твірною l=SA=SB=10 см.
Куля вписана у конус:
1) якщо вона дотикається до основи та бічної поверхні конуса (за означенням);
2) якщо великий круг кулі вписаний в осьовий переріз конуса (за властивістю).
Оскільки осьовий переріз конуса з центром основи O1 – рівнобедрений ΔSAB (дивись абзац І задачі 39.1), то висота конуса H=SO1=8 см є висотою ΔSAB, проведеного до основи AB=2R, а радіус кулі r є радіусом вписаного круга в рівнобедрений ΔSAB.
Радіус основи конуса R=AO1=BO1 знайдемо за допомогою теореми Піфагора у прямокутному SAO1 (∠SO1A=90), де SO1=8 см – катет і SA=10 см – гіпотенуза.
Отже,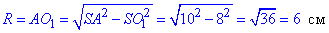 
Радіус вписаного в рівнобедрений трикутник ΔSAB круга знайдемо за формулою:
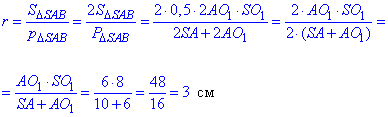
де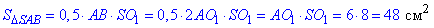 
– площа рівнобедреного ΔSAB;
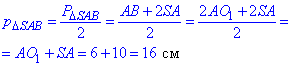– півпериметр рівнобедреного ΔSAB.
Отже, r=3 см – радіус кулі, вписаної в конус.
Відповідь: 3.
Задача 40.35 Основою піраміди є правильний трикутник зі стороною 6 см. Одне з бічних ребер піраміди є перпендикулярним до площини основи і дорівнює 4 см. Знайти у сантиметрах радіус кулі, описаної навколо піраміди.
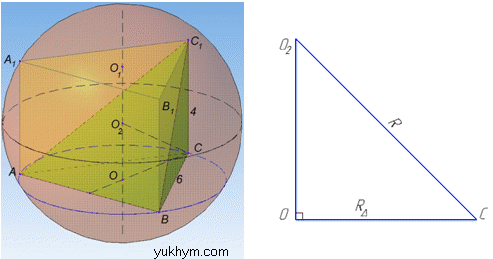
Розв'язання: Маємо кулю з центром O2 і вписану в неї піраміду C1ABC, в основі якої лежить правильний трикутник ABC зі стороною AB=BC=AC=a=6 см.
Нехай CC1=H=4 см – бічне ребро (висота) піраміди, оскільки CC1⊥(ABC), тому CC1 перпендикулярний до кожного відрізка, що належить ΔABC.
Оскільки основа піраміди – правильний ΔABC і CC1⊥(ABC), то до неї добудуємо піраміду з вершиною C1 і основою AA1B1B таким чином, щоб разом з попередньою пірамідою вони утворили правильну трикутну призму A1B1C1ABC, яка вписана в кулю.
Тоді за означенням правильної трикутної призми: основи – правильні рівні ΔABC і ΔA1B1C1, а висота цієї призми дорівнює висоті заданої піраміди:
AA1=BB1=CC1=H=4 см.
Оскільки правильна трикутна призма вписана в кулю (за побудовою), то основи ΔABC і ΔA1B1C1 вписані в круги з центрами O і O1 відповідно і розташовані на однаковій відстані від центра кулі, тобто OO2=O1O2 (за властивістю), але OO1=H=4 см – висота призми, тому OO2=O1O2=H/2=2 см.
У правильному ΔABC проведемо відрізок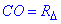 
– радіус описаного кола.
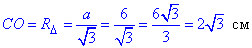
Оскільки OO1=H – висота призми та заданої піраміди, то OO1||CC1, а значить OO1⊥CO, тобто OO2⊥CO.
Проведемо відрізок CO2=R – радіус кулі.
Розглянемо прямокутний ΔCOO2 (∠COO2=90), у якому OO2=2 см і CO=2√3 см – катети.
За теоремою Піфагора знайдемо гіпотенузу CO2=R:
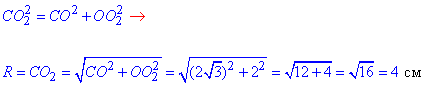
Отже, R=4 см – радіус кулі описаної навколо піраміди C1ABC.
Відповідь: 4.
Задача 40.36 Ребро правильного тетраедра дорівнює 3√6.
Визначити радіус сфери, яка дотикається до бічних граней тетраедра, якщо центр цієї сфери лежить на основі тетраедра.
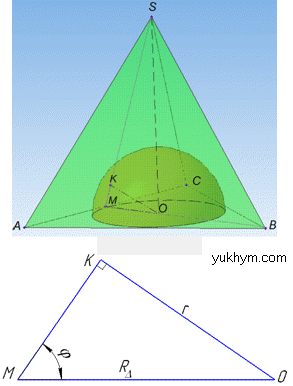
Розв'язання: Маємо тетраедр SABC з ребром A=3√6 (тетраедр – правильна трикутна піраміда, у якої всі ребра рівні).
Маємо сферу, яка дотикається до бічних граней тетраедра (зокрема в точці K дотикається до грані SAC) і має O, що лежить на основі ΔABC.
Проведемо два перпендикуляри:
MO⊥AC і KO⊥(SAC), тоді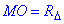 
– радіус вписаного кола з центром O (це інше коло, яке не є перерізом заданої сфери), KO=r – радіус сфери, оскільки радіус перпендикулярний до дотичної грані в точці дотику.
Відрізок KM лежить на прямій SM (апофема тетраедра) і відрізок MO лежить на прямій BM (BM=SM), оскільки ΔABC – рівносторонній (у тетраедра всі грані рівносторонні трикутники), тоді MO⊥MK.
Звідси слідує, що ∠SMB=∠KMO=φ – кут нахилу бічної грані тетраедра до площини основи. SO – висота тетраедра, тому SO⊥(ABC), тобто SO⊥MO.
Із рівностороннього трикутника ΔABC зі стороною A=3√6 обчислимо радіус вписаного кола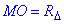 
та апофему BM=SM:
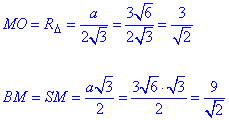
Розглянемо прямокутний ΔSMO (∠SMO=90), у якого SM=9/√2 – гіпотенуза, MO=3/√2 – катет прилеглий до кута ∠KMO=φ.
За означенням косинуса гострого кута прямокутного трикутника знайдемо cos(ϕ) і sin(ϕ):
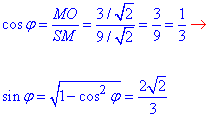
Розглянемо прямокутний ΔMKO (∠MKO=90), де MO=3/√2 – гіпотенуза.
За означенням синуса гострого кута прямокутного трикутника знайдемо KO=r – катет прилеглий до ∠KMO=φ:
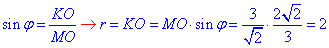
Отже, r=2 – радіус заданої сфери.
Відповідь: 2.
На практиці Вам можуть зустрітися як складніші, так і прості у порівнянні з наведеними завдання на визначення радіуса кулі.
Тому уважно розбирайте відповідь за відповіддю, щоб у Вас не виникали питання "як ми отримали радіус кулі в кожній із наведених тестових задач?"
