Функція f(x) називається неперервною в точці х=а, якщо:
1) вона визначена в цій точці;
2) існує границя функції в цій точці
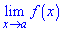
3) значення границі дорівнює значенню функції в точці х=а, тобто
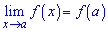
Якщо одна із умов порушується, то функція називається розривною в точці х=а, а сама точка х=а називається точкою розриву. Усі елементарні функції є неперервними на інтервалах визначеності.
КЛАСИФІКАЦІЯ ТОЧОК РОЗРИВУ
Точка х0 називається точкою розриву першого роду функції у = f(x), якщо існують скінчені односторонні границі справа
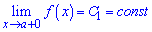
та зліва
.
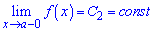Якщо, крім того, виконується хоча б одна із умов
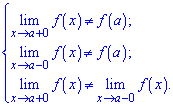
то функція в точці х=а має неусувний розрив першого роду.
Якщо границі функції рівні проте функція не існує
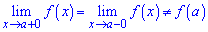
то маємо усувний розрив першого роду.
Точка х0 називається точкою розриву другого роду функції у= f(x), якщо границя справа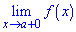 
або зліва 
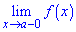не існує або нескінченна.
Стрибком функції в точці розриву х=х0 називається різниця її односторонніх границь
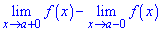
якщо вони різні.
Правила знаходження точок розриву функції
1) елементарна функція може мати розрив тільки в окремих точках, але не може бути розривною на певному інтервалі.
2) елементарна функція може мати розрив в точці де вона не визначена за умови, що вона буде визначена хоча би з однієї сторони від цієї точки.
3) неелементарна функція може мати розриви як в точках, де вона невизначена, так і в тих, де вона визначена.
Наприклад, якщо функція задана кількома різними аналітичними виразами (формулами) для різних інтервалів, то на межі стику може бути розривною.
Приклади знаходження точок розриву функції
Завдання 1.Знайти точки розриву функції
а)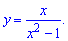 
Розв'язання: Функція визначена в усіх точках крім тих де знаменник перетворюється в нуль x=1,x=-1. Область визначення функції наступна
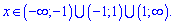
Знайдемо односторонні границі в точках розриву
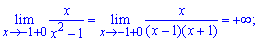
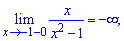
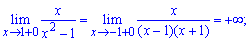
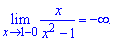
При знаходженні односторонніх границь подібного вигляду достатньо переконатися в знаку функції та в тому, що знаменник прямує до нуля. В результаті отримаємо границю рівну безмежності або мінус безмежності.
Оскільки в точках x=1,x=-1 функція має нескінченні односторонні границі, то аргументи x=1,x=-1 є точками розриву ІІ роду. Графік функції наведено на рисунку нижче
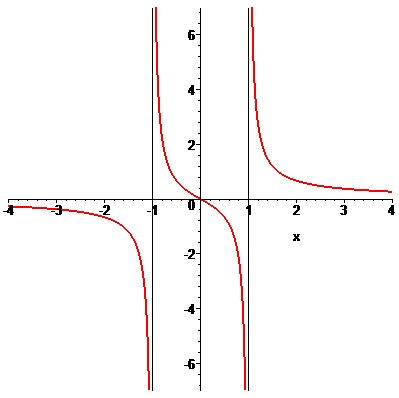
б)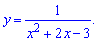 
Розв'язання: Завдання подібне до попереднього. В першу чергу знаходимо нулі знаменника
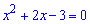
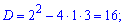
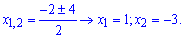
Таким чином функція визначена на всій дійсній осі за виключенням точок x=-3; x=1, які є точками розриву. Обчислимо односторонні границі справа та зліва
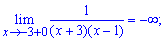
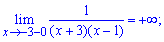
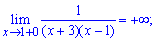
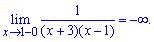
Границі функції нескінченні, тому, за означенням, маємо точки розриву x=-3; x=1 другого роду.
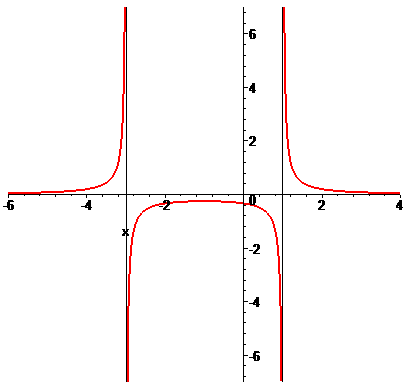
Із графіків наведених функцій бачимо, що для ряду з них відшукання точок розриву еквівалентне знаходженню вертикальних асимптот. Але бувають функції, які і без вертикальних асимптот мають розриви першого чи другого роду.
в)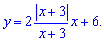 
Розв'язання: Задана функція неперервна на всій числовій осі крім точки x=-3. Обчислимо односторонні границі в цій точці
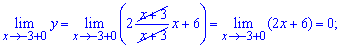
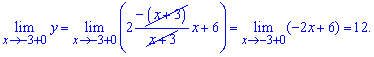
Вони різняться за значеннями, проте є скінченними. Отже точка x=-3 є неусувною точкою розриву І роду.
Завдання 2.Знайти точки розриву функції, якщо вони існують. Обчислити стрибок функції в точці розриву. Побудувати графік функції.
а)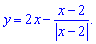 
Розв'язання:Для заданої дробової функції з модулем в знаменнику точка x=2 є точкою розриву. Знайдемо границі, щоб визначити характер розриву
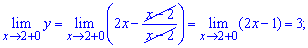
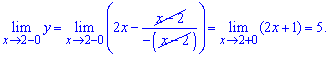
За означенням, точка x=2 є неусувною точкою розриву першого роду. Обчислимо стрибок функції при x=2
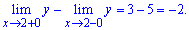
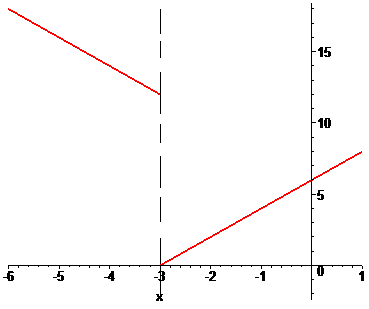
Графік функції на інтервалі, який нас цікавить наведено далі
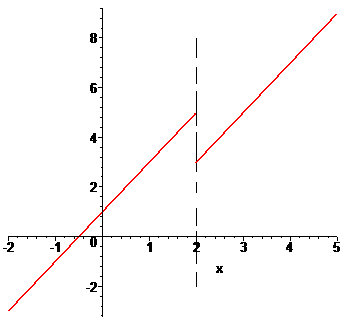
б)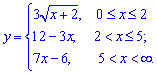 
Розв'язання: Неелементарна функція y(x) визначена для всіх невід'ємних значень аргументу. Точки, які розбивають функцію на інтервали можуть бути розривами. Для перевірки знайдемо відповідні границі
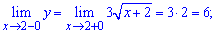
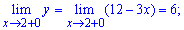
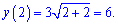
Оскільки границі в точці x=2 рівні значенню функції в цій точці, то функція – неперервна.
Звідси також слідує, що для вихідної функції стрибок рівний 6-6=0.
Дослідимо на неперервність другу точку
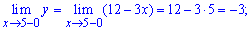
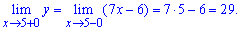
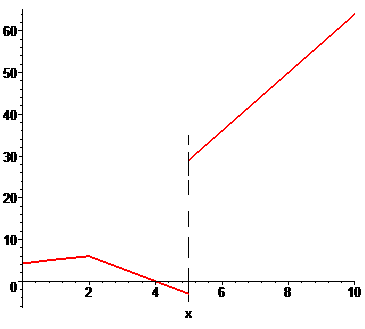
За означенням функція в точці x=2 має неусувний розрив І роду.
Стрибок функції рівний 29-(-3)=31.
Для заданої функції побудовано графік.
З наведеного матеріалу Ви повинні навчитися знаходити розриви першого та другого роду, а також розрізняти їх. Для цього підібрано небагато прикладів, які в повній мірі розкривають всі важливі питання теми. Все решта зводиться до знаходження простих односторонніх границь і не повинно бути для Вас складним.
