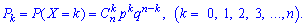
В табличной форме этот закон имеет следующий вид:

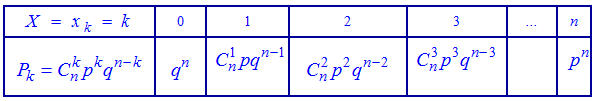
При проверке выполнения условия нормировки используется формула бинома Ньютона, поэтому закон распределения называют биномиальным

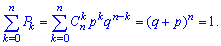
Построим вероятностную образующую функцию для этого закона

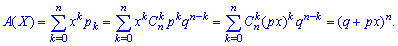
Итак, вероятностная образующая функция для биномиального закона ровна

Найдем основные числовые характеристики для этого закона

1. Математическое ожидание случайной величины через образующую функцию для биномиального распределения вычисляем по формуле

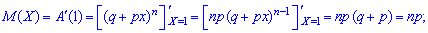
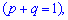
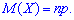
2. Вторая производная от образующей функции для биномиального распределения в единице примет значение

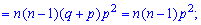
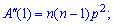
На основе найденного значения можно вычислять дисперсию

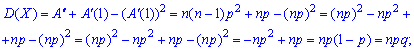
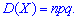
Имея дисперсию нетрудно установить среднее математическое отклонение

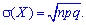
3. Коэффициент асимметрии А(Х) и эксцесс Е(Х) для биномиального распределения определяют по формулам

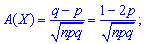
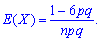
В случае роста количества испытаний n асимметрия и эксцесс стремятся к нулю.

Перейдем к практической стороне биномиального распределения

Задача 1. В партии однотипных деталей стандартные составляют 97%. Наугад из партии берут 400 деталей. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение М(Х), D(X), S(Х) для дискретной случайной величины Х — появления числа стандартных деталей среди 400 наугад взятых.

Решение. Целочисленных случайная величина Х имеет биномиальное закон распределения вероятностей, которая может принимать значения Х = k = 0, 1, 2, ..., 400. Вероятности возможных значений для данной задачи определяются по формуле Бернулли и составляют 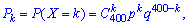где р = 0,97 — вероятность появления стандартной детали, q = 1 – p =1 – 0,97 = 0,03 — вероятность появления нестандартной детали. Согласно приведенным выше формулам определяем нужные величины:

------------------------------------

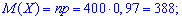
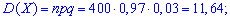
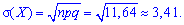
Задача 2. Два ювелирные заводы производят свадебные кольца в объеме 3:7. Первый завод производит 95% колец без дефекта, второй – 90%. Молодая пара перед свадьбой покупает пару колец. Построить закон распределения, вычислить математическое ожидание и среднее квадратичное отклонение.

Решение. Вероятность события А – куплена кольцо оказалась качественной определим по формуле полной вероятности

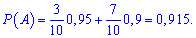
Случайная величина Х – количество колец надлежащего качества среди купленных имеет биномиальное закон распределения с параметрами

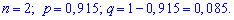
Найдем соответствующие вероятности

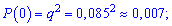
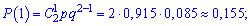
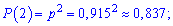
Запишем таблицу распределения

На основе табличных данных вычисляем математическое ожидание

дисперсию

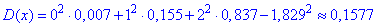
Среднее квадратичное отклонение

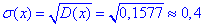
Как можно убедиться из примеров, биномиальний закон распределения простой как для понимания так и для вычислений. Хорошо разберитесь с примерами и пользуйтесь биномиальным распределением там где это необходимо.

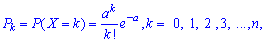
вычисляется по формуле Пуассона, где a=np<10. Как правило, Пуассоновское распределение касается вероятности появления благоприятного события в большом количестве экспериментов, если в одном - вероятность успешного завершения стремится к нулю.

В табличной форме этот закон распределения имеет вид

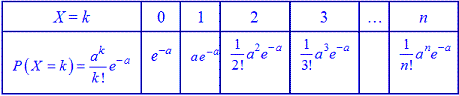
Условие нормировки для пуассоновского закона распределения запишется следующим образом

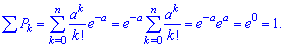
Построим образующую функцию вероятностей для приведенного закона

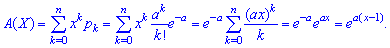
Она принимает достаточно простой компактный вид

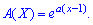
Воспользовавшись зависимостями для определения математического ожидания М (Х) и дисперсии D (X) через производные от образующей функции в единице, получим их простые зависимости

1. Математическое ожидание определяется по формуле

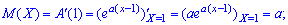
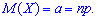
2. Имея вторую производную от образующей функции в единице

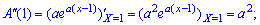
находят дисперсию

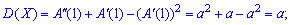
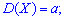
Среднее квадратическое отклонение вычисляем через квадратный корень из дисперсии

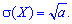
Следовательно, для пуассоновского закона распределения вероятностей математическое ожидание и дисперсия равны произведению количества опытов на вероятность благоприятной события

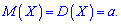
На практике, если математическое ожидание и дисперсия близкие по значению то принимают гипотезу, что исследуемая величина имеет закон распределения Пуассона.

3. Асимметрия и эксцесс для пуассоновский закон также уровни и вычисляются по формулам

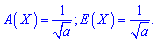
Рассмотрим несколько задач.

----------------------------------------

Задача 1. Микропроцессор имеет 10000 ранзисторов, работающих независимо друг от друга. Вероятность того, что транзистор выйдет из строя во время работы прибора, является величиной маловероятной и составляет 0,0007. Определить математическое ожидание М (Х) и среднее квадратическое отклонение S (Х) случайной величины Х — исла транзисторов, выйдут из строя во время работы процессора.

Решение. Задача удовлетворяет всем законам пуассоновский распределения:

количество испытаний n=10000 велика;

вероятность р=0,0007 близка к нулю;

их произведение a=np=7<10.

На основе данных вычисляем заданные величины

------------------------------------

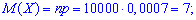
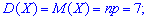
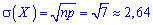
Задача 2. В рыбацком городке 99,99% мужчин хотя бы раз в жизни были на рыбалке. Проводят социологические исследования среди 10000 наугад выбранных мужчин. Определить дисперсию D (X) и среднее квадратическое отклонени S (Х) случайной величины Х — числа мужчин, которые ни разу не были на рыбалке.

Решение. егко убедиться, что величина Х имеет пуассоновский закон распределения. С условия задачи находим

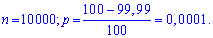
По формулам находим дисперсию и среднее квадратическое отклонение

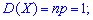
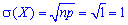
Можно найти в гугле еще много подобных задач, всех их объединяет изменение случайной величины по закону Пуассона. Схема нахождения числовых характеристик приведена выше и является общей для всех задач, кроме того формулы для вычислений достаточно простыми даже для школьников.

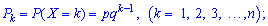
Есть во всех предыдущих опытах кроме k-го експернимент дал плохой результат и только в k-му был успешным. Данную формулу вероятностей называют геометрическим законом распределения, поскольку правая его часть совпадает с выражением общего элемента геометрической прогрессии.

В табличной форме геометрический закон распределения имеет вид

При проверке условия нормировки используется формула суммы бесконечной геометрической прогрессии

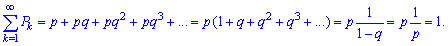
Вероятностную образующую функцию выражаем по формуле

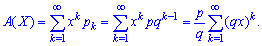
Поскольку 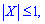то образующую функцию можно просуммировать

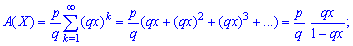
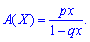
Числовые характеристики для геометрического закона распределения вероятностей определяют по формулам:

1. Математическое ожидание

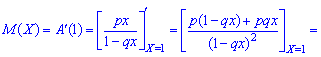
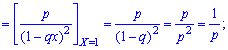
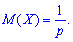
2. Дисперсию и среднее квадратическое отклонение по формулам

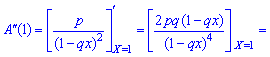
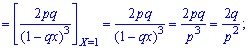
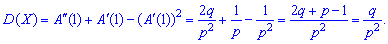
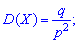
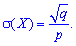
3. Коэффициент асимметрии и эксцесса для геометрического распределения определяют по формуле

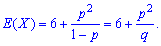
Среди дискретных случайных величин только геометрическому закону дано свойство отсутствия последействия. Это означает, что вероятность появления случайного события в k-ом эксперименте не зависит от того, сколько их появилось до k-го, и всегда равна p.

--------------------------------------

Пример 1. Игральная кость подбрасывается до первого появления цифры 1. Определить все числовые характеристики М (Х), D (X), S (Х), A(X), E(X) для случайной величины Х числа осуществляемых подбрасываний.

Решение. По условию задачи случайная величина Х вляется целочисленной с геометрическим закон распределения вероятностей. Вероятность успешного подбрасывания величина постоянная и равна единице разделенной на количество граней кубика

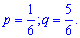
Имея p,q необходимые числовые характеристики Х находим по приведенным выше формулам

------------------------------------

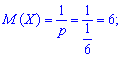
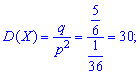
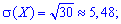
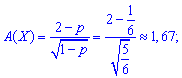
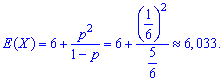
Пример 2. Охотник-любитель стреляет из ружья по неподвижной мишени. Вероятность попасть в мишень при одном выстреле является величиной постоянной и равна 0,65. Стрельба по мишени ведется до первого попадания.

Определить числовые характеристики М (Х), D (X), S (Х), A(X), E(X) числа израсходованных охотником патронов.

Решение. Случайная величина Х подчиняется геометричниму закона распределения поэтому вероятность попадания в каждой попытке постоянна и составляет p=0,65;q=1-p=0,35.

По формулам вычисляем математическое ожидание

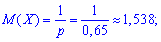
дисперсию

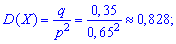
среднее квадратическое отклонение

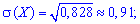
асимметрию

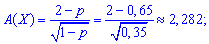
эксцесс

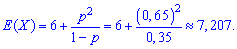
Вычисление числовых характеристик для геометрического закона распределения не так сложны, поэтому пользуйтесь приведенным формулам в подобных задачах и получайте только правильные результаты.

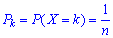
В табличной форме записи равномерный закон распределения имеет вид:

Условие нормировки для равномерного закона распределения имеет вид

Вероятностная образующая функция на основе первой формулы принимает значение

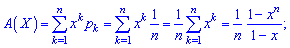
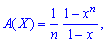
или

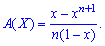
Числовые характеристики равномерного закона находим на основе образующей функции

1. Математическое ожидание находим по формуле

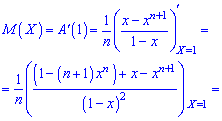
При х = 1 получаем неопределенность 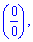которую раскрываем по правилу Лопиталя

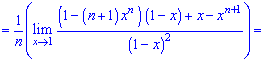
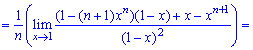
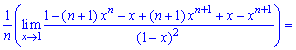
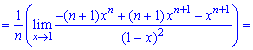
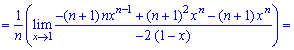
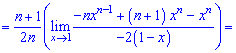
При х = 1 нова имеем неопределенность вида 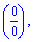которую также раскрываем по правилу Лопиталя

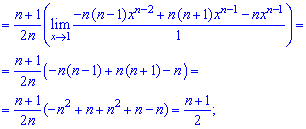
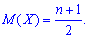
Вычисление заняли богатая времени, однако формула для математического ожидания получилась довольно легкой.

2. Выполнив подобные, но более громоздкие преобразования, дисперсию и среднее математическое отклонение находим по формулам

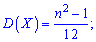
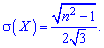
3. Для равномерного распределения вероятностей асимметрия и эксцесс равны нулю

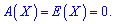
Есть и другое определение, согласно которому функция имеет равномерное распределение, если некотором интервале плотность вероятностей принимает постоянное значение

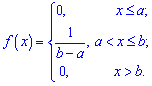
Функция распределения вероятностей для равномерного закона определяется интегрированием

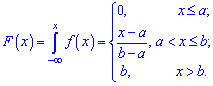
Математическое ожидание в таких случаях определяют зависимости

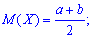
дисперсию по формуле

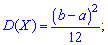
и среднее квадратическое отклонение через корень

Вероятность попадания случайной величины Х в некоторый интервал 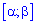, содержащийся внутри интервала 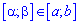определяется по формуле

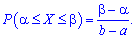
Приведенные формулы часто являются применимыми на практике чем те, которые были даны выше.

Рассмотрим примеры отыскания числовых характеристик.

------------------------------------------

Пример 1. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение М (Х), D (X), S (Х), Найти математическое ожидание, дисперсию и среднее квадратическое отклонение Х имеет равномерный закон распределения и возможные значения ее значение лежит в диапазоне 1..50:

.

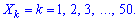Решение. По условию задачи имеем следующие данные n = 50, p = 1/50=0,02.

Согласно формулам вычисляем математическое ожидание

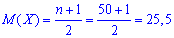
дисперсия

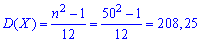
среднее квадратическое отклонение

-------------------------------------------

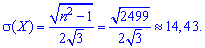
Пример 2. Поезда в метро прибывают на станцию ??каждые 10 минут. Определить вероятность того, что время ожидания состава не будет больше 4 минуты.

Решение. По условию задачи имеем два интервала

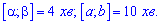
Согласно формуле, искомая вероятность равна доле этих величин

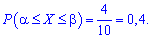
Задачи на отыскание интервала попадания случайной величины, распределена по ривнимирним законом решайте по такой же схеме. Она проста и не требует сложных вычислений.

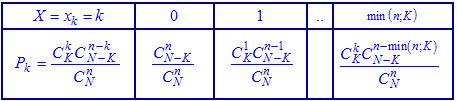
Пусть задано некоторое множество однотипных элементов, число которых равно N; из них K элементов имеют, например, признак А (цвет, стандартность, наполнения), а остальные N-K элементов - признак В. С этого множества наугад берут n еэлементов. Случайная величина X – число элементов с признаком вида А, что случается среди n наугад взятых элементов. Тогда X принимает значения k=0,1,2,...,min(n,K) , а вероятность их появления определяется гипергеометрическим законом распределения

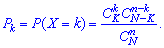
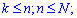
В табличной форме записи этот закон распределения имеет вид

Напомним, что сочетание находим по формуле

а факториал функцию по правилу–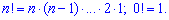

При n=k і k=0 сочетание равное единице.

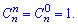
Условие нормировки для гипергеометрического распределения имеет вид

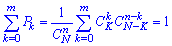
В зависимости от условия задачи наименьшее значение может составлять m = 0, 1, 2, 3, ..., m.

Числовые характеристики этого закона вычисляются по приведенным ниже формулам:

1. Математическое ожидание

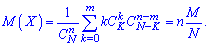
2. Дисперсия и среднее квадратическое отклонение

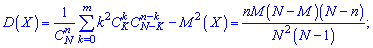
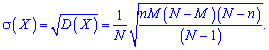
3. Для асимметрии

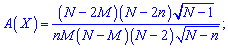
и эксцесса

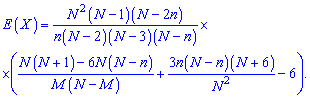
формулы имеют довольно громоздкий вид, поэтому их, как правило, вычисляют в Эксель, или математических программах (Maple, MathCad, Mathematica).

Рассмотрим несколько примеров на применение приведенных выше формул

-----------------------------------------

Пример 1. В ящике содержится 10 однотипных деталей, из них 7 стандартных, а остальные являются бракованными. Наугад из ящика берут m деталей. Построить законы распределения целочисленной случайной величины Х — появление числа стандартных деталей среди m наугад взятых и вычислить математическое ожидание М(Х), дисперсию D (X), и среднее математическое отклонение S(Х), если:

I. m = 3; II) m = 4; III) m = 5; IV) m = 7.

Решение. Используя формулу (253) построим гипергеометрические законы распределения:

I. Имеем следующие начальные условия для случая выбора трех деталей

n = 3; N=10; K= 7; N-K= 3; k = 0, 1, 2, 3.

В табличной форме гипергеометрический закон для этих данных имеет вид

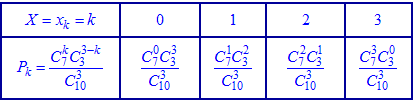
или после вычисления сочетаний

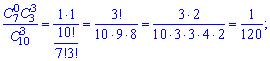
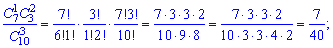
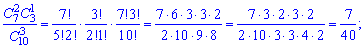
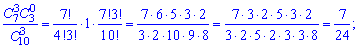
в виде таблицы вероятностей

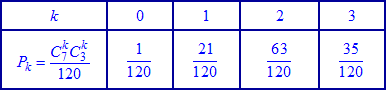
Условие нормирования

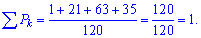
выполняется, следовательно все верно посчитано. Не ленитесь проверять его, оно намного скорее укажет Вам на присутствие ошибки при неправильной правой части. Вычисляем числовые характеристики:

Математическое ожидание

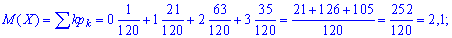
Дисперсию

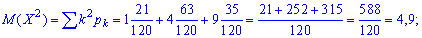
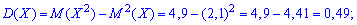
Среднее квадратичное отклонение

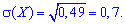
ІІ. Выбирают четыре детали

n = 4; K= 7; N-K= 3; k = 1, 2, 3, 4.

В табличной форме закон распределения запишется формулами

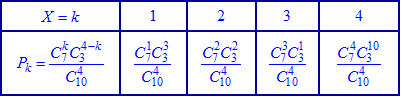
или после вычислений в виде таблицы

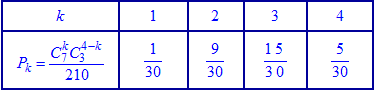
Проверяем условие нормировки для найденных значений

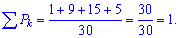
Оно выполняется, следовательно можем вычислять числовые характеристики по приведенным выше формулам:

математическое ожидание примет значение

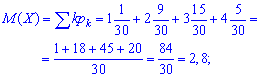
дисперсию и среднее квадратичное отклонение определяем по схеме предыдущей задачи

.

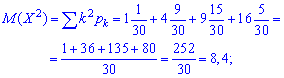
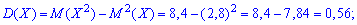
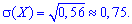ІІІ. Выбирают пять деталей

т = 5; K = 7; N-K = 3; k = 2, 3, 4, 5.

В табличной форме закон подается в виде

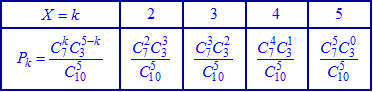
или таблицы значений

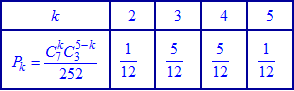
Условие нормирования

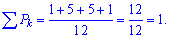
выполняется. Вычисляем математическое ожидание

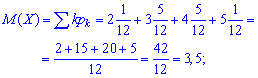
Составляющую дисперсии

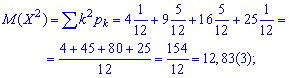
дисперсию и среднее квадратичное отклонение

.

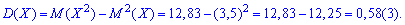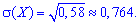
IV.) Выбирают семь деталей

т = 7; K= 7; N-K= 3; k = 4, 5, 6, 7.

В табличной форме данное деление принимает значение

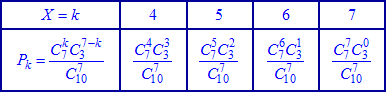
или после вычислений

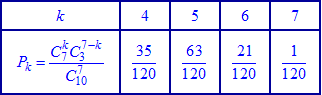
Условие нормирования

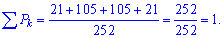
выполняется.

Числовые характеристики определяем на основе формул:

математическое ожидание

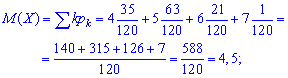
математическое ожидание квадрата величины

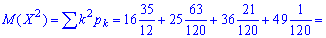
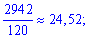
дисперсию

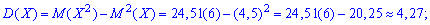
среднее квадратичное отклонение

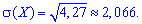
На этом решение задачи завершено. Будьте внимательны при решении примеров на гипергеометрическое распределение, поскольку достаточно часто требуется находить сочетание 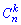и при упрощении факториалов можно допустить ошибку.