Для начала выберем задание из сборника задач Дубовика В.П., Юрика І.І. "Высшая математика".

-----------------------------------

Примеры

Решить систему линейных алгебраических уравнений.

1) (1. 153)

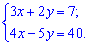
2) (4. 165)

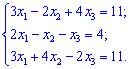
3) (4. 174)

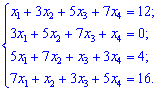
Решение.

1) В случае двух уравнений решение можно получить более простым способом. Выражаемый из второго уравнения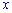

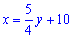
и подставим в первое

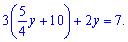
Раскрыв скобки, сгруппируем подобные слагаемые

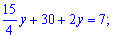
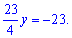
Отсюда получим решение

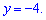
Переменную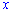найдем подстановкой 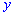в любое из уравнений

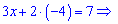
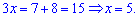
Таким образом решением системы двух уравнений будут следующие значения

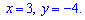
Поскольку цель статьи научить студентов решать по методике Крамера то решим данный пример и етим методом.

Для этого выпишем систему линейных уравнений в виде

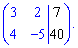
Найдем детерминант основной части

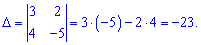
Для вычисления вспомогательных определителей ставим столбец свободных членов на место первой строки для 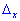и на место второй для 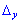. В результате получим

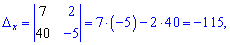
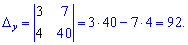
Подставим найденные значения в формулы Крамера

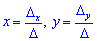
и найдем неизвестные

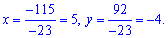
Из рассмотренного примера видим что вычисление при двух уравнениях с двумя неизвестными достаточно простые.

2) Запишем систему трех алгебраических уравнений в удобном для решения виде

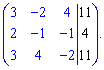
Найдем детерминант системы по правилу треугольников

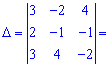
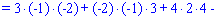
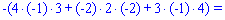
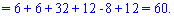
Для вычисления дополнительных определителей подставляем столбец свободных членов на место первого, второго и третьего столбцов. В результате получим

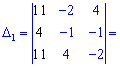
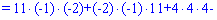
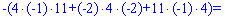
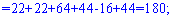
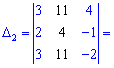
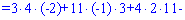
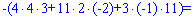
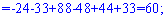
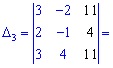
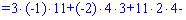
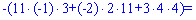
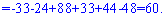
Вычисляем неизвестные за формулами Крамера

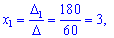
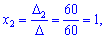
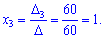
Для данного примера нахождения решения также не слишком сложно, хотя по сравнению с системой двух уравнений вычислений заметно прибавилось.

3) Записываем систему уравнений четвертого порядка в виде

Находим главный определитель системы. При вычислении детерминантов четвертого порядка их необходимо раскладывать за строками или столбцами у каторых больше всего нулей. Поскольку в данном случае нулей главный определитель не имеет то разложим его за первой строкой

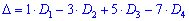
и найдем соответствующие детермиінанты третьего порядка

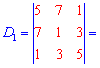
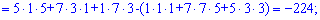
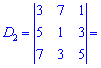
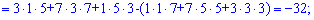
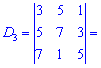
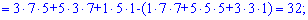
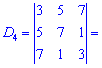
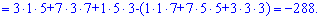
Подставим найденные значения в определитель

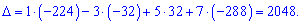
По такой же схеме вычисляем вспомогательные определители, напомню лишь, что они образуются заменой столбца в главном определителе на столбец свободных членов (обозначен черным цветом). Я не буду приводить детальных излаганий, однако Вы можете проверить, что детерминанты примут значение

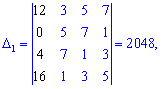
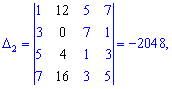
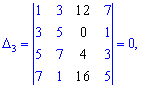
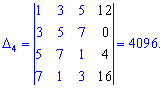
Подставив в формулы Крамера, после вычислений будем иметь

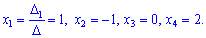
На этом пример решено.

Системы четырех линейных уравнений наиболее трудоемкие в вычислениях, для вычисления их решения нужно решать 5*4 определители третьего порядка, в то время как системы трех уравнений лиш 4. Будьте внимательные при вычислениях ведь самая малая ошибка может иметь следствием неверный результат.

----------------------------------------------

Посмотреть материалы:

• Матричный метод решения системы линейных уравнений
• Метод Гаусса
• Метод Крамера
• Решение СЛАУ 3-4 порядка матричным методом
• Решение методом Гаусса СЛАУ 3-5-ого порядка

к треугольному виду

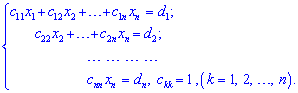
Предположим, что в системе коэффициент . Если это условие не выполняется, то на первое место переносим уравнение, которое ее удовлетворяет. С помощью первого уравнения исключим из остальных уравнений.

Для этого делят первую строчку на , обозначим

.

Дальше второй строки вычитаем первую строку, умноженную на ;от третьего первую строчку, умноженный на ; и так далее до последней строки. Получим таблицу коэффициентов:

Для неизвестных имеем систему уравнений. Выполняя, как и раньше, исключим из всех уравнений, начиная с третьего. Для этого сначала разделим вторую строчку на .

Если коэффициент , то переставим уравнения так, чтобы выполнялось условие .

Обозначив

,

от третьей строки вычтем вторую строчку, умноженный на ;

от четвертой строки вычтем вторую строчку, умноженный на и т.д. Получим таблицу коэффициентов:

Продолжая процесс исключения неизвестных получим таблицу:

Таблица коэффициентов при неизвестных сводится к треугольному виду. Все главной диагонали элементы . Запишем соответствующую систему уравнений:

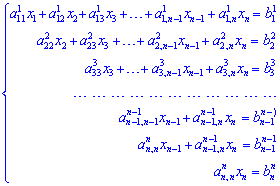
Переход от первой системы уравнений до последней называется прямым ходом метода Гаусса. Обратный ход метода Гаусса начинается с последней системы уравнений. Ее решают с конца до начала. Из последнего уравнения находят . Подставив это значение в предпоследнее - находят и т.д. Из первого уравнения находят .

Если система уравнений с неизвестными имеет единственное решение, то эта система всегда может быть преобразована к треугольному виду. Для студентов не всегда требуют, чтобы диагональные элементы были равны единице. Достаточно просто свести систему линейных уравнений к верхней треугольной.

--------------------------------------------

Пример 1.

Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Гаусса.

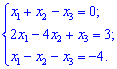
Решение.

Исключим неизвестную из второго и третьего уравнения. Для этого от них вычтем первое умноженное на

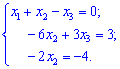
Видим, что наше уравнение в таком виде можно решать обратным ходом метода Гаусса. Для этого из последнего уравнения выразим

Подставим полученное значение в предыдущее уравнение и найдем

Из первого уравнения находим

Решение данной системы равен

-----------------------------------------

В случаях систем больших размеров, а также для удобства, часто на практике используют другую схему решения. Вместо преобразований над системой выполняют соответствующие преобразования над матрицей, составленной из коэффициентов при неизвестных и столбца из свободных членов, который для удобства выделяют вертикальной линией. Такую матрицу называют расширенной матрицей системы.

-----------------------------------------

Пример 2.

Решить систему четырех линейных алгебраических уравнений методом Гаусса.

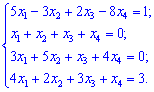
Решение.

Выпишем расширенную матрицу для данной системы

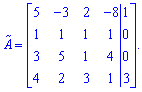
Сведем ее к треугольному виду с помощью элементарных преобразований.

1.Поменяем местами первый и второй строки.

2. Добавим к элементам второго, третьего и четвертого строк элементы первой строки, умноженные соответственно на

3. Поменяем местами второй и третий строки. Добавим к элементам третьего и четвертого строк элементы второй строки, умноженные соответственно на

4. От четвертого уравнения умноженного на вычитаем третье уравнение умноженное на

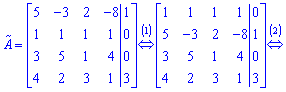
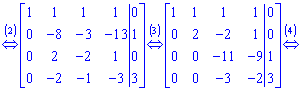
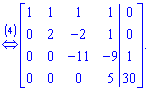
Такой расширенной матрицы соответствует следующая система уравнений

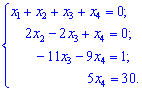
С четвертого уравнения находим и подставляем в третье уравнение

Найденные значения подставляем во второе уравнение

Из первого уравнения находим первую неизвестную

Система полностью решена и – ее решение.

-----------------------------------------------------

Посмотреть материалы:

• Матричный метод решения системы линейных уравнений
• Метод Крамера
• Решение методом Крамера СЛАУ 3-4-го порядка
• Решение СЛАУ 3-4 порядка матричным методом
• Решение методом Гаусса СЛАУ 3-5-ого порядка

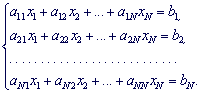
Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй - при котором из неизвестным он находится.

Если определитель матрицы не равен нулю

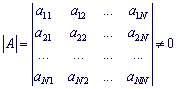
то система линейных алгебраических уравнений имеет единственное решение.

Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство.

Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной

Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае - несовместимой.

Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной.

Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.

Эквивалентные преобразования СЛАУ

1) перестановка местами уравнений;

2) умножение (или деление) уравнений на отличное от нуля число;

3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.

Решение СЛАУ можно найти разными способами.

МЕТОД КРАМЕРА

ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:

- определители, образованные с заменой -го столбца, столбцом из свободных членов.

Если , а хотя бы один из отличен от нуля, то СЛАУ решений не имеет. Если же , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.

---------------------------------------------------------------

Задача 1.

Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера

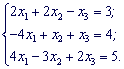
Решение.

Найдем определитель матрицы коэффициентов при неизвестных

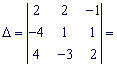
Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:

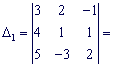
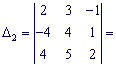
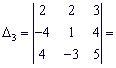
По формулам Крамера находим неизвестные

Итак единственное решение системы.

Задача 2.

Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.

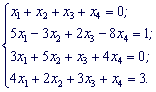
Решение.

Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.

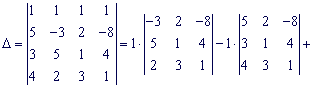
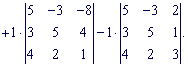
Найдем составляющие определителя:

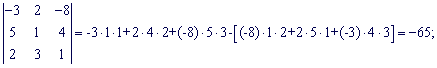
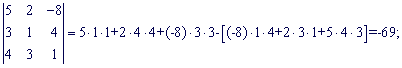
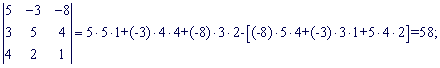
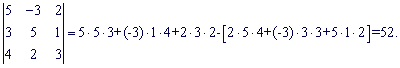
Подставим найденные значения в определитель

Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:

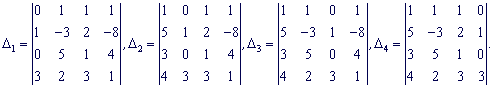
Разложим каждый из определителей по столбцу в котором есть больше нулей.

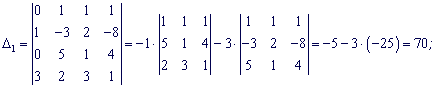
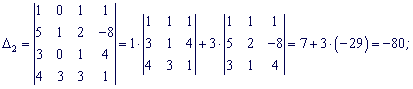
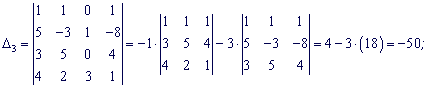
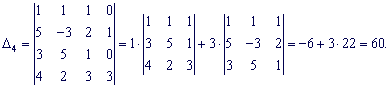
По формулам Крамера находим

Решение системы

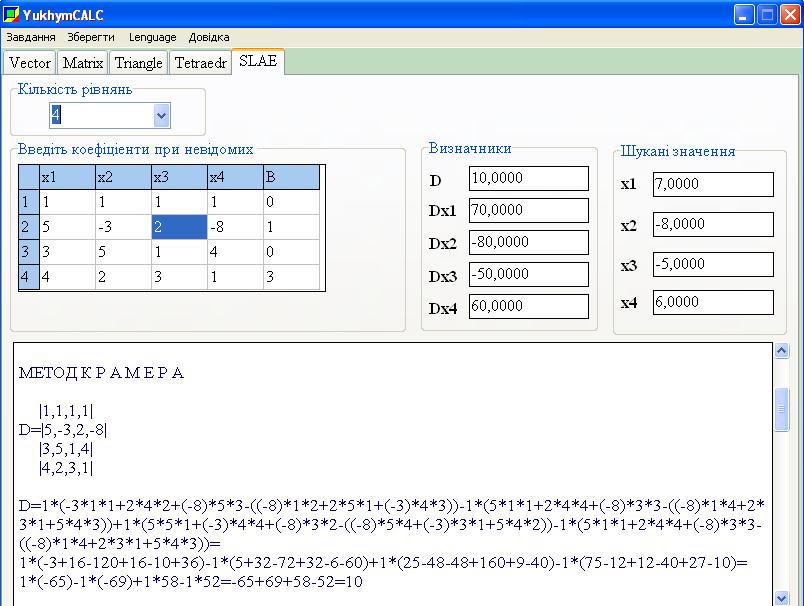
Данный пример можно решить математическим калькулятором YukhymCALC . Фрагмент программы и результаты вычислений наведены ниже.

-----------------------------

МЕТОД К Р А М Е Р А

|1,1,1,1|

D=|5,-3,2,-8|

|3,5,1,4|

|4,2,3,1|

D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10

|0,1,1,1|

Dx1=|1,-3,2,-8|

|0,5,1,4|

|3,2,3,1|

Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70

|1,0,1,1|

Dx2=|5,1,2,-8|

|3,0,1,4|

|4,3,3,1|

Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80

|1,1,0,1|

Dx3=|5,-3,1,-8|

|3,5,0,4|

|4,2,3,1|

Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50

|1,1,1,0|

Dx4=|5,-3,2,1|

|3,5,1,0|

|4,2,3,3|

Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60

x1=Dx1/D=70,0000/10,0000=7,0000

x2=Dx2/D=-80,0000/10,0000=-8,0000

x3=Dx3/D=-50,0000/10,0000=-5,0000

x4=Dx4/D=60,0000/10,0000=6,0000

Посмотреть материалы:

• Матричный метод решения системы линейных уравнений
• Метод Гаусса
• Решение методом Крамера СЛАУ 3-4-го порядка
• Решение СЛАУ 3-4 порядка матричным методом
• Решение методом Гаусса СЛАУ 3-5-ого порядка

{jcomments on}

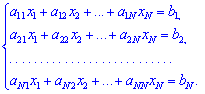
Обозначим через – матрицу-столбец неизвестных, через –матрицу-столбец свободных членов. Тогда впереди систему уравнений можно записать в виде матричного уравнения:

Если квадратная матрица имеет отличный от нуля определитель ,то для нее существует обратная . Умножив слева в этом уравнении на , получим

Учитывая, что и, получим матричный решение системы

Нахождение матричного решения называется матричным способом решения системы линейных алгебраических уравнений (СЛАУ).

---------------------------------------------------------------

Пример 1.

Решить СЛАУ матричным методом.

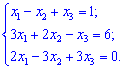
Решение.

Обозначим матрицу и векторы

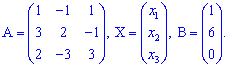
Матричный решение системы уравнений ищем по формуле

Для нахождения обратной матрицы вычислим определитель

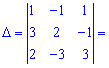
Поскольку , то заданная система уравнений совместная и имеет единственное решение.

Найдем транспонированную матрицу

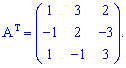
Найдем алгебраические дополнения к элементам заданной матрицы:

Обратную матрицу вычисляем по формуле

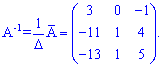
Найдем решение СЛАУ

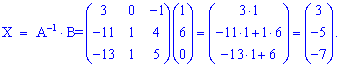
Решение СЛАУ:

Посмотреть материалы:

• Метод Гаусса
• Метод Крамера
• Решение методом Крамера СЛАУ 3-4-го порядка
• Решение СЛАУ 3-4 порядка матричным методом
• Решение методом Гаусса СЛАУ 3-5-ого порядка

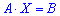
где 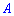-матрица, составленная из коэффициентов при неизвестных; 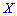- столбец неизвестных; - столбец свободных членов. После того, если для матрицы 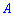существует обратная матрица 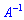( 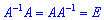) то система линейных уравнений имеет единственное решение и он находится за формулой

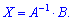
Поскольку перемножить матрицу на вектор столбец не складывает особенных трудностей, то большая проблема при вычислениях - найти обратную матрицу

В нахождении решения за приведенной формулой и заключается суть матричного метода.

Рассмотрим несколько примеров из сборника задач Дубовика В.П., Юрика І.І. "Высшая математика"

-----------------------------------

Задача.

Решить систему линейных алгебраических уравнений.

1) (1. 183)

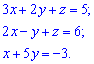
2) (4. 182)

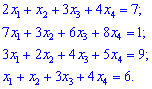
Решение.

1) Запишем систему трех линейных уравнений в матричной форме

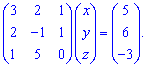
Найдем обратную матрицу. Напомним, что

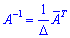
где 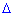- определитель матрицы 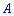, а 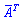- транспонированная матрица алгебраических дополнений элементов 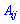определителя матрицы.

Вычислим определитель матрицы

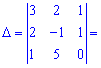
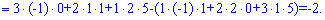
Матрица алгебраических дополнений 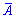состоит из элементов 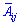, которые вычисляются через миноры по правилу

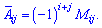
Миноры 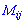- это определители на порядок меньшие от определителя 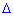, которые образуются вычеркиванием в нем 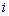-й строки и 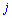- го столбца. На первый взгляд звучит слишком запутано, но при вычислениях все станет понятно и просто.

Найдем алгебраические дополнения к определителю

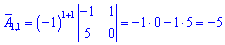
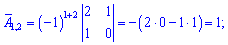
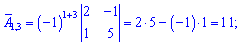
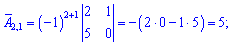
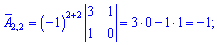
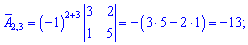
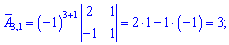
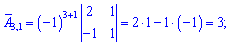
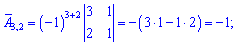
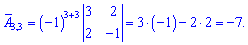
Запишем найденную матрицу алгебраических дополнений

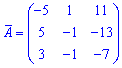
и протранспонируем ее

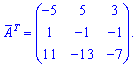
Находим обратную матрицу

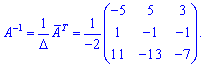
С помощью обратной матрицы находим решение системы линейных уравнений

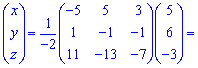
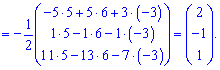
На етом решения примера завешено. Как видите никаких сложных вычислений в етом задании мы не делали.

2) Запишем систему линейных уравнений четвертого порядка в матричной форме

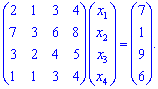
Поскольку все коэффициенты ненулевые то вычислять ее будет трудно. Выполним над системой линейных уравнений элементарные превращения чтобы превратить в нуль некоторые из коэффициентов.

От второй строки отнимем первую и последнюю строки

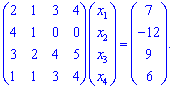
От третьей строки отнимем сумму первой и четвертой строки начальной системы

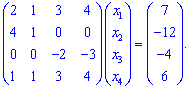
От четвертой строки отнимем первый

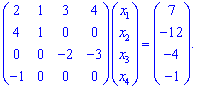
Из последней строки уже можем сказать что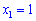 но будем придерживаться правил чтобы научиться решать большие системы уравнений.

Поскольку матрица стала разреженной то вычисление определителя и матрицы алгебраических дополнений упростятся. Найдем определитель матрицы, разложив его за четвертой строкой

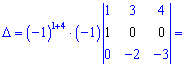
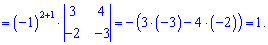
Найдем матрицу алгебраических дополнений, раскладывая искомые детерминанты за строками и столбцами которые содержат больше всего нулей. Для самопроверки выпишу Вам вычисление только первой строки. Остальные попробуйте вычислить самостоятельно

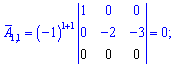
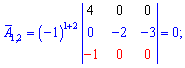
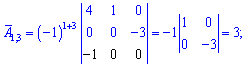
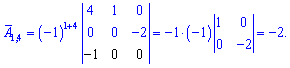
После нахождения всех значений получим следующую матрицу дополнений

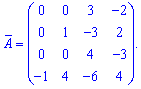
Поскольку определитель равен единице то обратная матрица с транспонированной матрицей дополнений совпадают

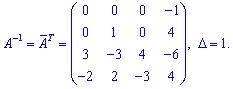
Подставим в матричную запись и найдем решение

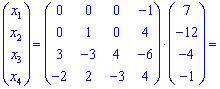
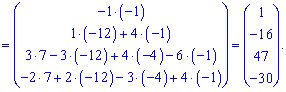
При вычислениях систем линейных алгебраических уравнений третьего, четвертого порядка матричным методом придется находить большое количество алгебраических дополнений , которые собой являют определители второго и третьего порядка соответственно. Именно ошибки при их вычислении чаще всего становятся причиной неверного решения. Для избежания таких ситуаций нужно хорошо знать правила нахождения определителей второго, третьего порядка, а также правила чередования знаков возле миноров.

Изучайте их и получайте лишь верные решения !

----------------------------------------------

Посмотреть материалы:

• Матричный метод решения системы линейных уравнений
• Метод Гаусса
• Метод Крамера
• Решение методом Крамера СЛАУ 3-4-го порядка
• Решение методом Гаусса СЛАУ 3-5-ого порядка

Рассмотрим примеры решения систем линейных уравнений методом Гаусса, взяв за справочник сборник задач Дубовика В.П., Юрика И.И. "Высшая математика".

-------------

Задача.

Решить систему линейных алгебраических уравнений.

1) (1. 189)

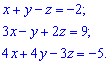
2) (4. 195)

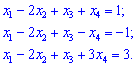
3) (4. 198)

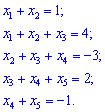
Решение.

1) Преобразуем исходную систему к ступенчатому виду. Для этого от второго уравнения вычтем первое, умноженное на 3, а от четвертого вычтем первое, умноженное на 4.

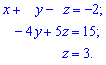
В результате с третьего уравнения имеем 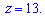Полученное значение подставляем в исходное уравнение для нахождения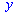

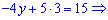
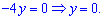
Полученные значения 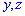подставляем в первое уравнение

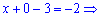
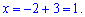
Решением системы трех линейных уравнений будут следующие значения переменных

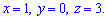
2) Имеем систему трех уравнений с четырьмя неизвестными. В таких случаях одна переменная может быть свободна, а остальные будут выражаться через нее. Сведем систему к ступенчатому виду. Для этого от второго и третьего уравнения вычтем первое

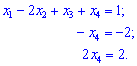
Из последних двух уравнений получаем идентичные решения

.

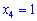После подстановки в первое уравнение получим

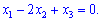
Данное уравнение связывает три переменные. Таким образом любая из переменных может быть выражена через две других

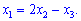
Итак получим следующее решение

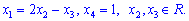
3) Имеем разреженную систему линейных уравнений пятого порядка с пятью неизвестными. Сведем ее к ступенчатому виду. От второго уравнения вычтем первое и запишем в удобном для анализа виде

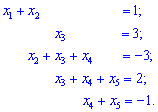
Из второго уравнения находим, что 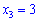. Подставляем значения во все нижние уравнения и переносим за знак равенства. Также поменяем второе с третьим уравнения местами

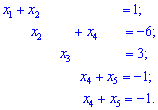
Четвёртое и пятое уравнения эквивалентны. Выразим одну из переменных через другую

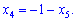
Полученное значение подставим во второе уравнение и найдем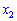

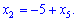
Из первого уравнения определяем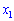

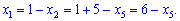
Решение системы уравнений следующее

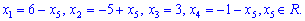
При вычислениях систем линейных алгебраических уравнений методом Гаусса нужно свезти систему линейных уравнений к ступенчатому виду. Для этого удобно записывать переменные под переменными, как в последнем примере, это ускорит решение. Остальное все зависит от матрицы, которую нужно решить и Ваших умений.

----------------------------------------------

Посмотреть материалы:

• Матричный метод решения системы линейных уравнений
• Метод Гаусса
• Метод Крамера
• Решение методом Крамера СЛАУ 3-4-го порядка
• Решение СЛАУ 3-4 порядка матричным методом