Запишем правила дифференцирования

1)

2)

3)

4)

5)

6)

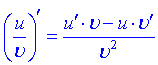
Здесь – постоянная величина (константа) , – функции от аргумента , имеющие производные.

7) Если – сложная функция, то есть , а , и существуют отдельно производные и, то существует производная от по , причем

Используя это, таблицу формул дифференцирования запишем так

8)

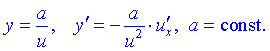
9)

10)

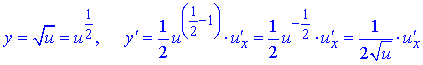
11)

12)

13)

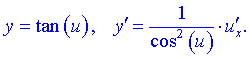
14)

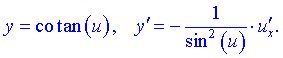
15)

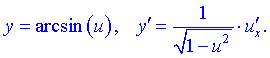
16)

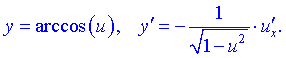
17)

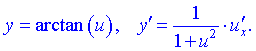
18)

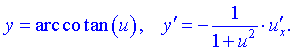
19)

20)

21)

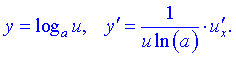
22)

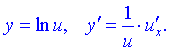
23)

В следующих статьях будут приведены примеры дифференцирования, учитывая приведенную таблицу.

Пример 1.

Вычислить производные

1)

2)

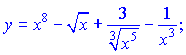
3)

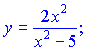
4)

5)

6)

7)

Решение.

1) По формулам дифференцирования (1), (3), (9) получим

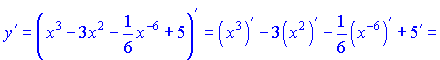
2) Вводим дробные и отрицательные степени и превращаем заданную функцию к виду

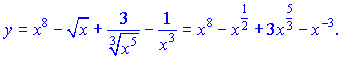
Используя формулы (3), (4), (9) находим

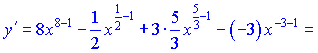
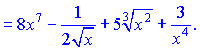
3) Данный пример вычисляем по правилу (6)

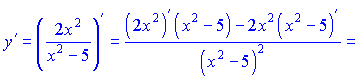
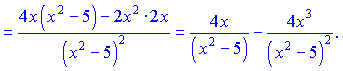
4) Производную функции ищем по правилу сложной функции (7)

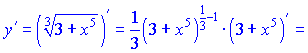
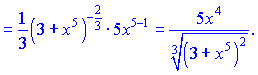
5) Производные от функции

находим по правилу производной от произведения функций, и правилом производной от сложной функции

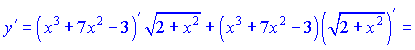
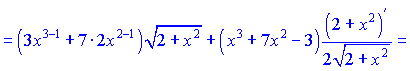
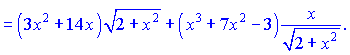
6) По правилу производной от сложной функции будем иметь

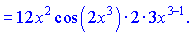
7) Много студентов которые еще толком не знают правил, сначала подносят к квадрату выражение в скобках

а затем проводят дифференцировки. Это неправильно, долго и трудно. Воспользовавшись правилом дифференцирования сложной функции получим

Если Вы будете подносить к квадрату, а затем дифференцировать то получите многочлен, который еще предстоит свести к компактному виду. Результат будет правильный, но зачем идти сложным путем, если за нас уже давно придумали правила дифференцирования, которые упрощают вычисления.

Изучайте их и пользуйтесь на практике.

В таких случаях целесообразно обе части выражения сначала прологарифмировать по основанию , а затем приступить к дифференцировке. Этот способ получил название логарифмического дифференцирования. Производную логарифма функции называют логарифмической производной. Суть метода с помощью формул можно описать следующим образом:

имеем сложную функцию вида

к обеим сторонам применяем логарифмирования

находим производные правой и левой части равенства

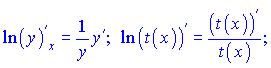
Приравниваем производные и выражаем

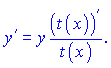
В этом суть метода, дальше все зависит от функции .

Если она представляет собой произведение функций

то по свойствам логарифма он будет равен сумме логарифмов

Если имеем дробь от функций

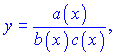
то применяя логарифмирования получим

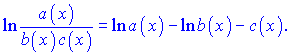
Если имеем функцию в степени другой

то по свойствам логарифма получим

В случае корней дифференцировки значительно упрощается

Дальнейшее вычисление производных зависит от сложности самих функций. Рассмотрим конкретные примеры, чтобы данный материал стал для Вас более понятным и наглядным.

Задача.

Используя логарифмирования найти производную (Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")

1) (5.2.178)

2) (5.2.191)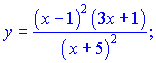

3) (5.2.195)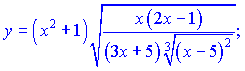

4) (5.2.199)

Решение.

Примеры выбрано сложные для того, чтобы раскрыть всю силу метода логарифмического дифференцирования и рассмотреть типичные распространенные примеры.

1) Проведем логарифмирования левой и правой частей

Найдем производную правой части

Производная левой части показана при изложении теоретического материала. Записываем обе части

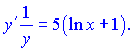
Далее переносим функцию из знаменателя в правую часть и не забываем поменять ее значение

Несмотря на сложный вид данный пример полностью решено.

2) Используем свойства логарифма к данному примеру

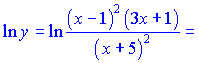
Проводим дифференцирования обеих частей равенства

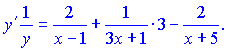
Сведем к общему знаменателю правую сторону. В результате математических операций получим

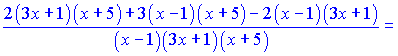
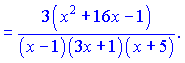
Подставим в исходную равенство, перенеся функцию в правую часть

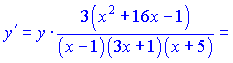
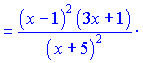
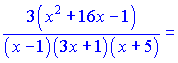
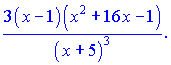
В результате ряда несложных математических манипуляций получили достаточно компактный конечный результат производной. При исчислении данного примера направления подобный результат пришлось бы искать очень долго.

3) Несмотря на сложный вид данное выражение, на основе свойств степеней, можно переписать в следующем виде

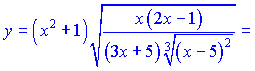
Применим к нему логарифмирования

Производная от правой части будет равна следующему выражению

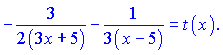
Здесь для упрощения дальнейших выкладок введено обозначение .

Учитывая производную , окончательно получим

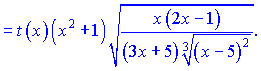
Можно оставлять в таком виде, поскольку суть данного урока научиться применять метод логарифмического дифференцирования. Но если Вы захотите для упрощения свести все к общему знаменателю, то получите следующее выражение

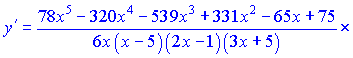
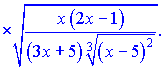
Поверьте это займет у Вас много времени.

4) Проводим логарифмирования функции

Дальше по методике находим производную правой части. Она будет равна выражению

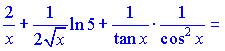
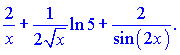
Подставляя в формулу для производной от , получим

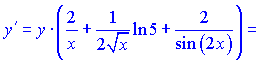
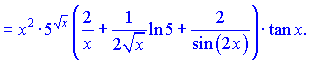
На этом решения примера завершен.

Практикуйте с подобными задачами и через некоторое время у Вас не будет никаких трудностей с такого сорта примерами.

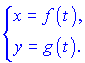
Производная заданной функции первого порядка находится по правилу

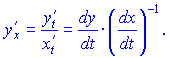
Вторая производная определяется зависимостью

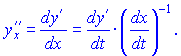
Аналогичным образом можно вывести производные старших рядом.

Рассмотрим несколько примеров для закрепления материала на практике.

Пример 1.

Найти производные функций, заданных параметрически.

(Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")

1) (5.253)

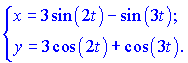
2) (5.256)

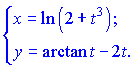
3) (5.261)

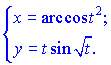
4) (5.263)

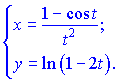
Решение.

1) Вычислим производные функции и аргумента по параметру

Найденные значения подставляем в формулу

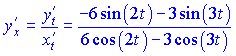
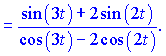
В данном случае, чтобы не выносить знак минус перед дробь, умножим на знаменатель и переставим слагаемые так, чтобы первыми шли положительные. Сама же кривая на плоскости будет иметь вид

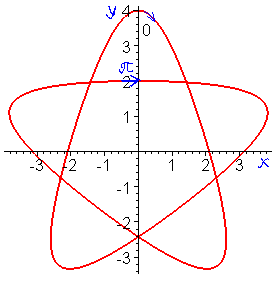
2) Найдем производные по параметру

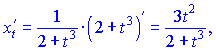
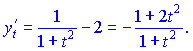
Вычисляем значение производной

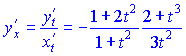
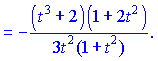
Пример не сложный, главное правильно вычислить производные.

3) Вычисляем производные

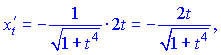
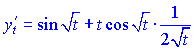
Полученные значения подставим в формулу для производной

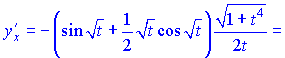
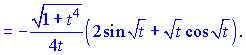
4) Продифференцируем функцию и аргумент по параметру

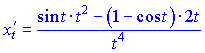
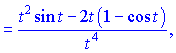
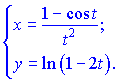
Полученные значения подставляем в формулу и упрощаем числитель и знаменатель на

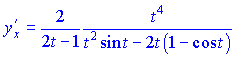
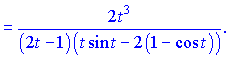
Из примеров видно, что вычисление производной от параметрически заданной функции не слишком сложное. Следуйте последовательности выполнения действий, будьте внимательны при упрощении выражений и все у Вас получится правильно.

из которой нельзя отделить саму функцию. В этом случае функция называется неявной функцией от.

Однако саму производную функции по переменной можно вычислить. Для этого дифференцируют функцию по , при этом учитывают, что сама функция зависит от переменной . Из полученного уравнения группируют слагаемые, содержащиеся при производной и выражают ее.

Для закрепления материала рассмотрим следующие примеры.

Пример 1.

Найти производные функций, заданных неявно (Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")

1) (5.219)

2) (5.223)

3) (5.227)

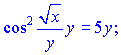
4) (5.236)

Решение.

1) Продифференцируем правую и левую части

Полученное выражение разделим на общий множитель и сгруппируем слагаемые, содержащие производную и перенесем их в одну сторону за знак равенства. В результате получим

Поделив на множитель при производной получим ее значение

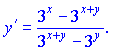
Для упрощения, вынесем из числителя и знаменателя общие множители исоответственно. В результате будем иметь

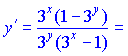
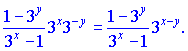
Как видите ничего сложного мы не делали но быстро нашли производную неявно заданной функции. Рассмотрим следующую задачу.

2) Проведем дифференцировки

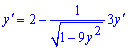
Выделяем слагаемые, содержащие производную

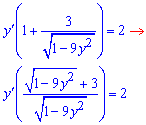
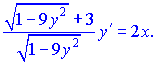
Разделим на множитель при производной и найдем ее значение

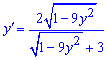
Задача полностью решена.

3) Вычислим производную правой и левой части

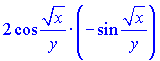
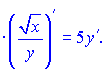
Найдем производную частки функций

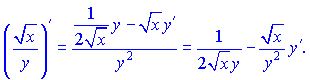
Первых два множителя равны синусу двойного угла. Поэтому производные можем записать в виде

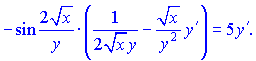
Умножим правую и левую части на чтобы избавиться знаменателей и сгруппируем слагаемые при производной

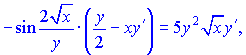
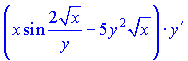
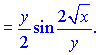
Из последней зависимости находим значение искомой производной

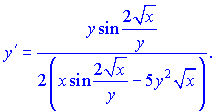
В такого рода примерах главное не ошибиться при отыскании производных.

4) Проведем дифференцирования функций

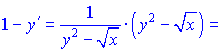
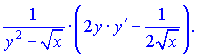
Выделим слагаемые, содержащие и сгруппируем их

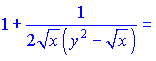
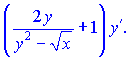
Сведем выражения к общему знаменателю

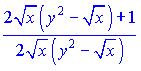
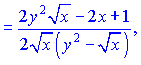
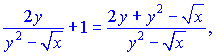
и подставим их на свои места

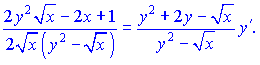
Отсюда выразим производную

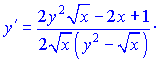
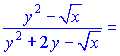
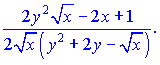
На этом решения примера завершено.

При вычислении производной неявно заданной функции типичными ошибками на практике являются неправильное взятие производной и неразбериха со знаками при группировке подобных слагаемых. Будьте внимательны в таких ситуациях и не допускайте ошибок.

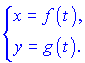
Производная заданной функции первого порядка находится по правилу

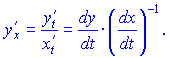
Вторая производная определяется зависимостью

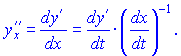
Аналогичным образом можно вывести производные старших порядков.

Рассмотрим несколько примеров для закрепления материала на практике.

-------------------------------------------

Пример 1.

Найти производные функций заданных параметрически.

(Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")

1) (5.253)

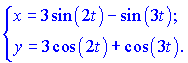
2) (5.256)

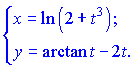
3) (5.261)

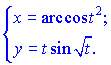
4) (5.263)

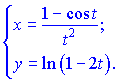
Решение.

1) Вычислим производные функции и аргумента по параметру

Найденные значения подставляем в формулу производной

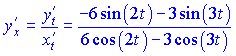
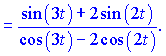
В данном случае, чтобы не выносить знак минус перед дробь, домножили на знаменатель и переставили слагаемые так, чтобы первыми шли положительные. Сама же кривая на плоскости будет иметь вид

2) Найдем производные по параметру

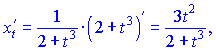
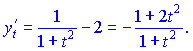
Вычисляем значение первой производной

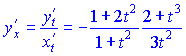
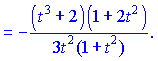
Пример не сложен, главное правильно вычислить производные.

3) Вычисляем производные

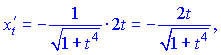
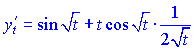
Полученные значения подставим в формулу для производной

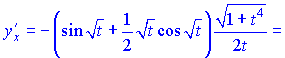
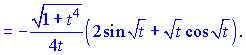
4) Продифференцируем функцию и аргумент по параметру

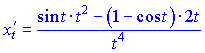
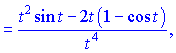
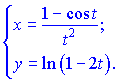
Полученные значения подставляем в формулу и упрощаем числитель и знаменатель по параметру

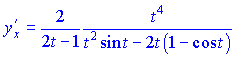
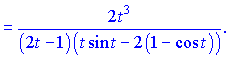
Из примеров видно, что вычисление производной от параметрически заданной функции не слишком сложное задание, главное знать формулы. Придерживайтесь последовательности выполнения действий, будьте внимательны при упрощении выражений и все у Вас получится правильно.

----------------------------------------------------

Под производной высших порядков понимают дифференцирования функции более одного раза. Если производнуюповторно дифференцировать, то получим производную второго порядка, или вторую производную функции , и она обозначается

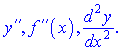
Производная третьего порядка будет иметь вид

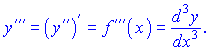
Аналогично получают формулы для нахождения производных высших порядков. При нахождении производной порядке необходимо иметь производную порядка. Исключение составляют функции для которых можно заметить тенденцию изменения производных. Это степенные, некоторые тригонометрические и экспоненциальные функции:

В других случаях, для нахождения производных высших порядков от заданной функции нужно последовательно находить все ее производные низших порядков. Для практического усвоения материала рассмотрим примеры.

Пример 1.

Вычислить производные второго порядка

1)

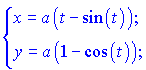
2)

3)

4)

Решение.

1) По правилам дифференцирования параметрических функций имеем

Применим к заданной функции. Найдем производную

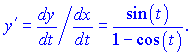
Дифференцируем второй раз. По правилу дифференцирования получим

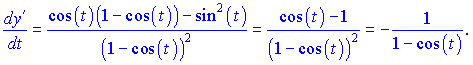
По формуле вычисляем

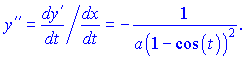
2)Определяем первую производную для функции

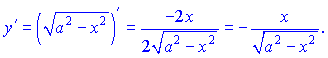
Вычисляем вторую производную

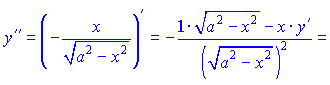
3)Вычислим первую производную

а потом вторую

При нахождении производной второго и высших порядков для данного примера и ему подобных можно пользоваться следующим правилам:

1) если степень функции меньше порядка производной , то она вклада не дает

2) все старшие степени дают вклад

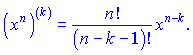
По такой схеме вторую производную можно было найти так:

Для практики второй способ эффективнее, особенно если нужно найти производные гораздо более высоких порядков чем второй.

4) Производную функции первого порядка будет иметь вид

второго порядка

По аналогии можно вывести формулу для производной экспоненциальной функции порядка

Решая примеры для синус и косинус функций можно заметить сходство при исчислении старших производных и вывести следующие зависимости

Пользуйтесь и пусть не возникают проблемы с производными высших порядков.