-----------
Решение многих задач математики, экономики, статистики, механики, сводится к решению систем линейных алгебраических уравнений.
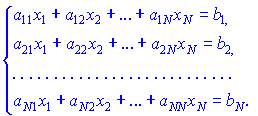
В результате вычислений получаем, что система одно решение, множество или нет ни одного. Давайте выясним от чего это зависит? Рассмотрим, для примера два линейных уравнения с двумя неизвестными:
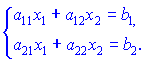
неизвестными Для решения этих уравнений мы должны умножить их на соответствующие множители, при которых исключается одно из неизвестных ![]() или
или![]() : первое на
: первое на ![]() минус второй на
минус второй на ![]() для нахождения
для нахождения ![]() ; второе на
; второе на ![]() минус первое на
минус первое на ![]() для нахождения
для нахождения ![]()
![]()
![]()
На основе этого
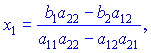
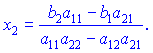
Эти выражения верны при условии, что знаменатель не равен нулю
![]()
Если![]() ,то система уравнений или нет решения, или имеет бесконечное количество решений. Выражение в знаменателе (
,то система уравнений или нет решения, или имеет бесконечное количество решений. Выражение в знаменателе (![]() ), которые являются одинаковыми при двух неизвестных, называют определителем и обозначают
), которые являются одинаковыми при двух неизвестных, называют определителем и обозначают
![]()
Определителем второго порядку называется число, равное разнице произведений элементов главной и вспомогательной диагоналей, т.е
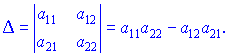
Определителем третьего порядка находят по правилу треугольников 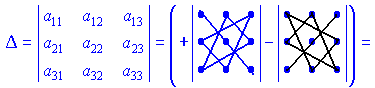
![]()
Это правило легко запомнить, если дописать рядом с определителем первый и второй в столбце.
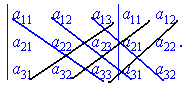
Данный метод вычисления определителя третьего порядка называется правилом Саррюса. В процессе вычислений систем линейных уравнений установлено, что определители равны сумме слагаемых, которые определяются как произведение элементов, взятых по одному одновременно с каждой строки и столбца. Для системы трех уравнений в произведение входит три элемента, четырех - четыре и т. д. Количество слагаемых в определителе в общем равна факториала числа уравнений. В случаях нулевых коэффициентов при неизвестных нахождения определителя упрощается. Для вычисления определителей старших порядков используют правила.
--------------------------------------------
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
1. Величина определителя не изменится, если его строки заменить столбцами, причем каждая строка заменяют столбиком с тем же номером (транспонирования).
2. Если в определителе поменять местами только две строки (или два столбца), то определитель меняет знак на противоположный, сохраняя свое абсолютное значение.
3. Если определитель имеет два одинаковых колонки или два одинаковых строки, то он равен нулю.
4. Если определитель содержит два пропорциональных строк (столбцов), то его значение равно нулю. Если элементы некоторого строки (столбца) равны нулю, то и сам определитель равен нулю.
5.Если все элементы некоторого строки (столбца) умножить на постоянное число, то значение определителя также умножится на это число. Отсюда следует, что общий множитель всех элементов строки (столбца) можно вынести за знак определителя.
--------------------------------------------
Определитель![]() -го порядка, по правилу, равный сумме произведений элементов произвольного строки или столбца на соответствующие алгебраические дополнения. Мысленно вычеркнем в определителе
-го порядка, по правилу, равный сумме произведений элементов произвольного строки или столбца на соответствующие алгебраические дополнения. Мысленно вычеркнем в определителе ![]() -го порядка
-го порядка ![]() -й строчку и
-й строчку и ![]() -й столбец, а из оставшихся элементов создадим определитель(
-й столбец, а из оставшихся элементов создадим определитель(![]() )-го порядка с сохранением размещения строк и столбцов. Полученный определитель называется минором определителя и обозначается
)-го порядка с сохранением размещения строк и столбцов. Полученный определитель называется минором определителя и обозначается ![]()
Алгебраическое дополнение ![]() элемента
элемента![]() определителя можно представить в виде
определителя можно представить в виде
![]()
--------------------------------------------
Пример 1.
Задачи. Найти определитель 4-го порядка
![]()
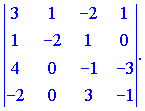
Решение.
Разложим определитель по элементам второго столбца 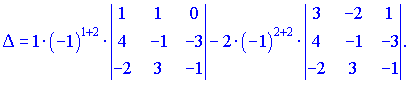
Первый определитель разложим по первой строкой
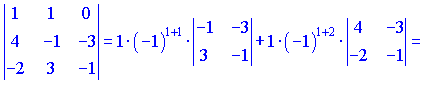
![]()
Второй вычислим по правилу
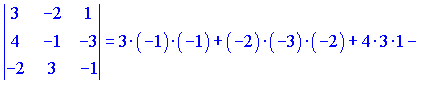
![]()
![]()
Подставляя в формулу для определителя, получим
![]()
Студенческий калькулятор YukhymCALC осуществляет вычисления и выводит результат, быстрее чем Вы сможете ввести соответствующие матрицы. В результате получим следующий результат
*** Матрицы ***
Определитель матрицы
Входные данные
A=(3;1;-2;1)
(1;-2;1;0)
(4;0;-1;-3)
(-2;0;3;-1)
Det(A)=3*(-2*(-1)*(-1)+1*(-3)*0+0*0*3-(0*(-1)*0+1*0*(-1)+(-2)*(-3)*3))-1*(1*(-1)*(-1)+1*(-3)*(-2)+0*4*3-(0*(-1)*(-2)+1*4*(-1)+1*(-3)*3))-2*(1*0*(-1)+(-2)*(-3)*(-2)+0*4*0-(0*0*(-2)+(-2)*4*(-1)+1*(-3)*0))-1*(1*(-1)*(-1)+1*(-3)*(-2)+0*4*3-(0*(-1)*(-2)+1*4*(-1)+1*(-3)*3))=3*(-2+0+0+0+0-18)-1*(1+6+0+0+4+9)-2*(0-12+0+0-8+0)-1*(0-4+0+0+24+0)= 3*(-20)-1*(20)-2*(-20)-1*20=-60-20+40-20=-60
--------------------------------------------
------------------------------
]]>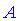 , элементы которой
, элементы которой 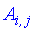 равны сумме попарных произведений элементов строки первой матрицы
равны сумме попарных произведений элементов строки первой матрицы 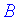 на соответствующие элементы столбца второй матрицы
на соответствующие элементы столбца второй матрицы  :
: 
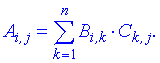
Из этого следует что перемножить между собой можно матрицы в которых количество столбцов первой 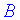 равно количеству строк второй
равно количеству строк второй  . Новая матрица
. Новая матрица 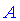 которая является произведением двух имеет размерность
которая является произведением двух имеет размерность 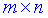 , где
, где 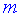 – количество строк первой матрицы, а
– количество строк первой матрицы, а 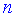 – столбцов второй. Правила достаточно просты и для нахождения произведения матриц нужно уметь лиш умножать и прибавлять. Рассмотрим несколько примеров из сборника задач Дубовика В.П., Юрика И.И. "Высшая математика".
– столбцов второй. Правила достаточно просты и для нахождения произведения матриц нужно уметь лиш умножать и прибавлять. Рассмотрим несколько примеров из сборника задач Дубовика В.П., Юрика И.И. "Высшая математика".
--------------------------------------------
Примеры.
Найти произведение матриц.
1) (1.110)
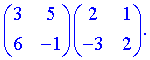
Для нахождения произведения умножаем строки первой матрицы на столбцы второй
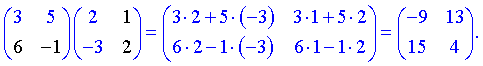
2) (1.112)
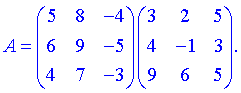
Найдем элементы новой матрицы.
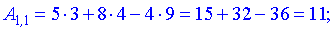
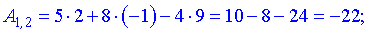
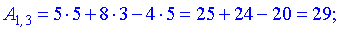
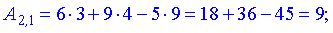
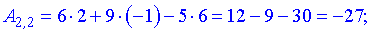
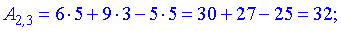
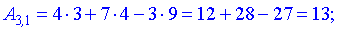
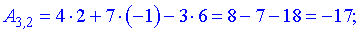
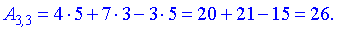
Записываем полученные значения в матрицу.
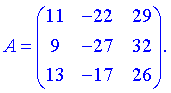
3) (1.114)
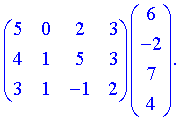
Согласно правилам - произведением будет матрица-вектор размерности 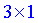 . Вычислим ее элементы
. Вычислим ее элементы
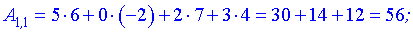
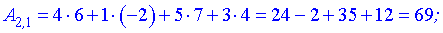
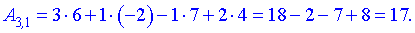
Окончательно матрица примет вид
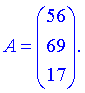
4) (1.115)
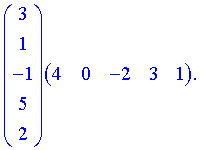
При вычислении произведения матриц-векторов получим квадратную матрицу размера. 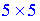 .
.
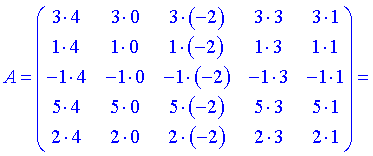
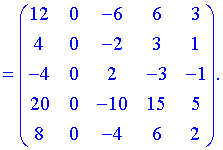
Простыми операциями умножения получили новую квадратную матрицу пятого порядка.
5) (1.116)
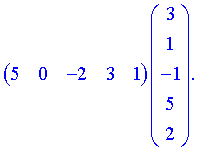
Результатом умножения в данном примере будет матрица которая содержит лиш один элемент.
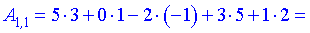
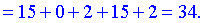
На этом практическая часть урока закончена. Упражняйтесь в решении подобных примеров, ведь умножения - это одна из основных операций (не только в матрицах). В следующих статьях материал будет сложнее, поэтому начинайте знакомиться с матрицами с простого.
]]>За справочник возьмем сборник задач Дубовика В.П., Юрика И.И. "Высшая математика". Позже будут добавлены примеры вычисления определителя матрицы из других источников.
--------------------------------------------
Примеры.
1) (1.4)
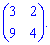
Применим правило вычисления определителя для матрицы второго порядка.
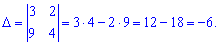
2) (1.6)
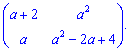
Выполним вычисления согласно правилу
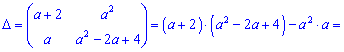
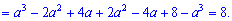
3) (1.8)
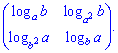
Данный пример выглядит сложным но со знанием следующих правил логарифма
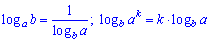
решается на удивление быстро.
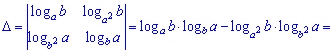
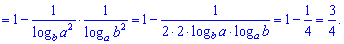
4) (1.14)
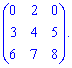
Вычислим данный определитель двумя способами: по правилу треугольников и через алгебраические дополнения.
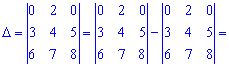
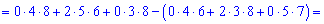
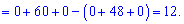
А сейчас разложим по элементам первого рядка, поскольку в нем больше нулей
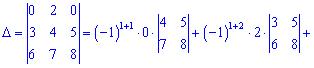
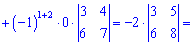
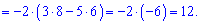
В этом примере специально выписаны дополнение у нулевых множителей, так как не все понимают откуда берутся дополнения. По правилу они равны определителю, который образуется вычеркиванием строки 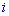 и столбца
и столбца 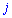 того элемента
того элемента 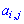 для которого ищутся, умноженному на минус единицу в степени
для которого ищутся, умноженному на минус единицу в степени
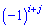 .
.
Схематически на примере матрицы четвертого порядка это выглядит так:
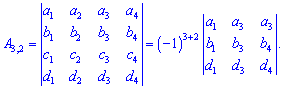
Внимательно посмотрите, какие элементы в определителе выписаны для дополнений и Вам все станет понятно.
Суть метода алгебраических дополнений заключается в том, что когда мы матрицу с нулевыми элементами может разложив ее по по строке или столбцу в котором больше нулей нам остается вычислить столько определителей на порядок меньших основной матрицы, сколько ненулевых элементов. Это значительно упрощает вычисления.
6) (1.19)
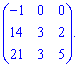
Если вычисления проводить по правилу треугольников, то получим много нулевых произведений. В такого рода примерах целесообразно использовать алгебраические дополнения.
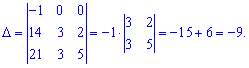
7) (1.21)
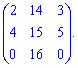
Вычислим определитель через алгебраические дополнения третьей строки
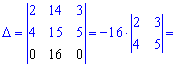
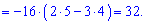
Как можно убедиться, решение с помощью алгебраических дополнений в случаях разреженных матриц можно получить быстро и без большого количества вычислений.
8) (1.58)
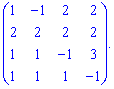
Выполним элементарные преобразования. От другого рядка вычтем первый, а от четвертого - третий. Получим разреженную матрицу
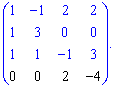
Определитель найдем через алгебраические дополнения к четвертой строке
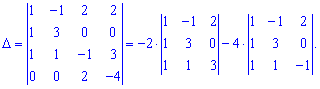
Вычислим каждый из слагаемых
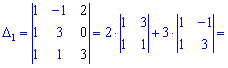
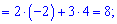
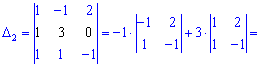
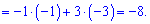
Подставляем в определитель
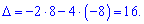
9) (1.72)
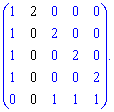
Найдем определитель через расписание по строкам и столбцам, содержащие нули (выделены черным).
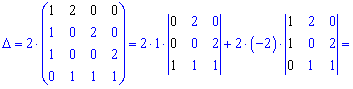
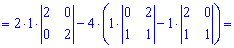
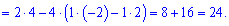
Таким методом нахождения определителя пятого порядка свелось к простым вычислениям. Практикуйте и изучайте правила и через некоторое время у Вас будет выходить не хуже. До встречи в следующих уроках!
----------------------------------------------
]]>СВОЙСТВА РАНГА МАТРИЦЫ
1. Ранг матрицы равен нулю только для нулевой матрицы. В других случаях ранг матрицы равен некоторому положительном числу.
2. Ранг прямоугольной матрицы не превышает меньшего из двух чисел ![]() и
и ![]() т.е.
т.е. ![]() .
.
3. Для квадратной матрицы ![]() -го порядка
-го порядка ![]() только тогда, когда матрица невырожденная.
только тогда, когда матрица невырожденная.
4. В случае квадратной матрицы если ![]() то определитель матрицы равен нулю.
то определитель матрицы равен нулю.
При нахождении ранга матрицы, как правило, нужно вычислять большое количество определителей. Чтобы облегчить задачу студентам давным-давно найдены элементарные преобразования с помощью которых можно слегка поменяв вид матрицы без вычисления определителей посчитать ранг.
ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ МАТРИЦЫ
1. Транспонирование, т.е. замена каждой строки столбцом с тем же номером и наоборот.
2. Перестановка двух строк или двух столбцов.
3. Умножение всех элементов строки или столбца на любое число не равное нулю.
4. Добавление всех элементов строки или столбца соответствующих элементов параллельного ряда, умноженного на одно и то же число.
Матрицы, полученные одна из второй элементарными преобразованиями называются эквивалентными. Эквивалентные матрицы не равны друг другу, но при элементарных преобразованиях матрицы ее ранг не меняется. Если матрицы ![]() и
и ![]() эквивалентны то это записывается так:
эквивалентны то это записывается так: ![]()
Рассмотрим два основных метода нахождения ранга матрицы.
Первый метод –- метод окантовки - заключается в следующем:
Если все миноры 1-го порядка, т.е. элементы матрицы равны нулю, то ![]() .
.
Если хоть один из миноров 1-го порядка не равен нулю, а все миноры 2-го порядка равны нулю то ![]() .
.
Если минор 2-го порядка отличен от нуля то исследуем миноры 3-го порядка. Таким образом находят минор ![]() -го порядка и проверяют, не равны ли нулю миноры
-го порядка и проверяют, не равны ли нулю миноры ![]() -го порядка.
-го порядка.
Если все миноры ![]() -го порядка равны нулю, то ранг матрицы
-го порядка равны нулю, то ранг матрицы ![]() равен числу
равен числу ![]() . Такие миноры
. Такие миноры ![]() -го порядка, как правило, находят путем "окантовки" минора
-го порядка, как правило, находят путем "окантовки" минора ![]() -го порядка.
-го порядка.
Второй метод определения ранга матрицы заключается в применении элементарных преобразований матрицы при возведении ее к диагональному виду. Ранг такой матрицы равно числу отличных от нуля диагональных элементов.
Рассмотрим примеры применения каждого метода.
--------------------------------------------------
Пример 1.
Задание. Найти ранг матрицы ![]() методом окантовки.
методом окантовки.
![]()

Решение. Матрица ![]() содержит ненулевые элементы миноры 1-го порядка, следовательно ее ранг может быть равен единице. Согласно правила ранг матрицы не превышает трем
содержит ненулевые элементы миноры 1-го порядка, следовательно ее ранг может быть равен единице. Согласно правила ранг матрицы не превышает трем ![]() . Минор 2-го порядка
. Минор 2-го порядка
![]()
равен нулю, но следующий минор
![]()
отличен от нуля. Окантовывая минор второго порядка проверим третий: для этого разложим его по третьей колонке
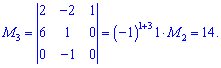
Рассмотрим минор четвертого порядка, окантовывает настоящее
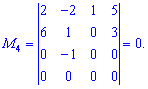
Он равен нулю, поскольку последняя строка нулевой. Остается вычислить еще один минор
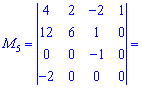
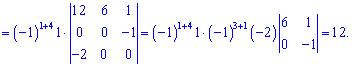
Искомый ранг матрицы равен четырем (![]() ). На примере можно видеть, что выбор окантовки не всегда можно удачно выбрать и нужно числить большое количество миноров.
). На примере можно видеть, что выбор окантовки не всегда можно удачно выбрать и нужно числить большое количество миноров.
--------------------------------------------------
Пример 2.
Задание. Найти ранг матрицы ![]() .
.
![]()

Решение.
1.Переставим четвертый столбец на первое место, а все остальные сместим вправо.
2. Превратим в ноль все элементы в первой строке после ![]() . Для этого к
. Для этого к ![]() столбцам добавим первый умноженный на
столбцам добавим первый умноженный на ![]() соответственно.
соответственно.
3. Третий столбец поделим на ![]() . К четвертого и пятого столбцов добавим третий, умноженный на
. К четвертого и пятого столбцов добавим третий, умноженный на ![]() .
.
4. До пятого столбца добавим четвертый, умноженный на ![]() .
.
5. Переставим третий и четвертый столбцы на второе и третье места, а второй столбец на место четвертого.
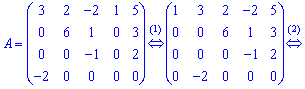
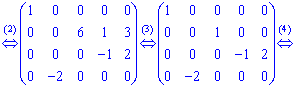
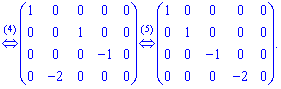
В исходной матрицы вычеркнут последний столбец с нулевыми элементами
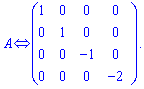
Ранг эквивалентной матрицы равен четырем, а следовательно и ![]() . Можно заметить, что матрицы в первом и втором примерах эквивалентные между собой (имеют одинаковые ранги).
. Можно заметить, что матрицы в первом и втором примерах эквивалентные между собой (имеют одинаковые ранги).
---------------------------------------------------------------
]]>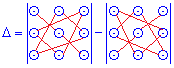
Определители обозначают следующими знаками
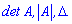
Примеры вычисления определителей
Пример 1. Найти определитель матрицы
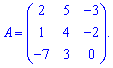
Решение: Применяем правило треугольника для нахождения определителя
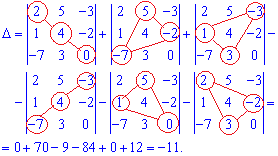
Определитель равен 11.
Приведенная схема пригодиться Вам для вычисления определителя матрицы 3 * 3. Все что Вам нужно - подставить свои значения.
Пример 2. Вычислить определитель матрицы
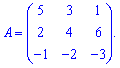
Решение: В целях научить Вас чему-то новому, найдем определитель матрицы по правилу Саррюса.

Схема вычислений приведена выше поэтому копировать ее не будем, а лишь распишем в деталях. Для этого дописываем к стандартному определителю два первых столбца и выполняем следующие расчеты.
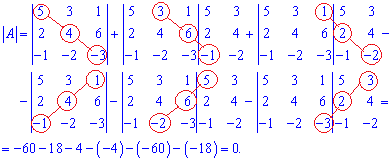
В результате вычислений определитель равен нулю.
Пример 3. Найти определитель матрицы 3*3
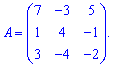 Решение: Применяем правило треугольника для нахождения определителя
Решение: Применяем правило треугольника для нахождения определителя
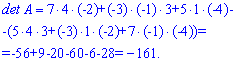
Определитель равен -161.
Пример 4. Вычислить определитель матрицы
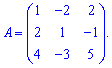
Решение: Находим определитель матрицы 3*3 по правилу треугольников
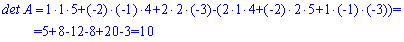
Пример 5. Найти определитель матрицы
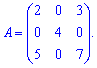
Решение: Матрица имеет несколько нулевых элементов. Такие матрицы называют разреженными. Для уменьшения количества операций вычислим определитель через алгебраические дополнения ко второму строки или столбца.
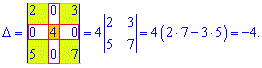
Проще уже не может быть.
Пример 6. Доказать что определитель матрицы А равен 3
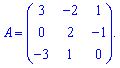
Решение: Матрица содержит два нулевых элементы, поэтому можем найти определитель через алгебраические дополнения. Разложим определитель по элементам первого столбца.
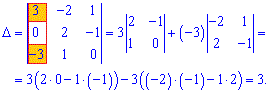
Определитель равен 3 что и требовалось доказать.
Пример 7. Найти определитель матрицы
Решение:По предварительной схеме определитель матрицы вычисляем через алгебраические дополнения первой строки или третьего столбца. выполняем вычисления
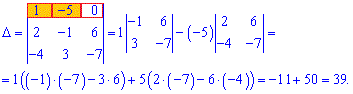
Определитель равен 39.
Пример 8. При каких значениях параметра а определитель матрицы равен нулю
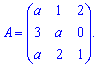
Решение: По правилу треугольников находим определитель
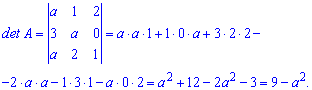
По условию приравниваем определитель к нулю и находим параметр
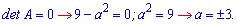
Параметры при которых определитель обращается в нуль уровне a=-3;a=3.
Пример 9. Найти определитель матрицы
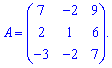
Решение: Найдем определитель матрицы по правилу треугольников и через алгебраические дополнения. По первой схеме получим
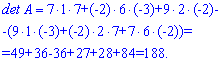
Теперь разложим с помощью алгебраических дополнений, например, третьим столбцом. Он удобен тем, что содержит самые элементы матрицы. Находим определитель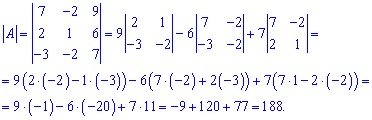
Сравнением количества расчетов убеждаемся, что в таких случаях целесообразнее использовать правило треугольников. Вычисления проще и меньше вероятность сделать ошибку.
Для разреженных матриц или большего порядка блочных стоит применять расписание определителя по строке или столбцу.
И напоследок бонус от нас - калькулятор YukhymCalc.
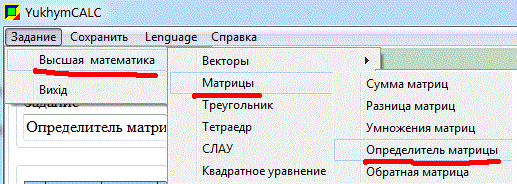
С его помощью Вы легко проверите правильность исчисления основных операций с матрицами, а также сможете найти определитель матрицы и обратную матрицу. Для матриц 3*3 используется правило треугольников, для 4*4 - расписание определителя через элементы первой строки. Меню довольно простое и интуитивно понятное.
Определитель 7 задачу через матричный калькулятор иметь следующий вид

Как видите преимущество матричного калькулятора перед другими, в том числе онлайн калькуляторами, в том, что Вы видите все промежуточные операции. А это важно для проверки и контроля ошибок.
Используйте приведенные схемы вычислений определителей в обучении. Если возникают трудности в вычислениях и есть возможность, то можете проверить найдены определители калькулятором. Скачать матричный калькулятор YukhymCalc Вы можете без регистрации по этой ссылке.
]]>Метод разложения по элементам строк или столбцов
Первый пример мы рассмотрим с подробными объяснениями всех промежуточных действий.
Пример 1. Вычислить определитель методом разложения.

Решение. Для упрощения вычислений разложим определитель четвертого порядка по элементам первой строки (содержит нулевой элемент). Они образуются умножением элементов на соответствующие им дополнения (образуются вычеркивания строк и столбцов на пересечении элемента, для которого исчисляются - выделено красным)
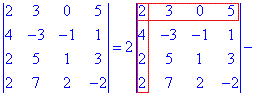
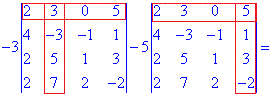
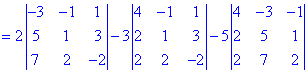
В результате вычисления сведутся к отысканию трех определителей третьего порядка, которые находим по правилу треугольников
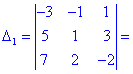
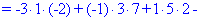
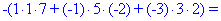
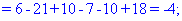
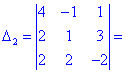
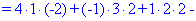
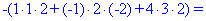
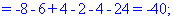
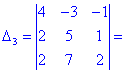
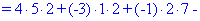
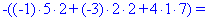
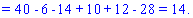
Найденные значения подставляем в выходной детерминант
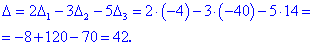
Результат легко проверить с помощью матричного калькулятора YukhymCALC . Для этого в калькуляторе выбираем пункт Матрицы-Определитель матрицы, размер матрицы устанавливаем 4*4.

Далее вводим же матрицу и осуществляем вычисления. Результатом расчетов будет следующий вывод данных

Результаты совпадают, следовательно вычисления проведены верно.
Пример 2. Вычислить определитель матрицы четвертого порядка.

Решение.
Как и в предыдущем задании осуществим вычисления методом разложения. Для этого выберем элементы первого столбца. Упрощенно определитель можно подать через сумму четырех детерминант третьего порядка в виде
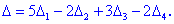
Далее переходим к отысканию определителей по правилу треугольников
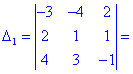
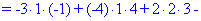
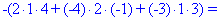
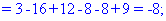
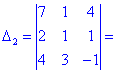
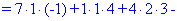
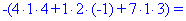
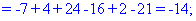
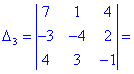
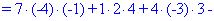
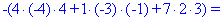
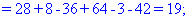
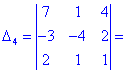
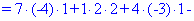
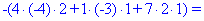
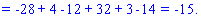
Вычисления не слишком сложные, главное не напутать со знаками и треугольниками. Найденные величины подставляем в главный определитель и суммируем
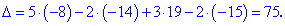
Результат проверяем матричным калькулятором YukhymCALC . Правильность расчетов подтверждается следующим рисунком

Метод возведения определителя к треугольному виду
Данный метод позволяет ряд определителей вычислить достаточно быстрый способ. Суть его заключается в объединении определителя к треугольному виду, при этом следует учитывать все множители на которые увеличиваем или уменьшаем строки и учете при конечных расчетах. Из данного определения Вы ничего для себя не поймете, поэтому лучше все показать на конкретных примерах.
Пример 3. Найти определитель матрицы сведением к треугольному виду
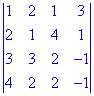
Решение.
Сначала осуществляем математические манипуляции, чтобы получить все нулевые элементы кроме первого в первом столбце. Для этого от второй строки вычитаем первый, умноженный на два. В результате получим
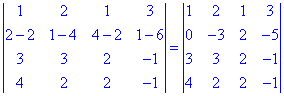
Далее есть два варианта: от третьей строки вычесть первый умноженный на три, или от третьего вычесть сумму первых двух строк. Последний вариант позволит получить сразу два нуля в строке, его и выбираем
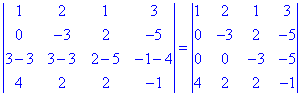
Дальше целесообразнее от четвертой отнять удвоенную вторую строчку. В результате элементарных преобразований определитель примет вид
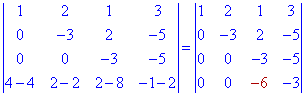
Осталось превратить в ноль один элемент в третьем столбце. Для этого от четвертой строки вычитаем удвоенную третью в предварительно записанном определителе
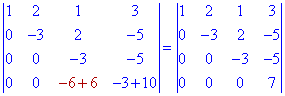
По свойству, определитель треугольной матрицы равен произведению диагональных элементов.
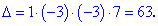
По желанию можно проверить результат матричным калькулятором.

В этом примере никаких умножений строк, в которых зануливали элементы мы не выполняли, поэтому полностью раскрыть метод на этом примере не получилось.
Рассмотрим более сложный.
Пример 4.
Найти определитель матрицы 4-го порядка
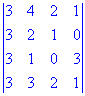
Решение.
Элементарными преобразованиями сводим определитель к треугольного вида. Для этого от каждой строки вычитаем первый. В результате преобразований получим следующий детерминант
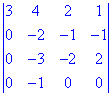
Для удобства вычислений, меняем третью строчку со вторым местами..

По свойству определителей любая замена строк местами ведет к изменению знака определителя. Учитываем это в некотором множителе k=-1.
От третьей строки вычитаем второй, умноженный на минус три. После упрощений получим

Превращаем в ноль последний элемент во втором столбце, для этого вычитаем вторую строчку умноженный на 2.
Результат будет следующим

От удвоенного четвертой строки вычитаем третий. По свойству, умножения строки на постоянную а ведет к изменению определителя в а раз. Данное изменение фиксируем в множителе k=-1*2=-2.

Окончательное значение определителя будет равно произведению диагональных элементов разделенных (или нормированных) на множитель k, который отвечает за изменение детерминанта при элементарных преобразованиях. Выполняем вычисления
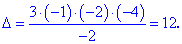
Проверка матричным калькулятором подтверждает правильность производимых вычислений.

Метод разложения определителя по элементам строк или столбцов достаточно быстрым при исчислении определителей больших размеров. Метод сведения к треугольного вида эффективен, если элементарные преобразования легко проследить и не приводят к большим произведений. В других случаях нужно пользоваться комбинацией этих методов, в последнее образовывать как можно больше нулевых элементов, а методом разложения по строкам или столбцам уменьшать количество выполненных операций. Это позволит без проблем вычислять определители третьего, четвертого и даже пятого порядка.
]]>Матрица![]() называется обратной к матрице
называется обратной к матрице![]() ,если выполняются следующие равенства.
,если выполняются следующие равенства.
![]() .
.
Если определитель матрицы![]() отличен от нуля, то матрицу называют не особо или невырожденной.
отличен от нуля, то матрицу называют не особо или невырожденной.
Для того, чтобы матрица имела обратную необходимо и достаточно, чтобы она была невырожденной
Алгоритм нахождения обратной матрицы
Пусть имеем квадратную матрицу
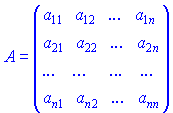
и нужно найти обратную к ней. Для этого нужно выполнить следующие действия:
1. Найти определитель матрицы![]() . Если он не равен нулю то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной
. Если он не равен нулю то выполняем следующие действия. В противном случае данная матрица вырождена и для нее не существует обратной
2. Найти алгебраические дополнения элементов матрицы ![]() . Они равны минорам, умноженным на
. Они равны минорам, умноженным на ![]() в степени суммы строки и столбца, для которого ищем.
в степени суммы строки и столбца, для которого ищем.
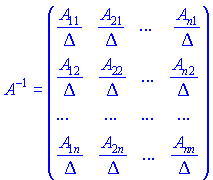
3. Составить матрицу из алгебраических дополнений элементов матрицы ![]() матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается
матрицы и протранспонировать ее. Эта матрица называется присоединенной или союзной и обозначается ![]() .
.
4. Разделить присоединенную матрицу на детерминант ![]() . Полученная матрица будет обратной и иметь свойства, которые изложены в начале статьи.
. Полученная матрица будет обратной и иметь свойства, которые изложены в начале статьи.
--------------------------------------------
Пример 1.
Найти матрицу, обратную к матрице (Дубовик В.П., Юрик И.И. "Высшая математика. Сборник задач")
1) (1.127)
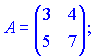
2) (1.130)
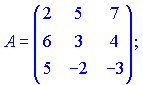
3) (1.133)
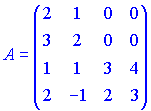
Решение.
1)Находим определитель матрицы
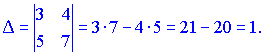
Так как детерминант не равен нулю (![]() ), то обратная матрица существует. Находим матрицу, составленную из алгебраических дополнений
), то обратная матрица существует. Находим матрицу, составленную из алгебраических дополнений
![]()
Матрица дополнений примет вид
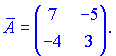
Транспонируем ее и получаем присоединенную ![]()
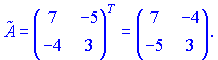
Разделим ее на определитель и получим обратную
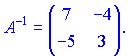
Видим, что в случае, когда определитель равен единице присоединена и обратная матрицы совпадают.
2) Вычисляем определитель матрицы
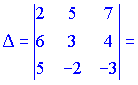
![]()
![]()
Находим матрицу алгебраических дополнений![]()
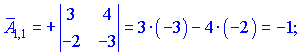
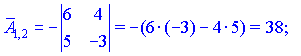
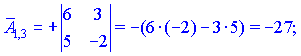
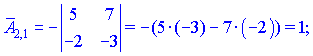
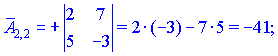
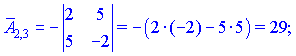
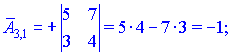
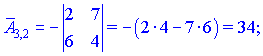
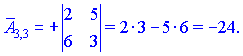
Конечный вид матрицы дополнений
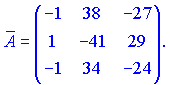
Транспонируем ее и находим союзную матрицу
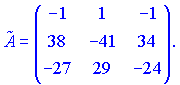
Находим обратную матрицу
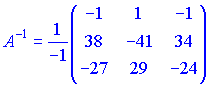
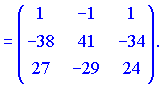
3) Вычислим детерминант матрицы. Для этого разложим его на первую строчку. В результате получим два отличны от нуля слагаемые
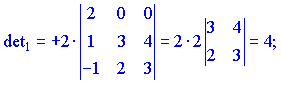
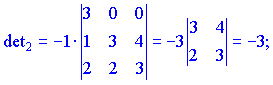
![]()
Находим матрицу алгебраических дополнений![]() . Расписание определителя проводим по строкам и столбцам, в которых больше нулевых элементов (обозначены черным цветом).
. Расписание определителя проводим по строкам и столбцам, в которых больше нулевых элементов (обозначены черным цветом).
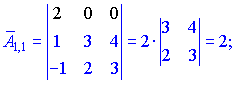
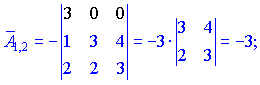
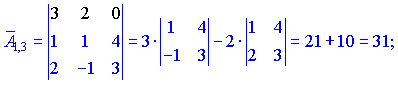
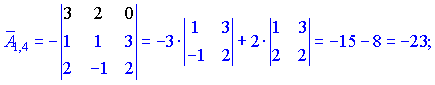
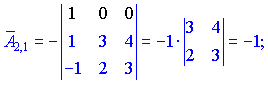
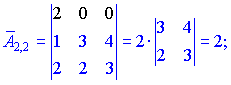
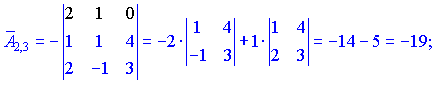
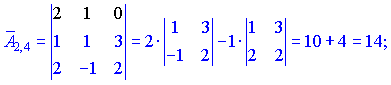
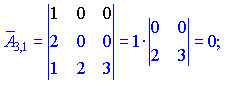
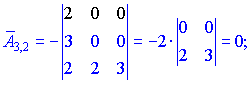
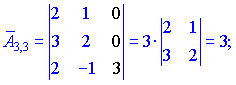
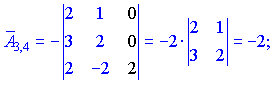
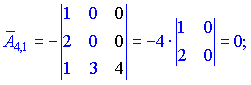
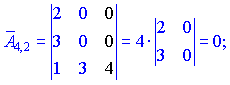
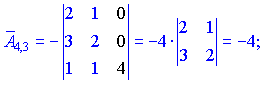
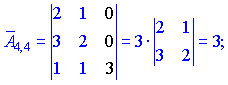
Конечный вид матрицы дополнений следующий
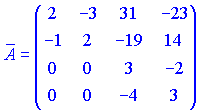
Транспонируем ее и находим присоединенную матрицу
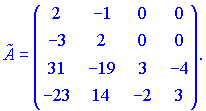
Поскольку определитель матрицы равен единице то обратная матрица совпадает с присоединенной. Данный пример назад.
При вычислениях обратной матрицы типичными являются ошибки связанные с неправильными знаками при вычислении определителя и матрицы дополнений.
--------------------------------------------
------------------------------
]]>- находим определитель главной матрицы;
- дальше вычисляем алгебраические дополнения к матрице;
- последним шагом нужно транспонировать матрицу алгебраических дополнений и разделить на определитель.
Результатом вычислений и будет обратная матрица.
Ниже приведены примеры пошагового вычисления матрицы 3х3.
Пример 1. Найти обратную матрицу
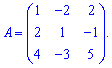
Решение: Вычисляем определитель матрицы 3 * 3 по правилу треугольников
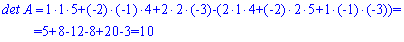
Определитель отличен от нуля, следовательно матрица А не вырожденная и существует обратная к ней.
Алгебраические дополнения равны минорам умноженным на (-1) в степени суммы номера строки и столбца элемента матрицы.
Для простоты можно использовать приведенную ниже схему знаков миноров
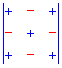
Миноры равны определителю на единицу меньшего порядка чем матрица и образуются вычеркиванием строки и столбца на пересечении которых находится элемент.
Более понятно станет с вычислений алгебраических дополнений
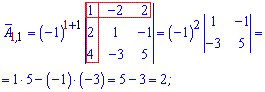
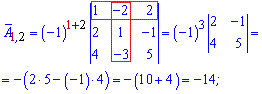
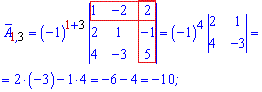
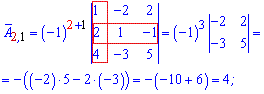
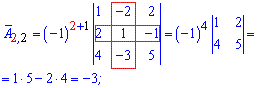
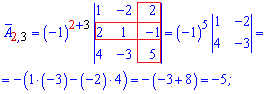
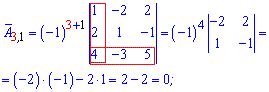
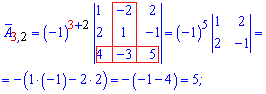
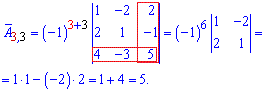
Из найденных значений выписываем матрицу алгебраических дополнений
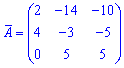
Транспонирует ее чтобы получить присоединенную (союзное) матрицу
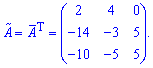
На этом этапе будьте внимательны - можно выполнить правильно приведенные выше вычисления и из-за неумения транспонировать получить неверный результат.
Делим на определитель и получаем обратную матрицу
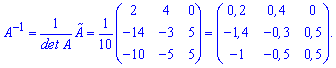
Найти обратную матрицу Вам поможет калькулятор обратной матрицы YukhymCalc. Для этого заходите в меню калькулятора и выбираете вычисления обратных матриц
Далее задаете размер матрицы
и вводить элементы матрицы.
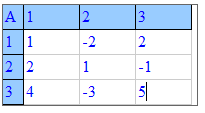
После вычислений Вы получите элементы матрицы дополнений
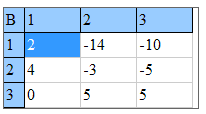
союзной матрицы, и обратной, а также определитель.
Все действия расписаны подробно в отдельном окне

и результаты вычислений можно сохранить в текстовый файл

Используйте калькулятор для нахождения обратной матрицы и проверки правильности вычислений.
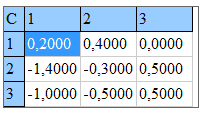
Пример 2. Найти обратную матрицу
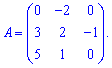
Решение: Вычисляем определитель матрицы разложив его по первой строке. Это довольно удобно так как имеем два элемента которые равны нулю
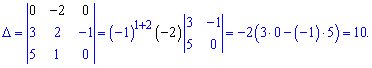
Алгебраические дополнения находим воспользовавшись приведенной выше схемой знаков миноров
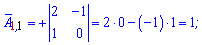
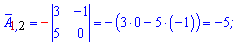
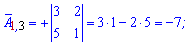
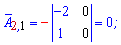
Если в определителе строка или столбец содержит элементы = 0 то он равен 0.
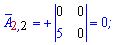
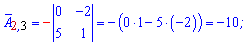
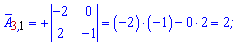
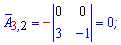
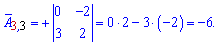
Записываем матрицу алгебраических дополнений
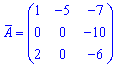
Присоединенную матрицу находим транспонированием найденной
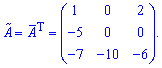
Находим обратную матрицу по известной формуле
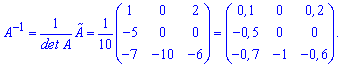
Калькулятор обратной матрицы дает следующий результат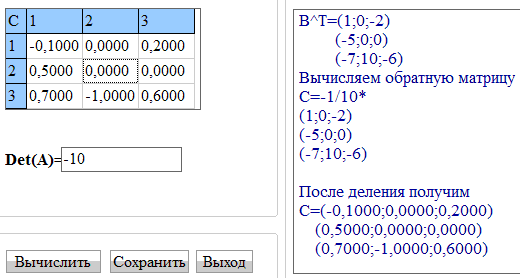
Сравнением убеждаемся что обратную матрицу найдено правильно. Используйте приведенную методику в обучении и с опытом у Вас не будет проблем с обратной матрицей.
]]>Схемы знаков при минорах для детерминантов 3-го - 5-го порядка приведены ниже.
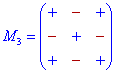
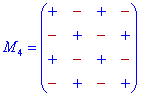
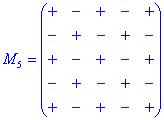
Их не трудно запомнить, если знать следующие правила:
Дополнение к элементам главной диагонали идут со знаком «+», а на параллельных диагоналям чередуются «-», «+», «-», ...
Дополнение к элементам нечетных столбцов и строк начинаются с знака «+», а дальше чередуются «-», «+», для парных начинаются со знака «-», а дальше поочередно меняются «+», «-»,...
Вторым правилом пользуется большинство студентов, поскольку оно привязано к столбца или строки по которому осуществляется расписание определителя.
Перейдем к рассмотрению примеров разложения определителя и изучению особенностей этого метода.
Пример 1.
Разложить определитель третьего порядка по элементам первой строки и второго столбца
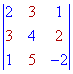
Решение.
Проводим разложение определителя по элементам первой строки
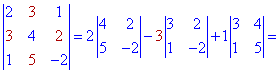
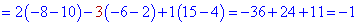
Подобным образом выполняем вычисления разложения по элементам второго столбца
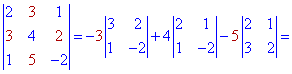
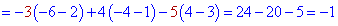
Оба значения одинаковы, а значит расчеты проведены правильно. Если у Вас получится что определители полученные расписанием по строке и столбцу не совпадают - значит где-то допущена ошибка при вычислениях и нужно перечислить или найти ее.
Пример 2.
Найти определитель четвертого порядка методом разложения
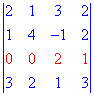
Решение.
Проводим разложение по элементам третьей строки (выделена красным) так как в ней больше всего нулевых элементов.
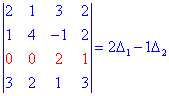
Определители, входящие в расписание находим по правилу треугольников
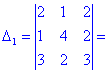
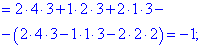
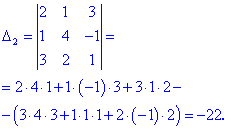
Найденные значения подставляем и посчитываем
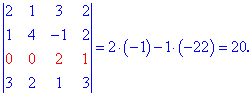
На этом примере метод разложения показал свою эффективность и простоту. Стандартные правила оказались бы слишком громоздкими в вычислениях.
Пример 3.
Найти определитель пятого порядка методом разложения

Решение.
Как и в предыдущем задании ищем строку или столбец содержащие максимальное количество нулевых элементов. Проводим расписание определителя
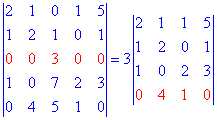
Полученный определитель разложим по четвертой строке
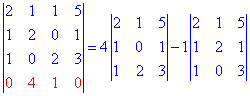
и вычисляем значение
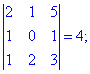
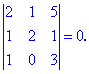
Подставляем в выходной определитель и находим его
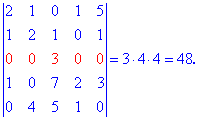
Метод разложения определителя по элементам строк или столбцов является самым быстрым при исчислении определителей больших размеров. Вместо громоздких и сложных вычислений он сводит отыскания определителя к большому количеству простых операций, которые под силу каждому.
]]>