Задача 1. Куб все грани которого закрашены, распилен на 1000 кубиков одинаковых размеров. Определить вероятность того что кубик вытянутый наугад будет иметь:
- а) одну закрашеную грань;
- б) две закрашеные грани.
Вычисления: Если куб распилить на кубики одинакового размера то все грани будут поделены на 100 квадратов. (Примерно как на рисунке)
 Дальше по условию кубик должен иметь одну закрашенную грань - это значит что кубики должны принадлежать внешней поверхности но не лежать на ребрах куба (2 закрашеные поверхности) и не на углах - имеют три закрашеные поверхности.
Дальше по условию кубик должен иметь одну закрашенную грань - это значит что кубики должны принадлежать внешней поверхности но не лежать на ребрах куба (2 закрашеные поверхности) и не на углах - имеют три закрашеные поверхности.
Следовательно, искомое количество равно произведению 6 граней на количество кубиков в квадрате размером 8*8.
6*8*8=384 – кубики с 1 закрашеной поверхностью.
Вероятность равна количеству благоприятных событий к общему их количеству P=384/1000=0,384.
б) Две закрашеные грани имеют кубики по ребрам без самих вершин куба. На одном ребре будет 8 таких кубиков. Всего в кубе 12 ребер, поэтому две закрашенные грани имеют
8*12=96 кубиков.
А вероятность вытянуть их среди 1000 всех равная
P=96/1000=0,096.
На этом задание решено и переходим к следующему.
Задача 2. На одинаковых карточках написаны буквы А, А, А, Н, Н, С. Какова вероятность того, что случайно разместив карточки в ряд, получим слово АНАНАС?
Вычисления: Нужно рассуждать всегда от того, что известно. Дано 3 буквы А, 2-Н, и 1 - С, всего их 6. Начнем выбирать буквы для слова "ананас". Первой идет буква А, которую мы можем выбрать 3 способами из 6, потому что есть 3 буквы А среди 6 известных. Поэтому вероятность вытянуть первой А равна
P1=3/6=1/2.
Вторая буква Н, но не следует забывать, что после того как вытащили А остается 5 букв для выбора. Поэтому вероятность вытянуть под 2 номером Н равна
P2=2/5.
Следующую А вероятность вытянуть среди 4, что осталось
P3=2/4.
Далее Н можно извлечь из вероятностью
P4=1/3.
Чем ближе к концу тем больше вероятность, и уже А можем извлечь при
P5=1/2.
После этого остается одна карточка С, поэтому вероятность ее вытащить равна 100 процентам или
P6=1.
Вероятность составить слово АНАНАС равна произведению вероятностей
P=3/6*2/5*2/4*1/3*1/2*1=1/60=0,016(6).
На этом и базируются подобные задачи по теории вероятностей.
Задача 3. Из партии изделий товаровед наугад выбирает образцы. Вероятность того что наугад взятое изделие окажется высшего сорта равна 0,8. Найти вероятность того, что среди 3 отобранных изделий будет два изделия высшего сорта?
Вычисления: Данный пример на применение формулы Бернулли.
p=0,8; q=1-0,8=0,2.
Вероятность вычисляем по формуле
![]()
Если объяснять не на языке формул, то нужно составить комбинации из трех событий, два из которых благоприятны, а одно нет. Это можно записать суммой произведений
![]()
Оба варианта являются равносильными, только первый можем применить во всех задачах, а второй в подобных к рассмотреной.
Задача 4. Из пяти стрелков двое попадают в цель с вероятностью 0,6 и трое с вероятностью 0,4. Что вероятнее: наугад выбранный стрелок попадает в цель или нет?
Вычисления: По формуле полной вероятности определяем вероятность, что стрелок попадет.
P=2/5*0,6+3/5*0,4=0,24+0,24=0,48.
Вероятность меньше P<0,5, следовательно вероятнее что наугад выбранный стрелок не попадет в цель.
Вероятность не попадания составляет
![]()
или
P=2/5*(1-0,6)+3/5*(1-0,4)=0,16+0,36=0,52.
Задача 5. C 20 студентов, пришедших на экзамен, 10 подготовлены отлично (знают все вопросы), 7 хорошо (знают по 35 вопросов), а 3 плохо (10 вопросов). В программе 40 вопросов. Наугад вызванный студент ответил на три вопроса билета. Какова вероятность того, что он подготовлен на
- а) отлично;
- б) плохо.
Вычисления: Суть задачи заключается в том что студент ответил на три вопроса билета, то есть на все что были заданы, а вот какова вероятность их вытянуть мы сейчас вычислим.
Найдем вероятность что студент ответил на три вопроса правильно. Это будет отношение количества студентов ко всей группе умноженное на вероятность вытянуть билеты которые они знают среди всех возможных
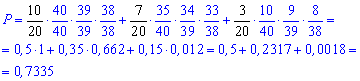
Теперь найдем вероятность что студент принадлежит группе которая подготовлена "на отлично". Это равносильно доле первого слагаемого предварительной вероятности, к самой вероятности
![]()
Вероятность, что студент принадлежит группе которая плохо подготовилась достаточно мала и равна 0,00216.
![]()
На этом задание выполнено. Хорошо его разберите и запомните как вычислять, поскольку на контрольных и тестах оно распространено.
Задача 6. Монету бросают 5 раз. Найти вероятность того что герб выпадет менее 3 раз?
Вычисления: Вероятность вытянуть герб или решку равносильна и равна 0,5. Менее 3 раз означает, что герб может выпасть либо 0, либо 1, либо 2 раза. "Или" всегда в вероятности в операциях сказывается добавлением.
Вероятности находим по формуле Бернулли
![]()
Поскольку p=q=0,5, то вероятность равна
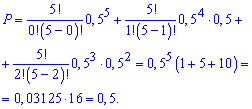
Вероятность равна 0,5.
Задача 7. При штамповке металлических клемм получается в среднем 90% стандартных. Найти вероятность того что среди 900 клемм стандартными будут не менее 790 и не более 820 клемм.
Вычисления: Вычисления необходимо проводить по интегральной теореме Муавра-Лапласа.
Записываем известные величины
n=900; p=0,9; q=1-0,9=0,1; k1=790; k2=820.
Вероятность находим по формуле
![]()
где ![]() интегральная функция Лапласа
интегральная функция Лапласа
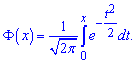
Значение x1, x2 вычисляем по формуле
![]()
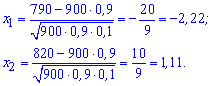
Далее находим вероятность что среди 900 клемм стандартными будут не менее 790 и не более 820
![]()
Если объясните подобные задачи так как здесь написано то за контрольную по вероятности получите оценку "отлично".
Индивидуальное задание 1
Вариант 8
Задача 1. Составить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моде;
- квантильное отклонения;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Выборка задана следующими значениями
4, 9, 7, 4, 7, 5, 6, 3, 4, 5, 7, 2, 3, 8, 5, 6, 7, 4, 3, 4.
Решение: Записываем выборку в виде вариационного ряда (в порядке возрастания):
2; 3; 3; 3; 4; 4; 4; 4; 4; 5; 5; 5; 6; 6; 7; 7; 7; 7; 8; 9.
Запишем статистическое распределение выборки в виде дискретного статистического распределения частот:
![]()
Значение эмпирической функции распределения определяем по формуле
![]()
где nx количество элементов выборки меньше х. Используя таблицу, а также учитывая, что объем выборки n=1+3+5+3+2+4+1+1=20, запишем эмпирическую функцию распределения:
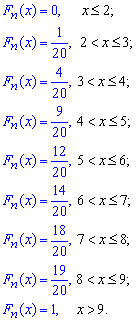
Далее вычислим числовые характеристики статистического распределения выборки.
1. Выборочное среднее вычисляем по формуле
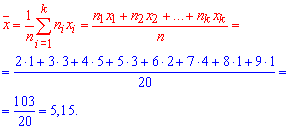
2. Выборочную дисперсию вычисляем по формуле
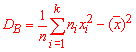
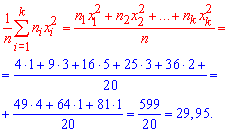
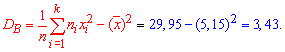
3. Подправленную дисперсию находим по формуле
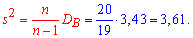
4. Выборочное среднее квадратичное отклонение вычисляем по формуле
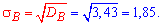
5. Подправленное среднее квадратичное отклонение находим по формуле
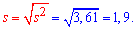
6. Размах выборки вычисляем как разность между наибольшим и наименьшим значениями вариант, то есть:
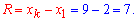
7. Медиану вычисляют по формулам:
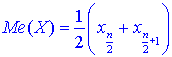 если число n - четное;
если число n - четное;
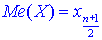 если число n - нечетное.
если число n - нечетное.
Здесь берем индексы в x[i] согласно нумерации вариант в вариационном ряду.
В нашем случае п=20, поэтому
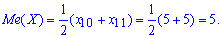
8. Мода - это варианта которая в вариационном ряду случается чаще всего, то есть
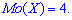
9. Квантильное отклонение найдем по формуле
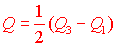
половины разницы 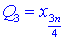 – третьего и
– третьего и 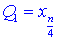 – первого квантилей.
– первого квантилей.
Сами же квантили получаем искусственной разбивкой вариационного ряда на 4 равные части. В нашем случае
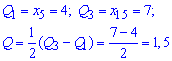
10. Коэффициент вариации вычисляем по формуле
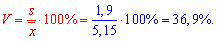
11. Коэффициент асимметрии находим по формуле
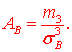
Здесь m3 центральный эмпирический момент 3-го порядка,
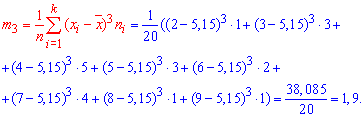
Отсюда коэффициент асимметрии равен 0,3
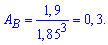
12. Эксцессом 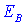 статистического распределения выборки называется число которое находят по формуле:
статистического распределения выборки называется число которое находят по формуле:
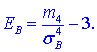
В числителе имеем 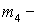 центральный эмпирический момент 4-го порядка
центральный эмпирический момент 4-го порядка
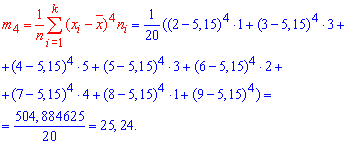
Момент и среднее квадратичное отклонение подставляем в формулу и определяем эксцесс
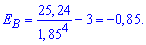
По тому как все доступно и понятно на практике выглядит делаем вывод, что найти моду, медиану и дисперсию должен уметь каждый студент, который изучает теорию вероятностей.
Готовые решения по теории вероятностей
- Следующая статья - Определение уравнения прямой регрессии и интервала доверия
Вариант-8
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:

Записать выборочное уравнение прямой регрессии Y на X.
Решение: Для построения прямой регрессии Y на X следует сначала найти среднее значение каждой из признаков:
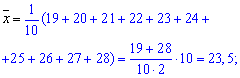
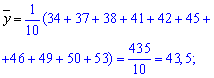
Далее сумму их попарных произведений
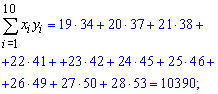
и квадратов значений признака X
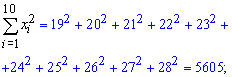
После этого можем посчитать сами коэффициенты, фигурирующие в уравнении прямой регрессии
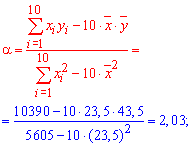
Ну и самая легкая часть - это все подставить в уравнение регрессии y=2,02*x-4,205.С виду формул видим что чрезвычайно сложных операций выполнять здесь не приходится. Однако и здесь многие из Вас умудряются наделать ошибок.
Для подтверждения линейной связи между признаками Y на X следует еще найти выборочный коэффициент корреляции:
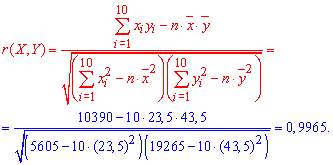
Чем он ближе к единице, тем лучше линейная функция описывает зависимость между признаками. В нашем случае выборочный коэффициент корреляции r(X, Y) практически совпадает с единицей, поэтому делаем вывод что предположение о линейности связи между X и Y правильное. Также коэффициент корреляции больше нуля r>0, что свидетельствует о положительный связь между X и Y, то есть эти случайные величины увеличиваются одновременно.
Задача 2. Найти интервал доверия a для оценки с надежностью γ неизвестного математического ожидания нормально распределенного признака Х генеральной совокупности:
- а) если γ=0,96, генеральная среднее квадратичное отклонение σ=5,0, выборочное среднее
 =28,0, а объем выборки n=25;
=28,0, а объем выборки n=25; - б) если γ=0,99, подправленное среднее квадратичное отклонение s=12,0, выборочное среднее
 =65,0, а объем выборки n=16.
=65,0, а объем выборки n=16.
Решение: а) Из уравнения ![]() с помощью функции Лапласа методом интерполяции из соседних значений находим t
с помощью функции Лапласа методом интерполяции из соседних значений находим t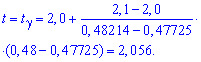
Границы интервала доверия находим с формулами:
![]()
![]()
Записываем интервал доверия ![]() с надежностью 0,96.
с надежностью 0,96.
б) Поскольку n=16<30 и среднее квадратичное отклонение  неизвестно, то для нахождения границ интервала доверия используем формулу
неизвестно, то для нахождения границ интервала доверия используем формулу
![]()
где значение 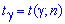 ищем с помощью таблиц (распределение Стьюдента):
ищем с помощью таблиц (распределение Стьюдента):
![]()
![]()
![]()
Итак, интервал доверия равный ![]() с надежностью 0,99.
с надежностью 0,99.
Задача 3. Найти интервал доверия для оценки с надежностью γ=0,99 неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 35, а подправленное среднее квадратичное отклонение s=10,3.
Решение: Задача сводится к отысканию интервала доверия 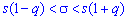 который покрывает
который покрывает  с заданной надежностью
с заданной надежностью 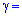 0,99.
0,99.
По таблице функции q находим
![]()
Искомый интервал доверия лежит в пределах
![]()
или
![]()
Дочитайте ответы до конца и теория вероятности станет для Вас на шаг понятней и доступней.
Готовые решения по теории вероятностей
- Предыдущая статья - Найти моду, медиану, дисперсию может каждый!
- Следующая статья - Методика проверки гипотез на нормальное распределение
Вариант - 8
Задача 1. В таблице приведены эмпирические частоты
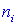 и теоретические частоты
и теоретические частоты 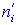 рассчитанные исходя из гипотезы H0 о нормальном распределении генеральной совокупности. Для уровня значимости
рассчитанные исходя из гипотезы H0 о нормальном распределении генеральной совокупности. Для уровня значимости 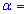 0,01 проверить гипотезу H0 о нормальном распределении генеральной совокупности.
0,01 проверить гипотезу H0 о нормальном распределении генеральной совокупности.
Решение: Вычисляем эмпирическое значение критерия Пирсона (m=5)
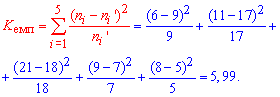
По таблице критических точек распределения хи-квадрат
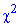 для уровня значимости
для уровня значимости 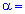 0,01 и числа степеней свободы k=m-r-1=5-2-1=2 (r=2 для нормального распределения) находим критическое значение:
0,01 и числа степеней свободы k=m-r-1=5-2-1=2 (r=2 для нормального распределения) находим критическое значение: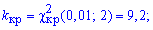
Итак эмпирическое значение меньше критического
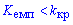 следовательно гипотезу H0 принимаем.
следовательно гипотезу H0 принимаем.
Задача 2. Для нормально распределенной генеральной совокупности с известным средним отклонениям 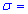 0,5 получено выборку объемом n=64 и за ней найдено выборочное среднее
0,5 получено выборку объемом n=64 и за ней найдено выборочное среднее 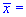 77,88. Для уровня значимости
77,88. Для уровня значимости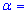 0,05 проверить гипотезу
0,05 проверить гипотезу 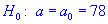 при наличии альтернативной гипотезы.
при наличии альтернативной гипотезы. 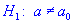 .
.
Решение: Вычислим эмпирическое значение критерия:
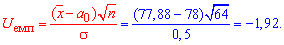
Для альтернативной гипотезы H1: 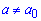 находим критическое значение
находим критическое значение 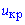 по таблице значений функции Лапласа, используя формулы интерполяции
по таблице значений функции Лапласа, используя формулы интерполяции
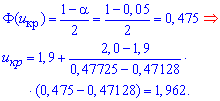
Поскольку эмпирическое значение меньше эмпирическое значение меньше критичного 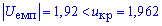 , то гипотезу H0 принимаем.
, то гипотезу H0 принимаем.
Задача 3. Для выборки объемом n=16 нормально распределенной генеральной совокупности найдено выборочное среднее 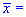 89,7 и подправленное среднее квадратичное отклонение s=1,0. Для уровня значимости
89,7 и подправленное среднее квадратичное отклонение s=1,0. Для уровня значимости 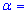 0,025 проверить гипотезу H0: a=a0=89 при наличии альтернативной гипотезы. H1: a>a0.
0,025 проверить гипотезу H0: a=a0=89 при наличии альтернативной гипотезы. H1: a>a0.
Решение: Находим эмпирическое значение критерия:
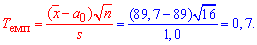
По таблице критических точек распределения Стьюдента для заданного уровня значимости 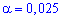 (для односторонней критической области) и количества степеней свободы k=16-1=15 находим критическую точку
(для односторонней критической области) и количества степеней свободы k=16-1=15 находим критическую точку
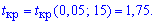
Поскольку эмпирическое значение меньше критического 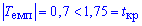 , то гипотезу H0 принимаем.
, то гипотезу H0 принимаем.
Задача 4. Для выборки объемом n=21 нормально распределенной генеральной совокупности найдено подправленную дисперсию 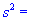 13,3. Для уровня значимости 0,1 проверить гипотезу
13,3. Для уровня значимости 0,1 проверить гипотезу 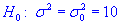 при наличии альтернативной гипотезы.
при наличии альтернативной гипотезы. 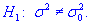
Решение: Находим эмпирическое значение критерия:
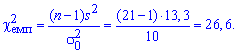
С помощью таблицы критических точек распределения 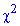 определяем «левую» критическую точку
определяем «левую» критическую точку
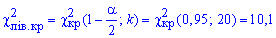
и «правую» критическую точку
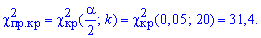
Поскольку условие выполняется 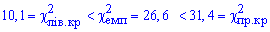 , то гипотезу H1 принимаем.
, то гипотезу H1 принимаем.
Задача 5.Для выборки объемом n=15 нормально распределенной генеральной совокупности найдено подправленную дисперсию 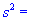 6,3. Для уровня значимости
6,3. Для уровня значимости 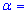 0,025 проверить гипотезу
0,025 проверить гипотезу 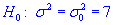 при наличии альтернативной гипотезы.
при наличии альтернативной гипотезы. 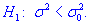
Решение: Вычисляем эмпирическое значение критерия:
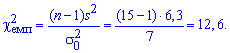
С помощью таблицы критических точек распределения "хи-квадрат"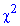 определяем
определяем
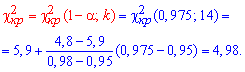
Поскольку условие 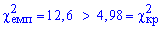 имеет место, то гипотезу H0 принимаем.
имеет место, то гипотезу H0 принимаем.
Если на контрольной или тестах выполните проверку гипотез подобно приведенной методике, то к теории вероятностей у преподавателей к Вам точно не будет претензий. Для всех остальных случаях обращайтесь за помощью к нам!
Готовые решения по теории вероятностей
]]>Вариант 13. Индивидуальное задание 1.
Задача 1. Построить статистическое распределение выборки, записать эмпирическую функцию распределения и вычислить такие числовые характеристики:
- выборочное среднее;
- выборочную дисперсию;
- подправленную дисперсию;
- выборочное среднее квадратичное отклонение;
- подправленное среднее квадратичное отклонение;
- размах выборки;
- медиану;
- моде;
- квантильне отклонения;
- коэффициент вариации;
- коэффициент асимметрии;
- эксцесс для выборки:
Задача сформированы в виде таблицы (далее - по вариантам, № варианта = № студента в списке группы)
7, 6, 5, 8, 6, 5, 6, 9, 8, 7, 10, 5, 4, 9, 7, 9, 6, 9, 11, 6.
Решение: Запишем выборку в виде вариационного ряда (в порядке возрастания):
4; 5; 5; 5; 6; 6; 6; 6; 6; 7; 7; 7; 8; 8; 9; 9; 9; 9; 10; 11.
Запишем статистическое распределение выборки в виде дискретного статистического распределения частот:
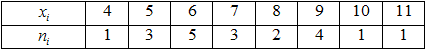 Эмпирическую функцию распределения определять по формуле
Эмпирическую функцию распределения определять по формуле
![]()
где nx количество элементов выборки которые меньше х.
Используя таблицу и учитывая что объем выборки равен
![]()
запишем эмпирическую функцию распределения:
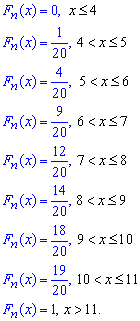


Далее вычисляем числовые характеристики статистического распределения выборки.
1) выборочное среднее находим по формуле
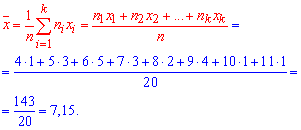
2) выборочную дисперсия вычисляем по формуле
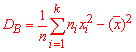
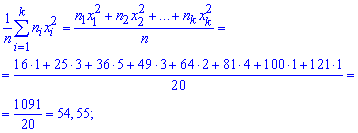
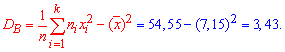
3) подправленную дисперсию находим по формуле
![]()
4) выборочное среднее квадратичное отклонение вычисляем по формуле
![]()
5) подправленное среднее квадратичное отклонение находим по формуле
![]()
6) Размах выборки вычисляем как разность между наибольшим и наименьшим значениями ее вариантов, а именно:
![]()
7) Медиану вычисляют согласно формулам:
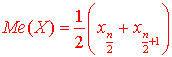
если число n - четное;
![]()
если число п - нечетное.
Здесь берем индексы xi в соответствии с нумерацией вариант в вариационном ряду.
В нашем случае п=20, поэтому
![]()
8) Мода - это варианта которая в вариационном ряду случается чаще всего, то есть ![]()
9) Квантильное отклонение вычисляют по формуле
![]()
где ![]() – первый квантиль,
– первый квантиль, ![]() – третий квантиль.
– третий квантиль.
Квантили получаем мнимым разбитием вариационного ряда на 4 равные части.
В нашем случае
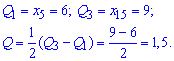

10) Коэффициент вариации находим по формуле
![]()
11) Коэффициент асимметрии вычисляем по формуле
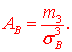
В числителе ![]() центральный эмпирический момент 3-го порядка, который находим по формуле
центральный эмпирический момент 3-го порядка, который находим по формуле
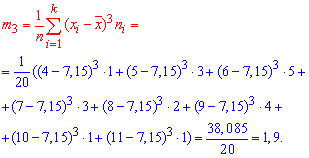
Таким образом коэффициент асимметрии равен 0,3
![]()
12) Эксцессом ![]() статистического распределения выборки называется число, которое вычисляется по формуле:
статистического распределения выборки называется число, которое вычисляется по формуле:
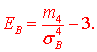
Здесь ![]() центральный эмпирический момент 4-го порядка
центральный эмпирический момент 4-го порядка
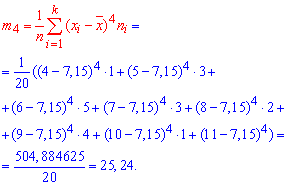
![]()
Итак, получим отрицательный эксцесс EB=-0,85.
На этом индивидуальное задание №1 решено. Из него вы научились находить числовые характеристики дискретного распределения.
Готовые решения по теории вероятностей
- Следующая статья - Уравнение прямой регрессии Y на X. Интервал доверия
Вариант 13. Индивидуальное задание 2.
Задача 1. Связь между признаками Х и Y генеральной совокупности задается таблицей:
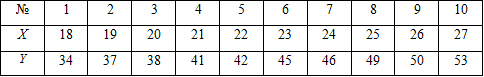
Записать выборочное уравнение прямой регрессии Y на X.
Решение: Вычисляем согласно формул вероятности нужные величины для составления выборочного уравнения регрессии:
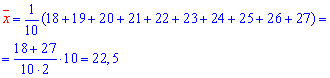
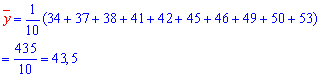
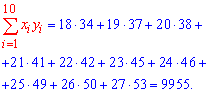
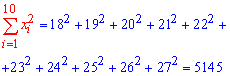
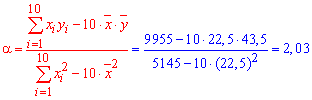
Итак, выборочное уравнение регрессии y=alpha*x+beta
y=2,03*x-2,175.
Вычислим выборочный коэффициент корреляции:
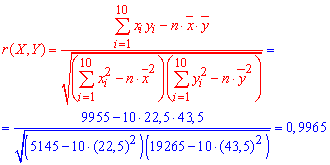
Поскольку выборочный коэффициент корреляции
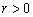 , поэтому связь между Х и У положительная и эти случайные величины увеличиваются одновременно.
, поэтому связь между Х и У положительная и эти случайные величины увеличиваются одновременно.
Задача 2. Найти интервал доверия а для оценки с надежностью ![]() неизвестного математического ожидания нормально распределенного признака Х генеральной совокупности:
неизвестного математического ожидания нормально распределенного признака Х генеральной совокупности:
а) если ![]() =0,96, генеральная среднее квадратичное отклонение
=0,96, генеральная среднее квадратичное отклонение ![]() =5,0, выборочное среднее
=5,0, выборочное среднее ![]() =21,0, а объем выборки n=36;
=21,0, а объем выборки n=36;
б) если ![]() =0,99, подправленное среднее квадратичное отклонение s=6,0, выборочное среднее
=0,99, подправленное среднее квадратичное отклонение s=6,0, выборочное среднее ![]() =45,0, а объем выборки n=9.
=45,0, а объем выборки n=9.
Решение: а) Из уравнения на функцию Лапласа ![]() с помощью таблицы методом интерполяции находим t
с помощью таблицы методом интерполяции находим t
![]()
Границы интервала доверия ищем по формулам:
![]()
![]()
Интервал доверия равный ![]() с надежностью
с надежностью ![]() =0,96.
=0,96.
б) Поскольку объем выборки меньше 30 (n=9<30) и среднее квадратичное отклонение ![]() неизвестно, то для нахождения границ интервала доверия используем формулу
неизвестно, то для нахождения границ интервала доверия используем формулу
![]()
где значение![]() ищем с помощью таблиц (распределение Стьюдента):
ищем с помощью таблиц (распределение Стьюдента):
![]()
![]()
![]()
После вычислений интервал доверия равный ![]() с надежностью 0,99.
с надежностью 0,99.
Задача 3. Найти интервал доверия для оценки с надежностью ![]() =0,95неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 11, а подправленное среднее квадратичное отклонение s=9,3.
=0,95неизвестного среднего квадратичного отклонения σ нормально распределенного признака Х генеральной совокупности, если объем выборки n = 11, а подправленное среднее квадратичное отклонение s=9,3.
Решение: Задача сводится к отысканию интервала доверия ![]() который покрывает
который покрывает ![]() с заданной надежностью
с заданной надежностью ![]() =0,95.
=0,95.
По таблице находим ![]()
Искомый интервал доверия занимает область ![]() или
или
![]()
Как видите вычисления под силу каждому, главное уметь пользоваться формулами и таблицами (распределение Стьюдента). Проверка гипотез на нормальное распределение будет рассмотрена в следующей статье.
Готовые решения по теории вероятностей
- Предыдущая статья - Числовые характеристики статистического распределения
- Следующая статья - Проверка гипотезы о нормальном распределении
Вариант 13. Индивидуальное задание 3
Задача 1. В таблице приведены эмпирические частоты ni и теоретические частоты
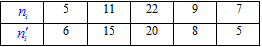
Решение: Вычислим эмпирическое значение критерия Пирсона (![]() )
)
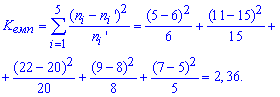
По таблице критических точек распределения "хи-квадрат" ![]() для уровня значимости
для уровня значимости ![]() и числа степеней свободы 2
и числа степеней свободы 2
![]() (r=2 для нормального распределения) находим критическое значение
(r=2 для нормального распределения) находим критическое значение
![]()
Поскольку эмпирическое значение меньше критического ![]() то гипотезу H0 принимаем.
то гипотезу H0 принимаем.
Задача 2. Для нормально распределенной генеральной совокупности с известным средним отклонениям ![]() =2,0 получено выборку объемом n=64 и за ней найдено выборочное среднее
=2,0 получено выборку объемом n=64 и за ней найдено выборочное среднее ![]() =94,4. Для уровня значимости
=94,4. Для уровня значимости ![]() =0,01 проверить гипотезу H0: a=a0=95 при наличии альтернативной гипотезы H1: a<a0.
=0,01 проверить гипотезу H0: a=a0=95 при наличии альтернативной гипотезы H1: a<a0.
Решение: Находим эмпирическое значение критерия:
![]()
Для альтернативной гипотезы H1: a<a0 находим критическое значение ![]() по таблице значений функции Лапласа, используя формулы интерполяции
по таблице значений функции Лапласа, используя формулы интерполяции
![]()
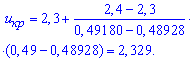
Поскольку эмпирическое значение U меньше критического u
![]()
то гипотезу H0 отклоняем и принимаем гипотезу H1 .
Задача 3. По выборке объемом n=25 для нормально распределенной генеральной совокупности найдено выборочное среднее ![]() =94,4 и подправленное среднее квадратичное отклонение s=2,0. Для уровня значимости
=94,4 и подправленное среднее квадратичное отклонение s=2,0. Для уровня значимости ![]() =0,05 проверить гипотезу H0: a=a0=95 при наличии альтернативной гипотезы H1: a<>a0..
=0,05 проверить гипотезу H0: a=a0=95 при наличии альтернативной гипотезы H1: a<>a0..
Решение: Вычислим эмпирическое значение критерия:
![]()
Находим по таблице критических точек распределения Стьюдента для заданного уровню значимости ![]() (для двусторонней критической области) и количеством степеней свободы k=25-1=24 критическую точку
(для двусторонней критической области) и количеством степеней свободы k=25-1=24 критическую точку
![]()
Поскольку условие вхождения выполняется ![]() , то гипотезу H0принимаем.
, то гипотезу H0принимаем.
Задача 4. По выборке объемом n = 17 для нормально распределенной генеральной совокупности найдено подправленную дисперсию ![]() =4,8. Для уровня значимости
=4,8. Для уровня значимости ![]() =0,02 проверить гипотезу
=0,02 проверить гипотезу ![]() при наличии альтернативной гипотезы.
при наличии альтернативной гипотезы.![]()
Решение: Находим эмпирическое значение критерия:
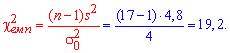
С помощью таблицы критических точек распределения "хи -квадрат" ![]() определяем "левую" критическую точку
определяем "левую" критическую точку
![]()
и "правую" критическую точку
![]()
Поскольку эмпирическое значение критерия принадлежит интервалу критических точек распределения![]() то гипотезу H1 принимаем.
то гипотезу H1 принимаем.
Задача 5. По выборке объемом n = 19 для нормально распределенной генеральной совокупности найдено подправленную дисперсию ![]() =4,3. Для уровня значимости
=4,3. Для уровня значимости ![]() =0,01 проверить гипотезу
=0,01 проверить гипотезу ![]() при наличии альтернативной гипотезы
при наличии альтернативной гипотезы![]()
Решение: Вычислим эмпирическое значение критерия Хи-квадрат:
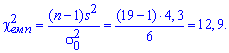
С помощью таблицы критических точек распределения "хи -квадрат" ![]() определяем
определяем
![]()
Поскольку ![]() , то гипотезу H0 принимаем.
, то гипотезу H0 принимаем.
На этом одно из индивидуальных заданий решено и обоснованно. Формул с вероятности Вы изучили немало, как проверить гипотезы знаете из приведенных примеров. Большее готовых решений по теории вероятностей Вы найдете в категории "Контрольные по вероятности". Также всегда можете заказать контрольную по вероятности у нас, как Вы убедились такие задачи Нам под силу!
Готовые решения по теории вероятностей
]]>