Как найти площадь плоской фигуры, которая ограничена кривыми?

Разберем готовые ответы к примерам на нахождение площади плоской фигуры, которая ограничена кривыми через двойные интегралы.
Задание не сложные, а вся схема нахождения площади требует всего трех вещей:
знание элементарных функций и умение искать точки их пересечения;
понимание как через криволинейные интегралы искать площадь, умение правильно расставлять пределы;
хорошых знаний теории вычисления интегралов, поскольку к этому все сводится.

ЗАДАНИЕ 4.1 Найти площадь плоской фигуры, которая образована линиями:
x=4-y², x+2y=4.
Решение: Фигура ограничена x=4-y² - параболой с вершиной в точке O(4;0) и ветками влево;
но x+2y=4 - прямой, которая отрезается на осях в точках (4;0) и (0;2).
Найдем точки пересечения графиков функций из системы уравнений:

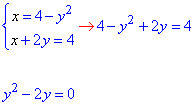
При ее решении получим две точки

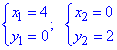
График параболы и прямой приведен на рисунку

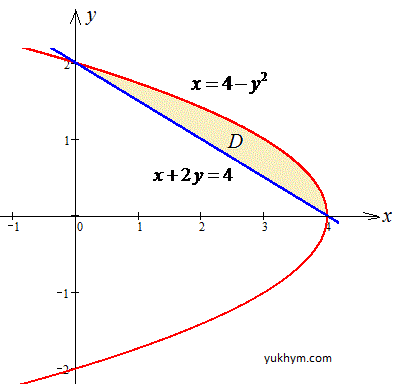
Запишем пределы интегрирования:
D: 0≤x≤4,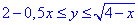
Здесь имеем y=√(4-x) - уравнение верхней части параболы x=4-y^2;
Вычислим площадь фигуры нахождением двойного интеграла:

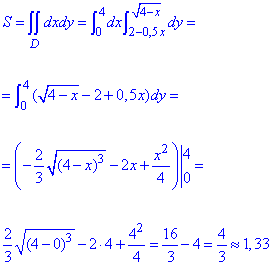
Площадь равна 1,33 единиц квадратных.

ЗАДАНИЕ 4.2 Найти площадь плоской фигуры, которая образована кривыми:
y=2-x, y²=4x+4.
Решение: y^2=4x+4 - парабола с вершиной в точке O (-1;0) и ветками вправо;
y=2-x, x+y=2 - прямая, которая отрезается на осях в точках (2;0) и (0;2).
Складываем систему уравнений для нахождения точек пересечения графиков заданных кривых:

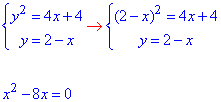
При решении получим две точки

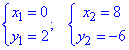
График области интегрирования имеет вид

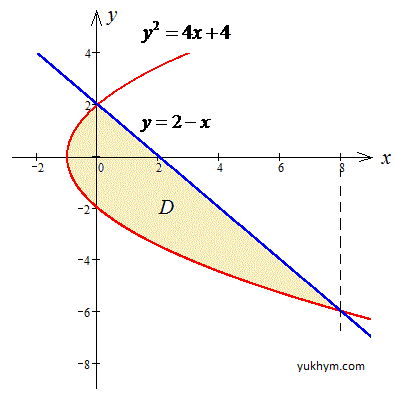
Пределы в области D:
-6≤x≤2, 0,25y²-1≤y≤2-y.
Находим площадь фигуры через криволинейный интеграл:

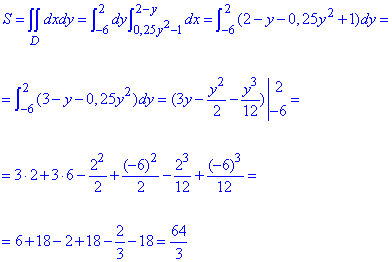
Кратный интеграл не трудно интегрировать.

ЗАДАНИЕ 4.3 Найти площадь плоской фигуры, которая образована линиями:
x²+y²=4, x²+y²=4x.
Решение: Область интегрирования ограничена x²+y²=4 - кругом с центром в точке O₁(0;0) и радиусом R=2;
x²+y²=4x, x²-4x+4+y²=4, (x-2)²+y²=2² - круг с центром в точке O₁(2;0) и радиусом R=2.
Найдем точки пересечения графиков заданных функций из системы уравнений:

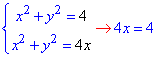
отсюда

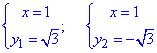
График фигуры, площадь которой ищем приведен на рисунку 

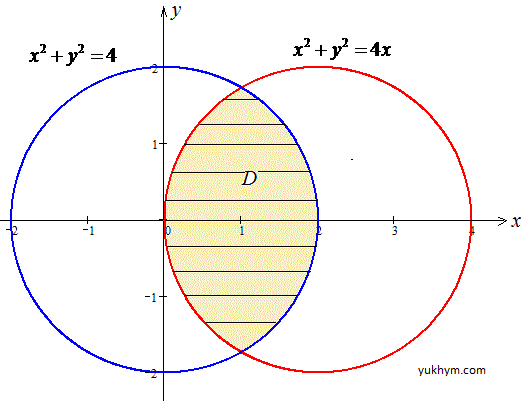
Расставим пределы в области D
(поскольку область симметрична относительно прямой y=0, то будем рассматривать ее половину, а результат умножим на 2):
D: 0≤y≤√3,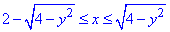
Здесь записали:
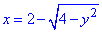- уравнение левого полукруга (x-2)²+y²=4;
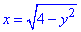- уравнение правого полукруга x²+y²=4.
Вычислим площадь фигуры через двойной интеграл:

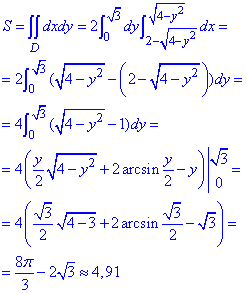
При интегрировании получили арксинусы, дальше подставили пределы интегрирования и округлили конечные значения.

ЗАДАНИЕ 4.4 Найти площадь плоской фигуры, которая образована кривыми:
x²+y²=2x, x²+y²=4x, y=x, y=0.
Решение: Начнем вычисление с анализа того, что собой представляет фигура, площадь которой нужно найти.
Сведем уравнения к простому виду
x²+y²=2x, x²-2x+1 +y²=1, (x-1)²+y²=1² - круг с центром в точке O₁(1;0) и радиусом R=1.
x²+y²=4x, x²-4x+4+y²=4, (x-2)²+y²=2² - круг с центром в точке O₁(2;0) и радиусом R=2.
y=x - прямая, которая является биссектрисой первой и третьей четверти. 
Рисунок к задаче илюстрирует площадь которой фигуры нужно найти

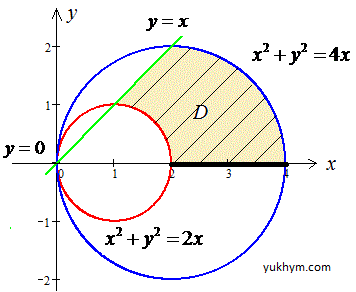
Поскольку поверхность ограничена кругами, то целесообразно перейти к полярным координатам.

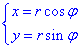
Найдем якобиан перехода:

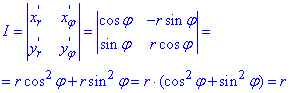
Запишем заданные функции в полярной системе координат:

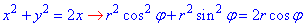
отсюда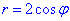

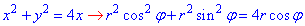
отсюда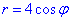
y=0, тогда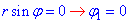
y=x, тогда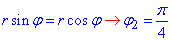
Это нам нужно, чтобы знать пределы в новой системе координат.
Пределы интегрирования в полярной системе координат:

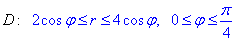
Вычислением кратного интеграла находим площадь фигуры, ограниченной заданными кривыми:

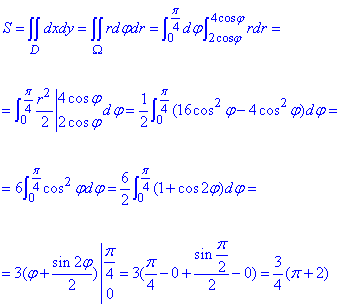
Конечное значение площади можно еще округлить.
Из этого примера Вы ознакомились как искать площадь в полярной системе координат.
В следующей статье разберем еще несколько примеров на нахождение площади фигур интегрированием.